
无约束现艾白的性质 af(x)af(x) af(x) 梯度→f()= ←列向量 0x1 0x2 梯度的特点:1)函数f)在X处增长最快的方向,负梯度方向 是函数f)在X处下降最快的方向;2)梯度的模是函数最快的 变化率;3)梯度为零是驻点,极值点是驻点,驻点不一定是极 值点。 o'f o'f o'f 海森(Hessian) 0x1 Ox 8x2 ox oxn 矩阵→ o'f o'f 2f ←方、对 f(X)=H(X)= x Ox2 2 Ox x0x 称矩阵 : 02f o'f o'f ox ox1 oxox
= = 2 2 2 2 1 2 2 2 2 2 2 1 2 2 1 2 1 2 2 2 1 2 2 ( ) ( ) n n n n n x f x x f x x f x x f x f x x f x x f x x f x f f X H X 无约束规划的性质 梯度→ T xn f X x f X x f X f X = ( ) , , ( ) , ( ) ( ) 1 2 列向量 梯度的特点:1) 函数f(X)在X处增长最快的方向,负梯度方向 是函数f(X)在X处下降最快的方向;2)梯度的模是函数最快的 变化率; 3) 梯度为零是驻点,极值点是驻点,驻点不一定是极 值点。 海森(Hessian) 矩阵→ 方、对 称矩阵

元约束规义树的性质 梯度为0向量的点可能是局部最优点,需要用海 森矩阵类型进一步判定; ●凸函数的驻点必是全局最优点; 补充)凶是凸函数←→对任意定义域D中的元素 X、Y和任意的数0sas1,有: faX+(1-0))≤f)+(1-M)f) 补充2)对称矩阵的分类 类别 A正定 A半正定 A负定 半负定 不定 定义 特征值>0 特征值≥0(有0) 特征值<0 特征值≤0(有0) 其它 判别方法 主子式都>0 A=0;主子式20 A正定 一A半正定
无约束规划的性质 ● 梯度为0向量的点可能是局部最优点,需要用海 森矩阵类型进一步判定; ● 凸函数的驻点必是全局最优点; 补充1) f(X)是凸函数→对任意定义域D中的元素 X、Y和任意的数0≤a≤1,有: f(aX+(1-a)Y) ≤af(X)+ (1-a) f(Y) 补充2) 对称矩阵的分类 类别 A正定 A半正定 A负定 半负定 不定 定义 特征值>0 特征值≥ 0(有0) 特征值<0 特征值≤0(有0) 其它 判别方法 主子式都>0 |A|=0;主子式≥ 0 -A正定 -A半正定
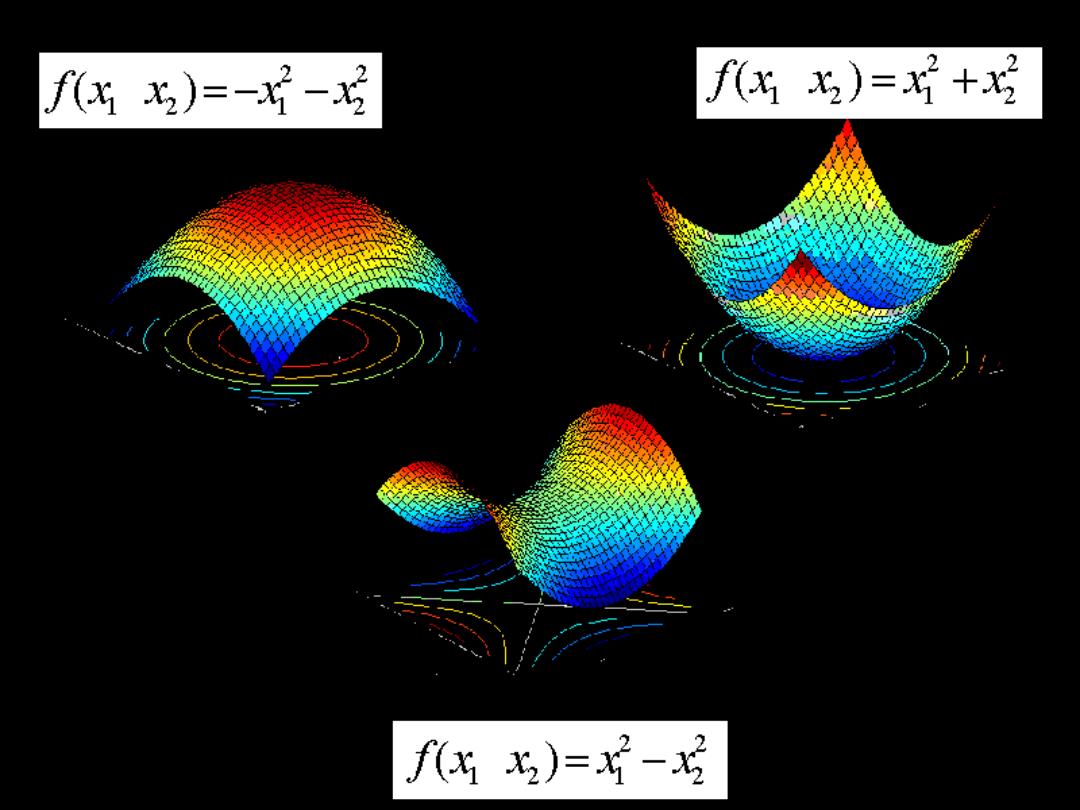
f出)=-片- f出)=x+ fx龙)=戈-写

无约束视文刻的甚本算法 基本思路:先求驻点,在判定是否是极值点; 基本方法一 迭代算法:先给定极小点的估计值 Sh+2 (初始值),寻求使函数值下降一个方向,沿此方 向找到一个更好的估计值,这样往复迭代,直到 某一点不能找到下降方向则终止算法. 迭代算法的基本框架: (1)选定初始点XW,令k=0: (2)在X处选定下降方向S(若找不到则终止算法); X+1 (3)从X出发沿Sf一维搜索,找到X+1=X+入S, 使得fX+)fX: (4)从k=k+1,转(2)
无约束规划的基本算法 基本思路:先求驻点,在判定是否是极值点; 基本方法——迭代算法: 先给定极小点的估计值 (初始值), 寻求使函数值下降一个方向, 沿此方 向找到一个更好的估计值, 这样往复迭代, 直到 某一点不能找到下降方向则终止算法. 迭代算法的基本框架: (1) 选定初始点X0 ,令k=0; (2)在Xk处选定下降方向S k (若找不到则终止算法); (3) 从Xk出发沿S k一维搜索, 找到Xk+1= Xk +λkS k , 使得 f(Xk+1)<f(Xk ); (4) 从k=k+1, 转(2). k X k+1 X k+2 X k+1 S k S k+2 S k k S

无约束规艾刘的基本算法 维搜索基本原则:)最优原则: 九:f(X*+九xS)=minf(X+S) 2>0 2)可接受点原则: 元:f(X*+2S)<fX) 一维搜索方法:0.618法、插值法等 下降方向:与梯度点乘为负值的方向 Vf(x).sk<0 (f(X+S)=f(x)+Vf(X)".S+olls<0
无约束规划的基本算法 一维搜索基本原则:1) 最优原则: 2) 可接受点原则: : ( ) min ( ) 0 k k k k k k f X S f X S + = + : ( ) ( ) k k k k k f X + S f X 一维搜索方法: 0.618法、插值法等 下降方向:与梯度点乘为负值的方向 ( ) 0 k T k f X S (f (X + S) = f (X) + f (X) S + o( S ) 0) T