华东理工学院：《线性代数》课程教学资源（PPT课件讲稿）第三章 矩阵的秩和线性代数方程组

初等变换求矩阵秩的方法： 把矩阵用初等行变换变成为行阶梯形矩阵， 行阶梯形矩阵中非零行的行数就是矩阵的秩 3 2 0 5 3 -2 3 6 -1 例4 设 A- 求矩阵A的 2 0 1 5 3 1 6 -4 -1 4 秩，并求A的一个最高阶非零子式： 解对A作初等行变换，了 变成阶梯形矩阵： 上页 返回

初等变换求矩阵秩的方法： 把矩阵用初等行变换变成为行阶梯形矩阵， 行阶梯形矩阵中非零行的行数就是矩阵的秩. 例4 秩，并求 的一个最高阶非零子式． 设 求矩阵 的 A A , A 1 6 4 1 4 2 0 1 5 3 3 2 3 6 1 3 2 0 5 0             − − − − − = 解 对A作初等行变换，变成行阶梯形矩阵：

2 0 -2 3 56 -1 A= 八 0 1 5 -3 6 4 6 -4 -1 4 3 -2 3 2 0 1 3 2 655 0 上页 下页 返回

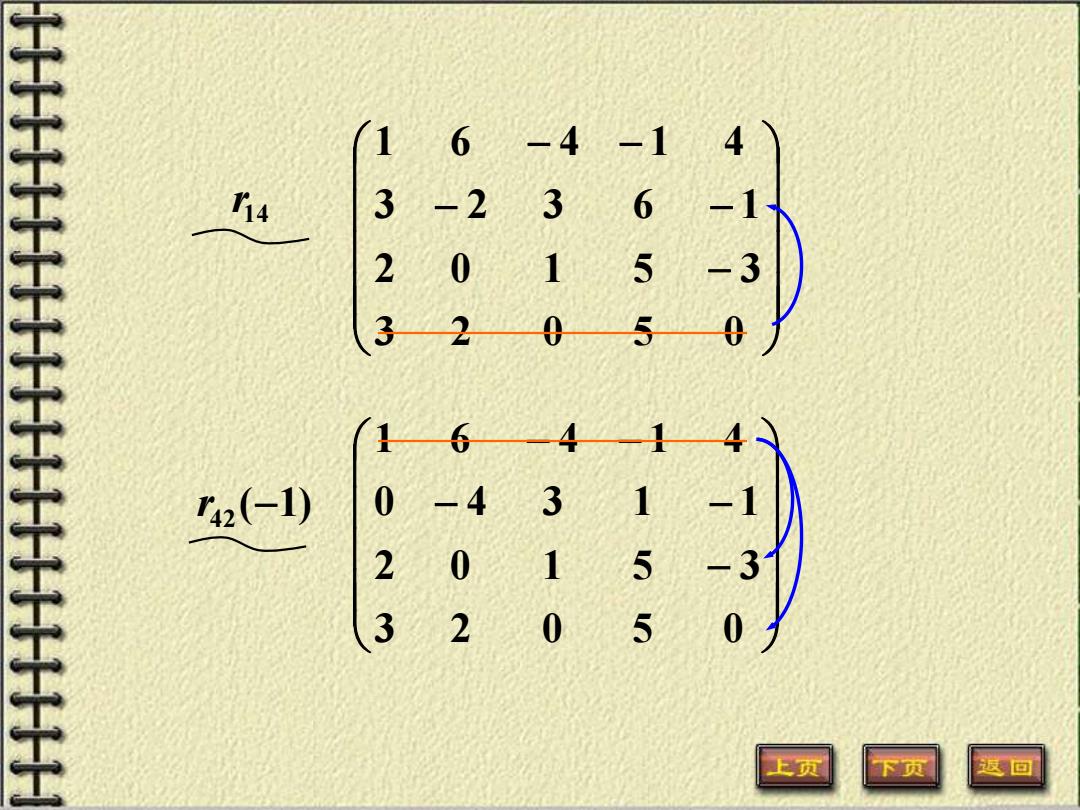
              − − − − − = 1 6 4 1 4 2 0 1 5 3 3 2 3 6 1 3 2 0 5 0 A               − − − − − 3 2 0 5 0 2 0 1 5 3 3 2 3 6 1 1 6 4 1 4 14 r

6 -4 -1 4 y -2 3 6 0 1 3 2 55 6 4 0 -4 3 1 3 1 3 02 0 55 30 上页 下页 返回

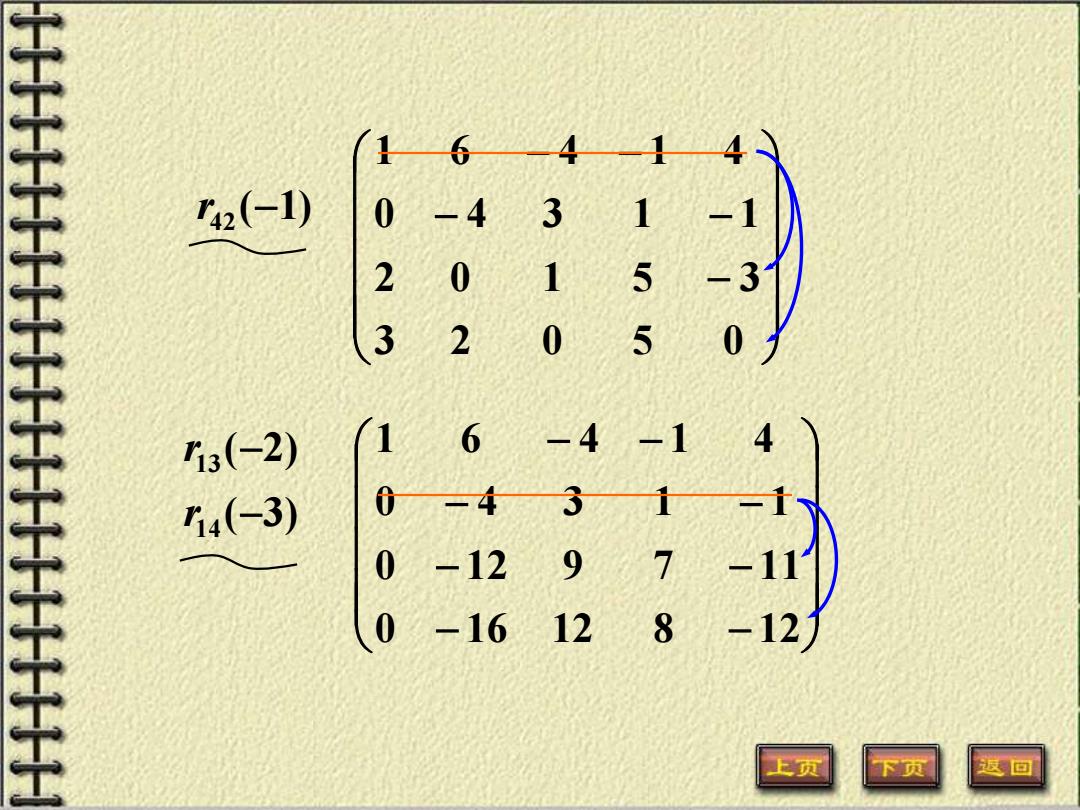
              − − − − − 3 2 0 5 0 2 0 1 5 3 0 4 3 1 1 1 6 4 1 4 ( 1) r42 −               − − − − − 3 2 0 5 0 2 0 1 5 3 3 2 3 6 1 1 6 4 1 4 14 r

6 414 0 -4 31 23 0 1 2 0 55 0 13(-2) 6 -4 -1 4 14(-3) 0 -431 0 -12 97 0 -16 128 上页 返回

              − − − − − − − − 0 16 12 8 12 0 12 9 7 11 0 4 3 1 1 1 6 4 1 4 ( 3) ( 2) 14 13 − − r r               − − − − − 3 2 0 5 0 2 0 1 5 3 0 4 3 1 1 1 6 4 1 4 ( 1) r42 −

13(-2) 16 -4-1 4 14(-3) 0-43 0 -12 97 0 -16 12 8 1 6 -4-1 0 -43 1 0 0 0 8 0 0 0 4 上页 下页 返回

              − − − − − − − − 0 16 12 8 12 0 12 9 7 11 0 4 3 1 1 1 6 4 1 4 ( 3) ( 2) 14 13 − − r r               − − − − − − 0 0 0 4 8 0 0 0 4 8 0 4 3 1 1 1 6 4 1 4 ( 3) r23 − ( 4) r24 −