
由于C在[0,+o)上只有一个极大值点,且t→+∞ 时,c→0。 所以1=-na时,C达到最大值 02-01 01 02-01 即当时间t= lno2-lnC1时,血药浓 02-01 01 01 02-1 度为最大,其最大浓度为口 2 02 四、函数曲线的凹凸性和拐点 1.概念 定义2-4设函数y=f(x)在[a,b]上连续,如果对于 [a,b]上的任意两点x,x2,有 8
8 由 于C 在[0, ) + 上只有一个极大值点,且t → + 时,c → 0。 所 以 2 1 2 1 ln ln t − = − 时 , C 达 到 最 大 值 1 2 1 1 max 2 2 A C − = 。即当时间 2 1 2 1 ln ln t − = − 时,血药浓 度为最大,其最大浓度为 1 2 1 1 2 2 A − 。 四、函数曲线的凹凸性和拐点 1.概念 定 义 2-4 设函数 y f x = ( )在[ , ] a b 上连续,如果对于 [ , ] a b 上的任意两点 1 2 x x, ,有
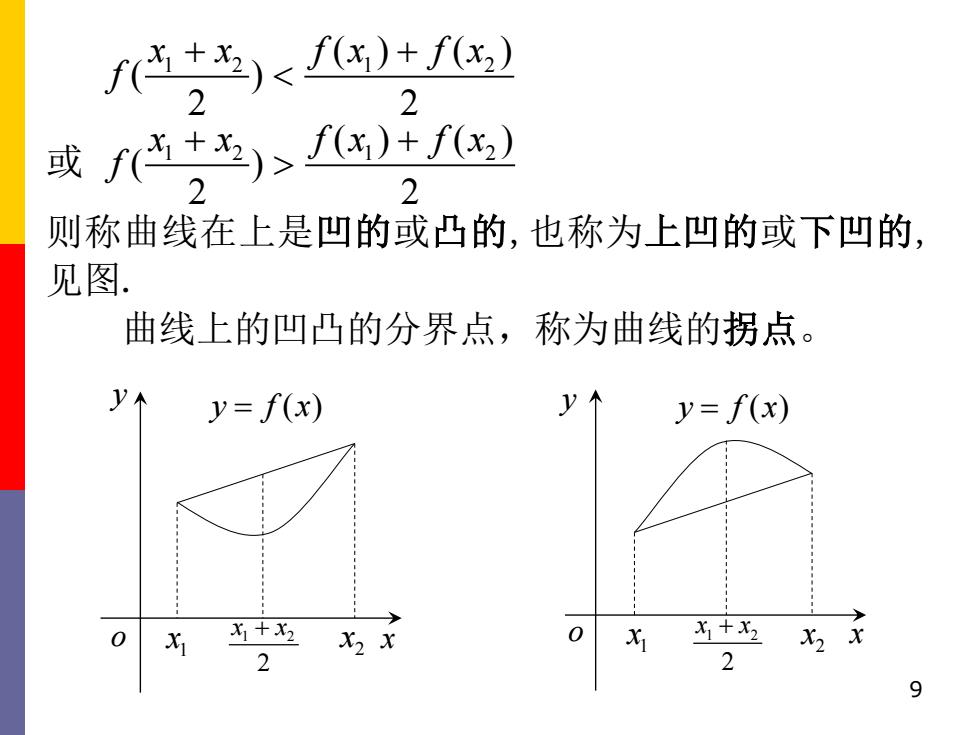
f)<f)+f 2 2 或f(+)>fx)+f) 2 则称曲线在上是凹的或凸的,也称为上凹的或下凹的, 见图. 曲线上的凹凸的分界点,称为曲线的拐点。 y=f(x) y=f(x) X 为十 X2 X X+x2 X2 x 2 2 9
9 1 2 1 2 ( ) ( ) ( ) 2 2 x x f x f x f + + 或 1 2 1 2 ( ) ( ) ( ) 2 2 x x f x f x f + + 则称曲线在上是凹 的或凸 的,也称为上凹的或下凹的, 见图. 曲线上的凹凸的分界点,称为曲线的拐点。 1 2 2 x x + y o x 1 x 2 x y f x = ( ) y o x 1 x 2 1 2 x 2 x x + y f x = ( )

2.凹凸性的判别法 定理2-10设函数y=f(x)在(a,b)内具有二阶导数f"(x), 则有 ①若对任意x∈(a,b),有f"(x)>0,则曲线f(x)在(a,b) 内是凹的: ②若对任意x∈(a,b),有f"(x)<0,则曲线f(x)在 (a,b)内是凸的: 例1.判别曲线f(x)=lnx的凹凸性。 解 函数f(x)=lnx定义域为(0,+o), /)-子)-<0. 10
10 2.凹凸性的判别法 定理2-10 设函数y f x = ( )在( , ) a b 内具有二阶导数 f x ( ), 则有 ①若对任意x a b ( , ),有 f x ( ) 0 ,则曲线 f x( )在( , ) a b 内是凹的; ②若对任意 x a b ( , ),有 f x ( ) 0 ,则曲线 f x( )在 ( , ) a b 内是凸的; 例 1.判别曲线 f x x ( ) ln = 的凹凸性。 解 函数 f x x ( ) ln = 定义域为(0, ) + , 1 f x( ) x = , 2 1 f x( ) 0 x = −