南京大学：《离散数学 Discrete Mathmatics》课程教学资源（课件讲稿，2018）代数系统——第19章 代数格

格的代数性质 结合律 交换律 吸收律 幂等律 吸收律 !幂等律 xAx=xA(xVK)=x(两次应用吸收律) 同理可证：xVx=x 6

格的代数性质 结合律 交换律 吸收律 幂等律 吸收律 幂等律 x  x = x  ( x  (xx) ) = x （两次应用吸收律） 同理可证：x  x = x 6

关于格的对偶命题 。对偶命题的例子 ·aAb≤a和vb≥a互为对偶命题 ·对偶命题构成规律 。格元素名不变 。≤与产，A与v全部互换

关于格的对偶命题  对偶命题的例子  ab≼a和ab≽a互为对偶命题  对偶命题构成规律  格元素名不变  ≼与≽，与全部互换。 7

格的对偶原理 ·如果命题P对一切格为真，则P的对偶命题P*也对 一切格为真。 。证明思路：证明P对任意格(S,≤)为真 ·定义S上的二元关系≤*，Va,b∈S,a≤*b台b≤4，显然≤* 是偏序。 ●a,b∈S,aA*b=vb,aV*b=aAb所以(S,≤*)也是格 。这里aA*b,v*b分别是，b关于偏序<*的最大下界和最小上界。 ·P*在(S,)中为真当且仅当P在(S,≤*)中为真。 。P在一切格中为真，P*在一切格中为真。 8

格的对偶原理  如果命题P对一切格为真，则P的对偶命题P*也对 一切格为真。  证明思路：证明P*对任意格(S, ≼)为真  定义S上的二元关系≼* , a,bS, a≼*b  b≼a, 显然≼* 是偏序。  a,bS, a*b=ab, a*b=ab 所以(S, ≼*)也是格  这里a*b, a*b分别是a,b关于偏序≼*的最大下界和最小上界。  P*在(S, ≼)中为真当且仅当 P在(S, ≼*)中为真。  P在一切格中为真，P*在一切格中为真。 8

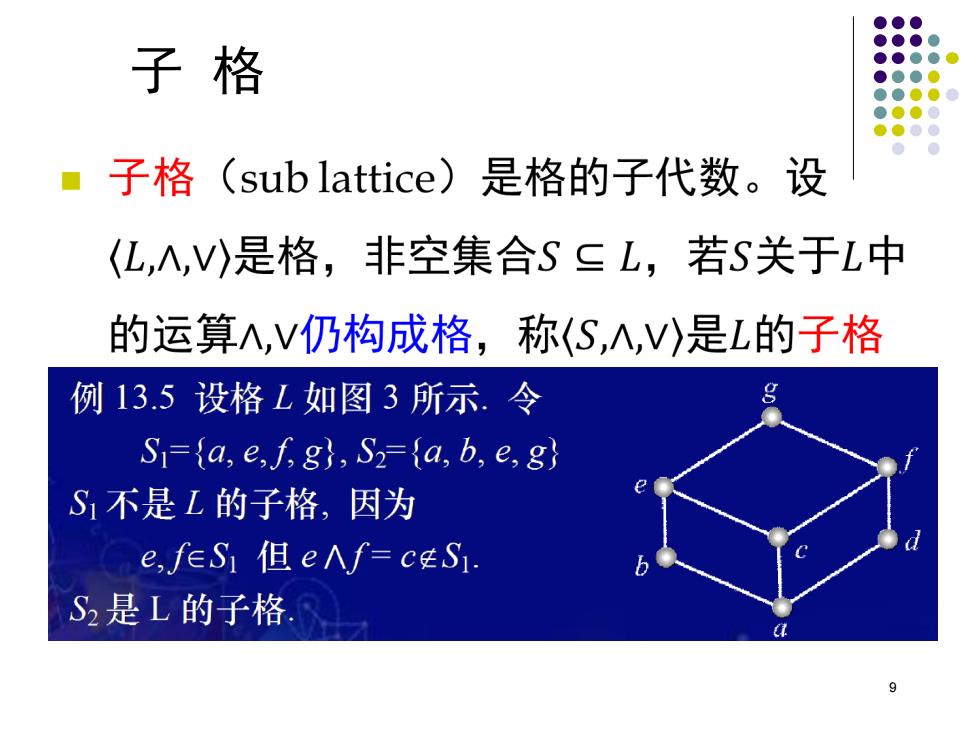
子格 ▣子格 (sub lattice)是格的子代数。设 (L,∧，V)是格，非空集合S≤L,若S关于L中 的运算A,V仍构成格，称(S,A,V)是L的子格 例13.5设格L如图3所示.令 S=a,e,f,gh,S2-a,b,e,gy S不是L的子格，因为 e,feS1但e∧f=ceS S2是L的子格

子 格 9

格同态 定义13.5设L1和L2是格 fL1→L2, 若Va,bEL1有 a∧b)=a∧b), favb)=fa)vfb) 成立，则称f为格L1到L2的同态映射，简称格同态 10

格同态 10