
计数 南京大学离散数学教学组
计数 南京大学离散数学教学组

款雪扇 回顾 ·布尔函数 ·代数系统与布尔代数 ·作为有补分配格的布尔代数 ·布尔代数与逻辑电路
回顾 布尔函数 代数系统与布尔代数 作为有补分配格的布尔代数 布尔代数与逻辑电路

&食感 提要 ·集合计数 ·容斥原理 ●鸽笼原理 ·排列与组合
提要 集合计数 容斥原理 鸽笼原理 排列与组合

毁 集合用于分类 ING 将属于某个集合的元素理 解为“具有某种性质”的 E F 对象,则属于该集合的补 集的元素则是“不具有某 EOF 种性质”的对象。 例如: 将全班同学的集合视为全集。 其子集E是学英语的同学的集 合,或理解为满足性质E的对 既学英语,又学法语的同学 象的集合。类似地,F是学法 语的同学的集合,即满足性质 F的对象的集合
集合用于分类 既学英语,又学法语的同学 E F EF 将属于某个集合的元素理 解为“具有某种性质”的 对象,则属于该集合的补 集的元素则是“不具有某 种性质”的对象。 例如: 将全班同学的集合视为全集。 其子集E是学英语的同学的集 合,或理解为满足性质E的对 象的集合。类似地,F是学法 语的同学的集合,即满足性质 F的对象的集合
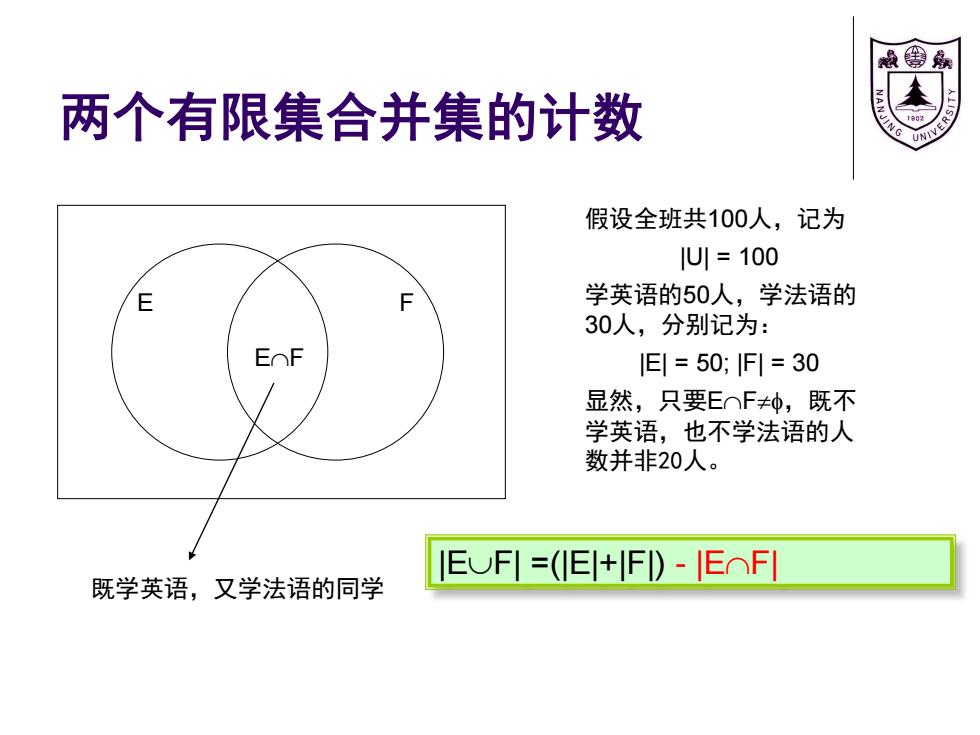
两个有限集合并集的计数 假设全班共100人,记为 U1=100 F 学英语的50人,学法语的 30人,分别记为: E=50;F1=30 显然,只要E⌒F≠种,既不 学英语,也不学法语的人 数并非20人。 IEUFI=(IE+FI)-JEOFI 既学英语,又学法语的同学
两个有限集合并集的计数 既学英语,又学法语的同学 E F EF 假设全班共100人,记为 |U| = 100 学英语的50人,学法语的 30人,分别记为: |E| = 50; |F| = 30 显然,只要EF,既不 学英语,也不学法语的人 数并非20人。 |EF| =(|E|+|F|) - |EF|