南京大学：《离散数学 Discrete Mathmatics》课程教学资源（课件讲稿，2018）图论——第26章 树的基本概念

树的基本概念 离散数学一树 南京大学计算机科学与技术系

树的基本概念 离散数学─树 南京大学计算机科学与技术系

殼壁嘉 内容提要 。树的定义 ·树的性质 ·根树 ·有序根树的遍历

内容提要  树的定义  树的性质  根树  有序根树的遍历

线兔 树的定义 ·定义：不包含简单回路的连通无向图称为树。 ●森林（连通分支为树) 。树叶/分支点（度为1？) 互不同构的6个顶点的树

树的定义  定义：不包含简单回路的连通无向图称为树。  森林（连通分支为树）  树叶/分支点（度为1？） 互不同构的6个顶点的树

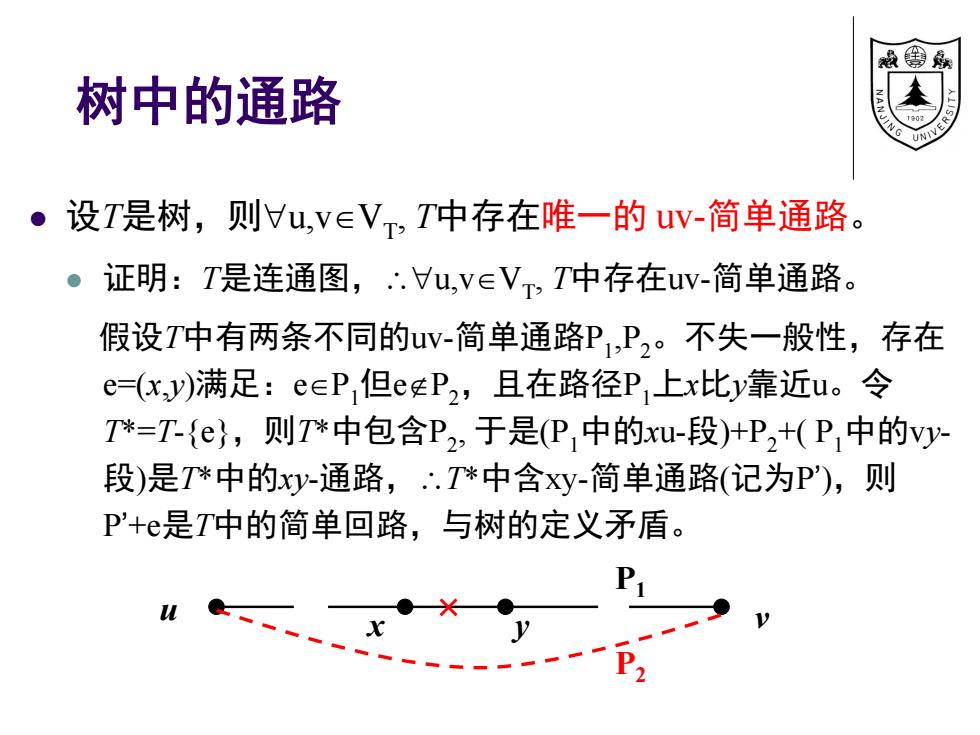
校线 树中的通路 ·设T是树，则u,V∈VT,T中存在唯一的uV-简单通路。 .7 证明：T是连通图，.u,v∈V,T中存在uv-简单通路。 假设T中有两条不同的uv-简单通路P,P2。不失一般性，存在 e=(x,y)满足：e∈P1但eEP2,且在路径P,上x比y靠近u。令 T*=T-{e},则T*中包含P,于是(P中的xu-段)+P2+(P中的vy 段)是T*中的xy-通路，∴.T*中含xy-简单通路（记为P),则 P'+e是T中的简单回路，与树的定义矛盾。 Pi P2

树中的通路  设T是树，则u,vVT , T中存在唯一的 uv-简单通路。  证明：T是连通图，u,vVT , T中存在uv-简单通路。 假设T中有两条不同的uv-简单通路P1 ,P2。不失一般性，存在 e=(x,y)满足：eP1但eP2，且在路径P1上x比y靠近u。令 T*=T-{e}，则T*中包含P2 , 于是(P1中的xu-段)+P2 +( P1中的vy- 段)是T*中的xy-通路，T*中含xy-简单通路(记为P’)，则 P’+e是T中的简单回路，与树的定义矛盾。 u x y v  P2 P1

急售扇 有关树的几个等价命题 ·设T是简单无向图，下列四个命题等价： (1)T是不包含简单回路的连通图。/树的定义 (2)T中任意两点之间有唯一简单通路。 (3)T连通，但删除任意一条边则不再连通。 (4)T不包含简单回路，但在任意不相邻的顶点对之间加一 条边则产生唯一的简单回路。 ●备注： ●树是边最少的连通图 ●树是边最多的无简单回路的图

有关树的几个等价命题  设T是简单无向图，下列四个命题等价： (1) T是不包含简单回路的连通图。//树的定义 (2) T中任意两点之间有唯一简单通路。 (3) T连通，但删除任意一条边则不再连通。 (4) T不包含简单回路，但在任意不相邻的顶点对之间加一 条边则产生唯一的简单回路。  备注：  树是边最少的连通图  树是边最多的无简单回路的图