
10.4细导线的线积分方程 1966 两个著名的求解细线的基本方程 当微分算子在积分符号外,可得到Hallen积分方程 (28) 当微分算子在积分符号内,可得到Pocklington积分方程 e dz (29) 4πr Q:从方程形式上看,哪一个方程MoM求解更困难?为什么? 7
7 10.4 细导线的线积分方程 当微分算子在积分符号外,可得到Hallen积分方程 ( ) ( ) 2 j i 2 2 2 2 j e ' d ' 4 L kr E z k I z z z z L z r − − = + 两个著名的求解细线的基本方程 当微分算子在积分符号内,可得到Pocklington积分方程 ( ) ( ) 2 j i 2 2 2 2 j e ' d ' 4 L kr E z I z k z z z L z r − − = + (28) (29) Q:从方程形式上看,哪一个方程MoM求解更困难?为什么?
10.4细导线的线积分方程 1966 10.4.2细线天线的激励源 天线的关键参数:输入阻抗(频率)、方向图、增益 建立馈源目的:不对馈线本身模型进行考虑 Delta:缝隙激励源(振子天线) 单位电压 激励电场施加在天线缝隙处: 2 E(e)= △zE △z 缝隙的宽度 >激励场只在一个分段区域中存在 >优点:实施简单、计算方向图准确 >缺点:但计算输入阻抗的精度稍差 2a 8
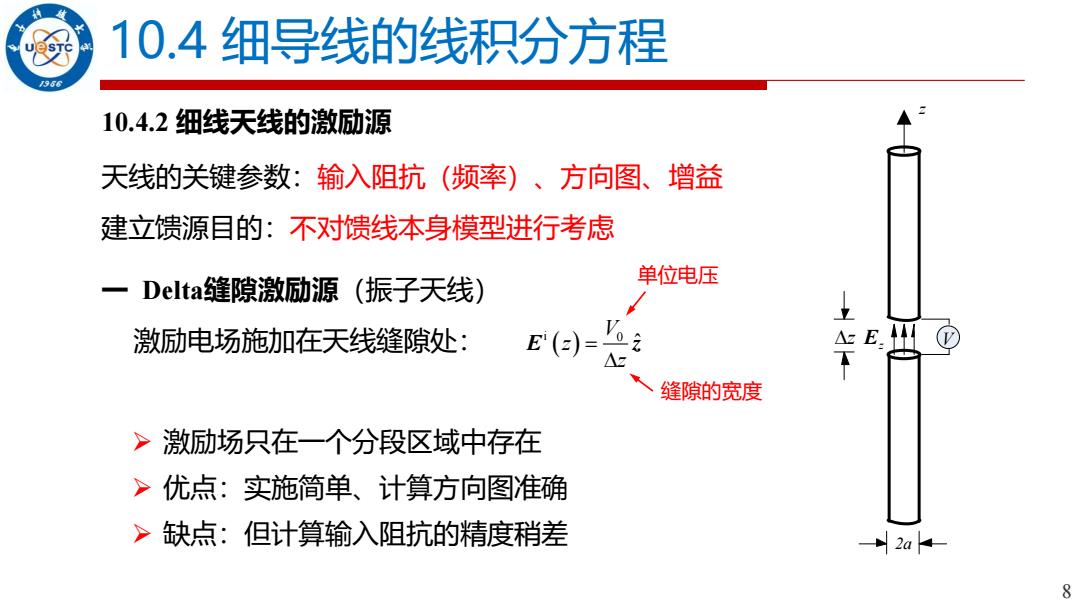
8 10.4 细导线的线积分方程 10.4.2 细线天线的激励源 一 Delta缝隙激励源(振子天线) z 2a E z z V 天线的关键参数:输入阻抗(频率)、方向图、增益 建立馈源目的:不对馈线本身模型进行考虑 激励电场施加在天线缝隙处: ( ) i 0 ˆ V z z = E z 单位电压 缝隙的宽度 ➢ 激励场只在一个分段区域中存在 ➢ 优点:实施简单、计算方向图准确 ➢ 缺点:但计算输入阻抗的精度稍差