
Chapter 6 Architecture and Equilibria 结构和平衡 学生:郑巍 导师:刘三阳
Architecture and Equilibria 结构和平衡 学生:郑巍 导师:刘三阳 Chapter 6

Chapter 6 Architecture and Equilibria 6.1 Neutral Network As Stochastic Gradient system Classify Neutral network model By their synaptic connection topologies and by how learning modifies their connection topologies synaptic connection topologies (1.feedforward.if No closed synaptic loops 2.feedback if closed synapticloops orfeedback pathways how learning modifies their connection topologies 1.Supervised learning:use class-membership information of training samplings 2.Unsupervised learning:use unlabelled training samplings 2006.11.10 2
2006.11.10 2 Chapter 6 Architecture and Equilibria 6.1 Neutral Network As Stochastic Gradient system Classify Neutral network model By their synaptic connection topologies and by how learning modifies their connection topologies feedback i f closed synapticloops orfeedback pathways feedforward i f No closed synaptic loops 2. . 1. . 1. : 2. : Supervised learning use class membership information of training samplings Unsupervised learning use unlabelled training samplings − synaptic connection topologies how learning modifies their connection topologies
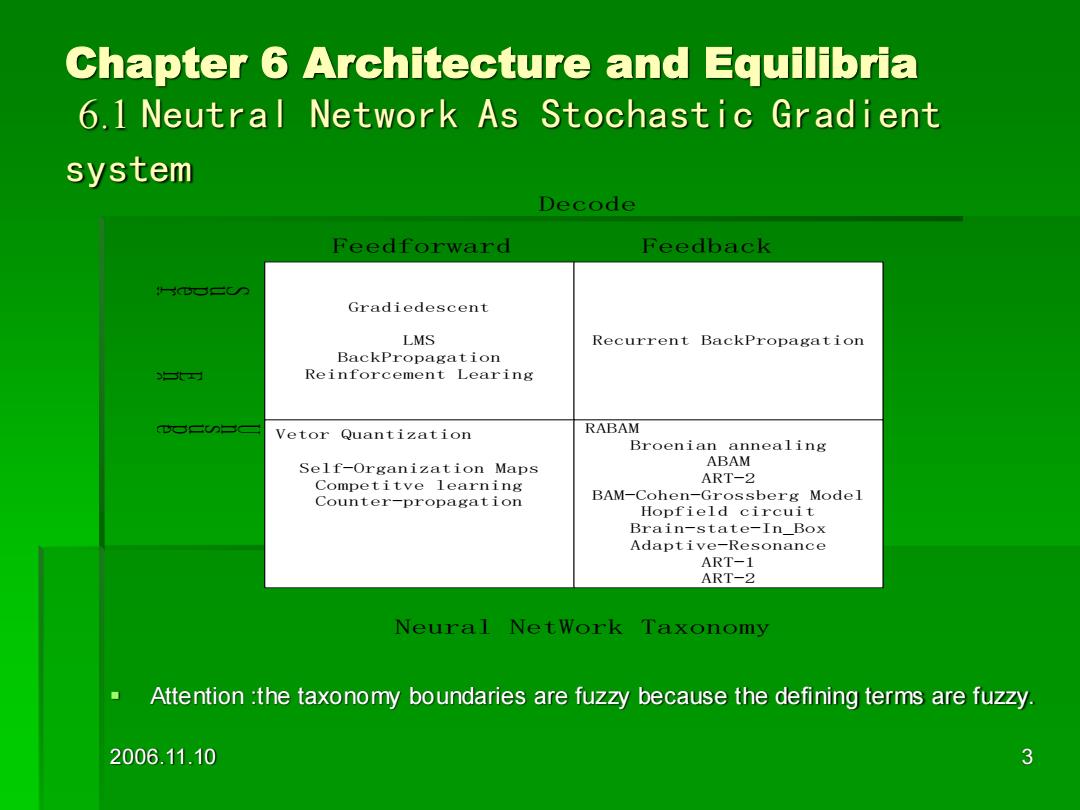
Chapter 6 Architecture and Equilibria 6.1 Neutral Network As Stochastic Gradient system Decode Feedforward Feedback s口二 Gradiedescent LMS Recurrent BackPropagation BackPropagation 1 Reinforcement Learing Vetor Quantization RABAM Broenian annealing Self-Organization Maps ABAM Competitve learning ART-2 Counter-propagation BAM-Cohen-Grossberg Model Hopfield circuit Brain-state-In_Box Adaptive-Resonance ART-1 ART-2 Neural NetWork Taxonomy Attention the taxonomy boundaries are fuzzy because the defining terms are fuzzy. 2006.11.10 3
2006.11.10 3 Chapter 6 Architecture and Equilibria 6.1 Neutral Network As Stochastic Gradient system ▪ Attention :the taxonomy boundaries are fuzzy because the defining terms are fuzzy. Gradiedescent LMS BackPropagation Reinforcement Learing Recurrent BackPropagation Vetor Quantization Self-Organization Maps Competitve learning Counter-propagation RABAM Broenian annealing ABAM ART-2 BAM-Cohen-Grossberg Model Hopfield circuit Brain-state-In_Box Adaptive-Resonance ART-1 ART-2 Feedforward Feedback Decode d e s i v r e p u S d e s i v r e p u s n U e d o c n E Neural NetWork Taxonomy

Chapter 6 Architecture and Equilibria 6.1 Neutral Network As Stochastic Gradient system Three stochastic gradient systems represent the three main categories 1 Backpropagation (BP) 2 Adaptive vector quantization (AVQ) 3 Random adaptive bidirectional associative memory (RABAM) 2006.11.10 4
2006.11.10 4 Chapter 6 Architecture and Equilibria 6.1 Neutral Network As Stochastic Gradient system ▪ Three stochastic gradient systems represent the three main categories 1 Backpropagation (BP) 2 Adaptive vector quantization (AVQ) 3 Random adaptive bidirectional associative memory (RABAM)

Chapter 6 Architecture and Equilibria 6.2 Global Equilibria:convergence and stability Neural network synapses neurons three dynamical systems synapses dynamical systems M neurons dynamical systems X joint synapses-neurons dynamical systems (X.M) Historically,Neural engineers study the first or second neural network independently.They usually study learning in feedforward neural networks and neural stability in nonadaptive feedback neural networks.RABAM and ART network depend on joint equilibration of the synaptic and n2081a9 dynamical systems. 5
2006.11.10 5 Chapter 6 Architecture and Equilibria 6.2 Global Equilibria: convergence and stability Neural network :synapses , neurons three dynamical systems synapses dynamical systems neurons dynamical systems joint synapses-neurons dynamical systems Historically,Neural engineers study the first or second neural network independently .They usually study learning in feedforward neural networks and neural stability in nonadaptive feedback neural networks. RABAM and ART network depend on joint equilibration of the synaptic and neuronal dynamical systems. ' M ' X ( , ) ' ' X M