
模糊与卡尔曼滤波目标跟踪控制系统的比较 Comparison of Fuzzy and Kalman-Filter Target-Tracking control system Peter J.Pacini,Bart Kosko 导师:吴顺君 教授 学生: 胡亮兵
模糊与卡尔曼滤波目标跟踪控制系统的比较 Comparison of Fuzzy and Kalman-Filter Target-Tracking control system 导 师:吴顺君 教授 学 生:胡亮兵 Peter J.Pacini , Bart Kosko

内容简介 1、模糊控制器与卡尔曼滤彼器的比放 2、实时目标跟踪系统 3、模糊控制器的工作原程 4、卡尔曼滤被跟踪与模糊跟踪的伤真 5、省百适应FAM
1、模糊控制器与卡尔曼滤波器的比较 3、模糊控制器的工作原理 2、实时目标跟踪系统 内容简介 5、自适应FAM 4、卡尔曼滤波跟踪与模糊跟踪的仿真

1、模糊控制器与卡尔曼滤波器的比较 卡尔曼滤波器需要 模糊控制器是 明确的数学模型来定义 一个模糊系统, 输出与输入之间的关系 其输出与输入之 X6=ΦA-XA+「kUA1+W 间没有经典的数 学模型 。 ZR=HkXk+VR 通过测量估计真实代价(最小 均方误差)》 递推
1、模糊控制器与卡尔曼滤波器的比较 卡尔曼滤波器需要 明确的数学模型来定义 输出与输入之间的关系 模糊控制器是 一个模糊系统, 其输出与输入之 间没有经典的数 , −1 −1 , −1 −1 −1 学模型。 Xk = k k Xk + k k Uk +Wk Zk = Hk Xk +Vk 通过测量估计真实 代价(最小 均方误差) 递推
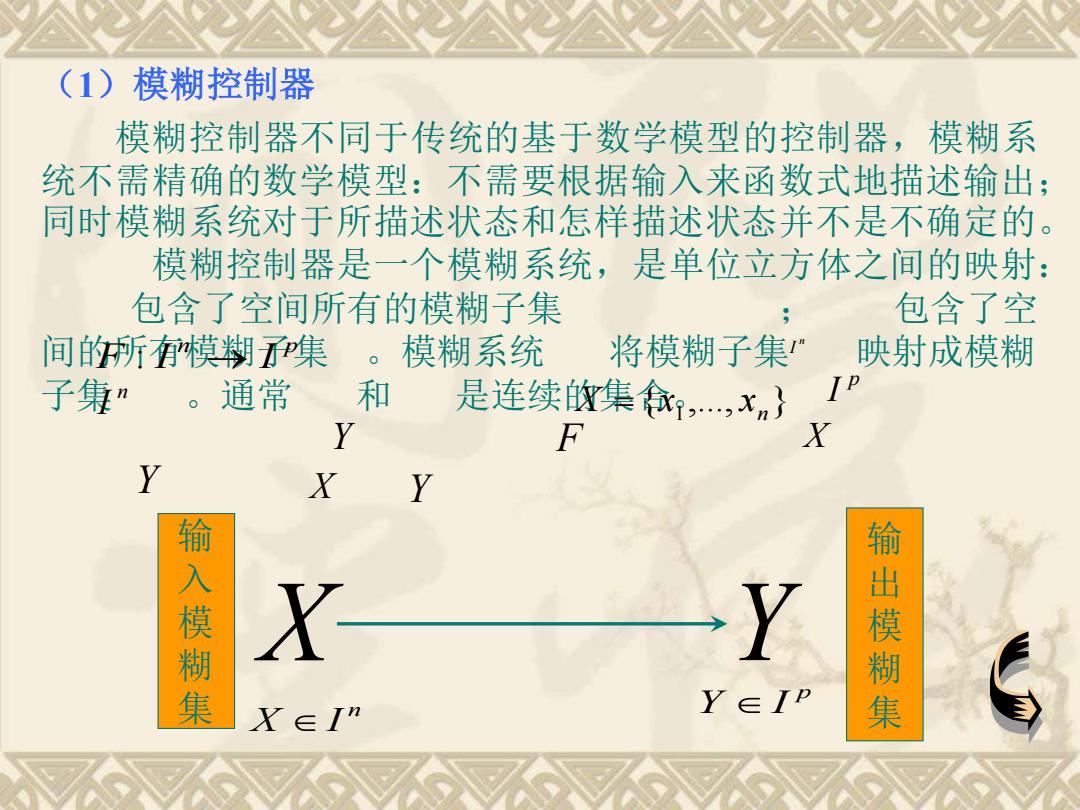
(1)模糊控制器 模糊控制器不同于传统的基于数学模型的控制器,模糊系 统不需精确的数学模型:不需要根据输入来函数式地描述输出; 同时模糊系统对于所描述状态和怎样描述状态并不是不确定的。 模糊控制器是一个模糊系统,是单位立方体之间的映射: 包含了空间所有的模糊子集 包含了空 间的所有模糊集。模糊系统 将模糊子集 映射成模糊 子集”。通常 和 是连续的集,,xn} Y F X X Y 输入 模糊集 X 输出模糊集 X∈I” Y∈IP
n I (1)模糊控制器 X 模糊控制器不同于传统的基于数学模型的控制器,模糊系 统不需精确的数学模型:不需要根据输入来函数式地描述输出; 同时模糊系统对于所描述状态和怎样描述状态并不是不确定的。 模糊控制器是一个模糊系统,是单位立方体之间的映射: 包含了空间所有的模糊子集 ; 包含了空 间的所有模糊子集 。模糊系统 将模糊子集 映射成模糊 子集 。通常 和 是连续的集合。 n p F : I → I { ,..., } 1 n X = x x p I F X Y Y Y n I X Y n X I p Y I 输 入 模 糊 集 输 出 模 糊 集

模糊控制器有一系列的FAM(模糊自联想记忆) “规则”,它描述模糊的专家知识或学习训练好的输 入到输出的转换。一个FAM可以总结概括一个特定的 数学模型的动作。模糊系统可以非线性地将一个确定 的或模糊化的输入转变成一个模糊集输出。这个输出 模糊集通过质心化(“去模糊”)可得到一个具体的 数值。模糊控制器需要我们说明或估计出FAM规则。 虽然模糊控制器是一个数字化的系统,但专家可以将 他的知识用自然语言总结,这一点对于复杂问题具有 重要的意义
模糊控制器有一系列的FAM(模糊自联想记忆) “规则”,它描述模糊的专家知识或学习训练好的输 入到输出的转换。一个FAM可以总结概括一个特定的 数学模型的动作。模糊系统可以非线性地将一个确定 的或模糊化的输入转变成一个模糊集输出。这个输出 模糊集通过质心化(“去模糊”)可得到一个具体的 数值。模糊控制器需要我们说明或估计出FAM规则。 虽然模糊控制器是一个数字化的系统,但专家可以将 他的知识用自然语言总结,这一点对于复杂问题具有 重要的意义