
NEURAL NETWORK THEORY NEURAL DYNAMIC1: ACTIVATIONHS AND SIGNALS
NEURAL NETWORK THEORY NEURAL DYNAMIC1: ACTIVATIONHS AND SIGNALS

MAIN POINTS: NEURONS AS FUNCTIONS(神经元函数) SIGNAL MONOTONICITY(信号单调性) BIOLOGICAL ACTIVATIONS AND SIGNALS(生物激 励与信号) NEURON FIELDS(神经域 NEURONAL DYNAMICAL SYSTEMS(神经诊断系统) COMMON SIGNAL FUNCTION(一般信号方程) PULSE-CODED SIGNAL FUNCTION(脉冲编码信号 方程)
MAIN POINTS: • NEURONS AS FUNCTIONS(神经元函数) • SIGNAL MONOTONICITY(信号单调性) • BIOLOGICAL ACTIVATIONS AND SIGNALS(生物激 励与信号) • NEURON FIELDS(神经域) • NEURONAL DYNAMICAL SYSTEMS(神经诊断系统) • COMMON SIGNAL FUNCTION(一般信号方程) • PULSE-CODED SIGNAL FUNCTION(脉冲编码信号 方程)
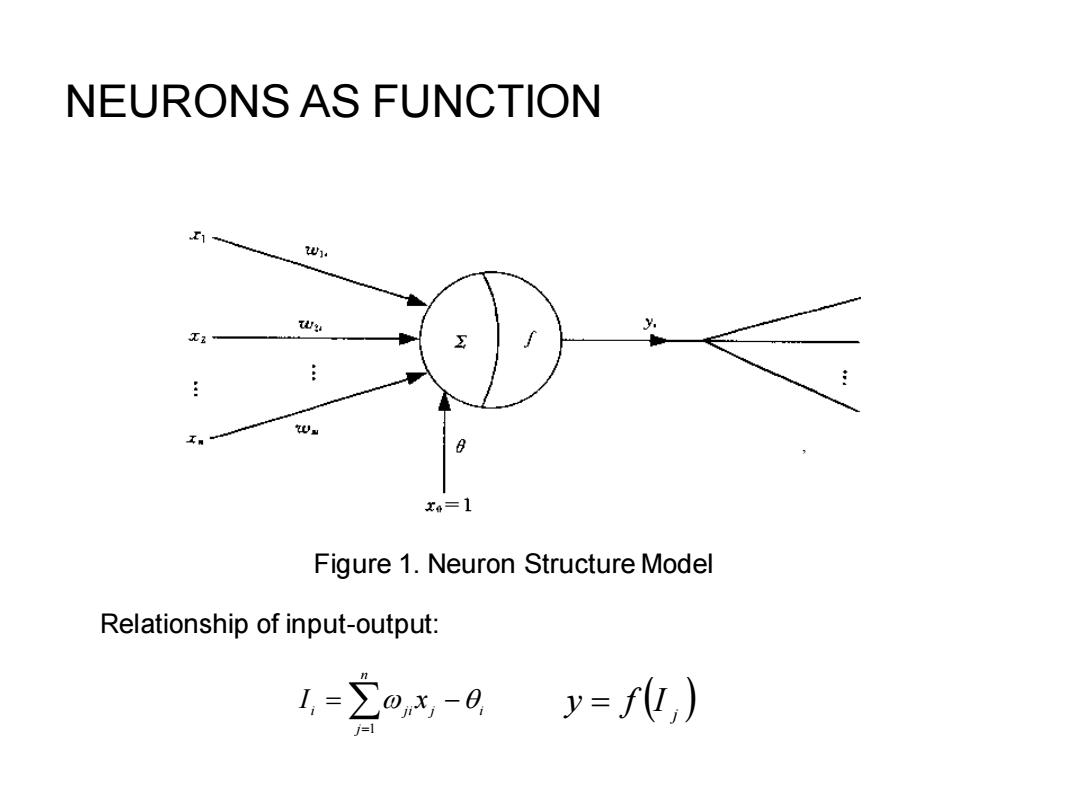
NEURONS AS FUNCTION w Wy x6=1 Figure 1.Neuron Structure Model Relationship of input-output: 1,=2o,x-日y=f,)
NEURONS AS FUNCTION Figure 1. Neuron Structure Model j i n j i ji I = x − =1 ( )j y = f I , Relationship of input-output:

NEURONS AS FUNCTION .Common nonlinear transduction description:a sigmoidal or S-shaped curve s(x) c=5.0 1.0 c=2.0 c=0.2 0 x Fig.2 s(x)is a bounded monotone-nondecreasing function of x Signal Function:S(x)= 1tea dS =cS(1-S)>0 dx (c>0) Neurons transduce an unbounded input activation x(t)at time t into a bounded output signal S(x(t))
•Common nonlinear transduction description: a sigmoidal or S-shaped curve Fig.2 s(x) is a bounded monotone-nondecreasing function of x Signal Function: cx e S x − + = 1 1 ( ) ' = = cS(1− S) 0 (c 0) dx dS S Neurons transduce an unbounded input activation x(t) at time t into a bounded output signal S(x(t)). NEURONS AS FUNCTION

SIGNAL MONOTONICITY In general,signal functions are monotone nondecreasing S'>=0.In practice this means signal functions have an upper bound or saturation value An important exception:bell-shaped signal function or Gaussian signal functions S(x)=e-r c>0 S=-2cxe S"oc-x The sign of the signal-activation derivation s'is opposite the sign of the activation x.We shall assume signal functions are monotone nondecreasing unless stated otherwise
SIGNAL MONOTONICITY ( ) 0 2 = − S x e c cx • In general, signal functions are monotone nondecreasing S’>=0. In practice this means signal functions have an upper bound or saturation value. • An important exception: bell-shaped signal function or Gaussian signal functions S cxe S x cx = − − − ' 2 , ' 2 The sign of the signal-activation derivation s’ is opposite the sign of the activation x. We shall assume signal functions are monotone nondecreasing unless stated otherwise