
模糊与概率(二) 刘新 2006.11.20
模糊与概率(二) 刘靳 2006.11.20

问题的提出 ◆如何表征模糊集合的模糊程度 模煳熵 ◆如何表征模糊集合间的包含关系 模糊包含度 ◆如何用模糊集合间的包含关系表征某个模 糊集合的模糊程度 模煳熵一包含度定理
问题的提出 ◆如何表征模糊集合的模糊程度 模糊熵 ◆如何表征模糊集合间的包含关系 模糊包含度 ◆如何用模糊集合间的包含关系表征某个模 糊集合的模糊程度 模糊熵—包含度定理
模糊集合的模糊程度模糊熵 任2}=(0) X=(11) 子 b 中=(00) }=(10) x: A的模糊熵E(A),在单位超立方体中从0到1,其中顶点的熵为0,表明不模糊, 中点的熵为1,是最大熵。从顶点到中点,熵逐渐增大。引出熵的比例形式: E(A)= 1'(A,Anear) 1(A,Aja) 1+1_7,b= A=(写.A=0,14m=10.a=3+412b= 2,317 7 412 E(=
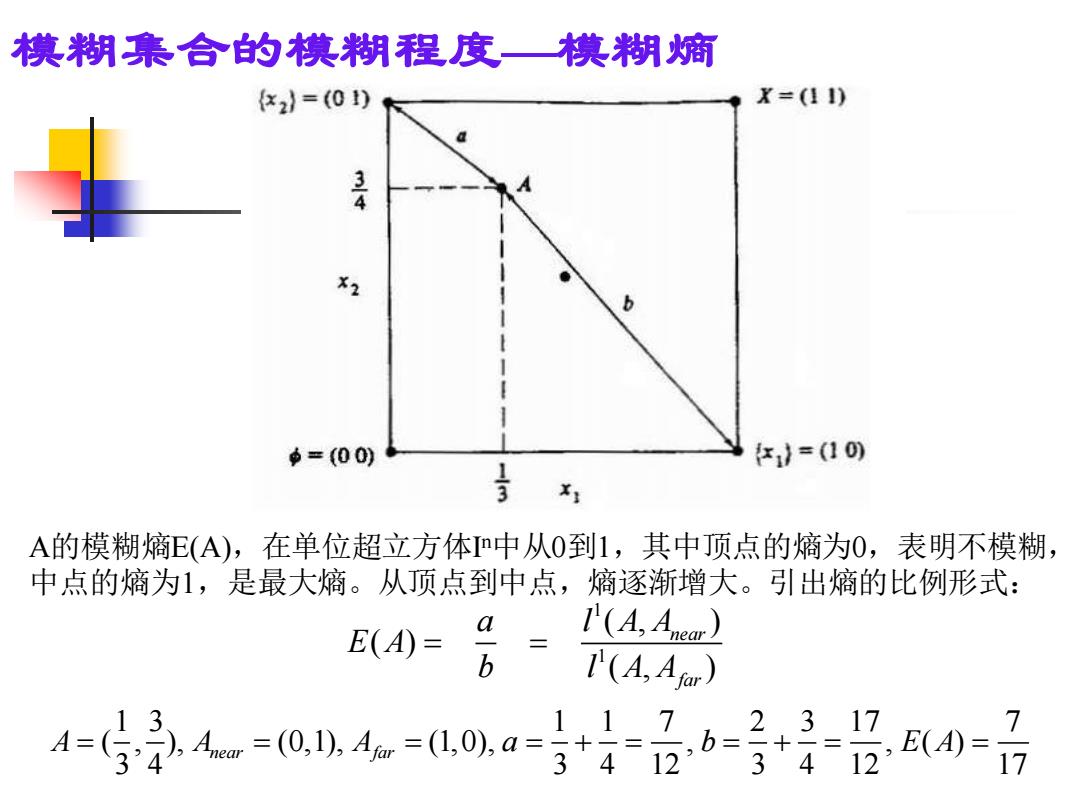
A的模糊熵E(A),在单位超立方体I n中从0到1,其中顶点的熵为0,表明不模糊, 中点的熵为1,是最大熵。从顶点到中点,熵逐渐增大。引出熵的比例形式: 1 1 ( , ) ( ) ( , ) near far a l A A E A b l A A = = 1 3 1 1 7 2 3 17 7 ( , ), (0,1), (1,0), , , ( ) 3 4 3 4 12 3 4 12 17 A A A a b E A = = = = + = = + = = near far 模糊集合的模糊程度—模糊熵
模糊集合的模糊程度模糊熵(续) {x2}=(01) X=(11) 模糊熵定理: X2 M(A⌒A) E(A M(A A∩AAE M(AUA) M(A 中=(00) {}=(10) 3 模糊熵定理的几何图示。由对称性,完整模糊方形的四个点到各 自的最近顶点、最远顶点的距离都相等。该定理正式宣告了“西 方逻辑”的终止。( M(A04)=0,M(A04)=n,E(A)=0
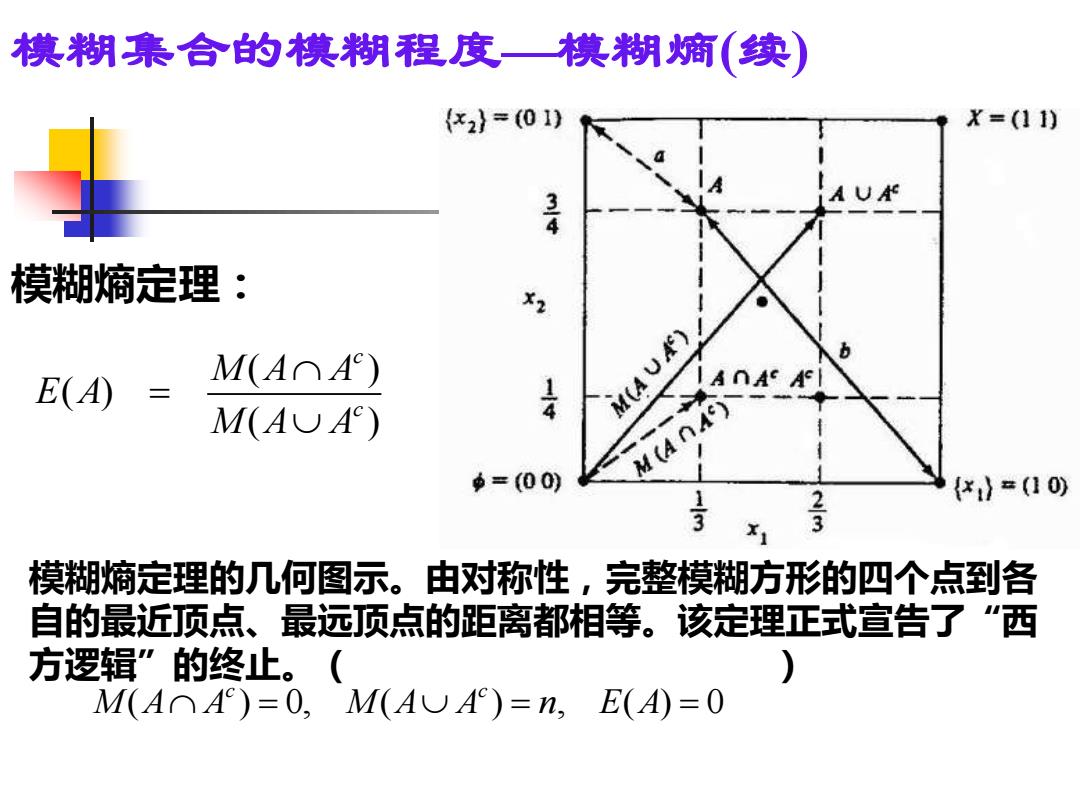
模糊熵定理: ( ) ( ) ( ) c c M A A E A M A A = 模糊熵定理的几何图示。由对称性,完整模糊方形的四个点到各 自的最近顶点、最远顶点的距离都相等。该定理正式宣告了“西 方逻辑”的终止。( ) ( ) 0, ( ) , ( ) 0 c c M A A M A A n E A = = = 模糊集合的模糊程度—模糊熵(续)

模糊集合间的包含关系一包含度定理 主导隶属度函数关系(dominated membership function relationship): AcB if and only if m(x)<mp(x)for all x 如果A=(.30.7)和B=(.4.7.9),那么A就是 B的一个模糊子集,但B不是A的模糊子集。显然 这种模糊包含度是非模糊的,它是非黑即白的, 是二值定义下的子集性(Zadeh's1965)
模糊集合间的包含关系—包含度定理 主导隶属度函数关系(dominated membership function relationship): ( ) ( ) A B if and only if m x m x for all x A B 如果A=(.3 0 .7)和B=(.4 .7 .9),那么A就是 B的一个模糊子集,但B不是A的模糊子集。显然, 这种模糊包含度是非模糊的,它是非黑即白的, 是二值定义下的子集性(Zadeh’s1965)