
△E=R1( n 当n=1,n2=o时,△E=2.179×10-18J, AE-the ionization energy of a hydrogen atom (氢原子的电离能) a证=yv-3289x105(日 3.289×1015=2.179×1018 h It can be seen that the meaning of the constant is the quotient of ionization energy divided by the Planck constant
) 1 1 ( 2 2 2 1 H n n E R h 1 8 1 5 2.179 10 3.289 10 ) 1 1 1 3.289 10 ( 2 2 1 5 E h E theionization energy of a hydrogen atom. 当n1 1,n2 时,E 2.179101 8J, (氢原子的电离能 ) the quotient of ionization energy divided by the Planck constant。 It can be seen that the meaning of the constant is

The difference in energy (AE)between energy levels n and c En=E-E,=m=hx3289x10- n202 2.179×1018 Eorbital energy of the n orbital for an electron Regulation(规定):(Eac=0) n一quantum number(量子数) En、 2.179×10-18 Calculation of energy of specified orbits of the H atom E.g:the transfer energy between 4th orbital and 2ed orbital: 5=6-6=2179103=408610 Hs 1=c=3.0x107 ↑ △E4.086×10-19 V= =486.5nm h 6.626×104=6.167×104 6.167×104
E E E hv n n -1 2 2 1 5 s 1 1 3.289 10 n h En—— orbital energy of the orbital for an electron n— quantum number (量子数) E.g: the transfer energy between 4th orbital and 2ed orbital: 1 4 1 3 4 1 9 6.167 10 6.626 10 4.086 10 s h E v 486.5nm 6.167 10 3.0 10 1 4 1 7 v c Hβ The difference in energy (En ) between energy levels n and Regulation(规定):(E= 0) Calculation of energy of specified orbits of the H atom J 2.179 10 2 18 n E E E J 19 2 2 18 4 2 ) 4.086 10 2 1 4 1 - 2.179 10 ( J 2.179 10 2 18 n En
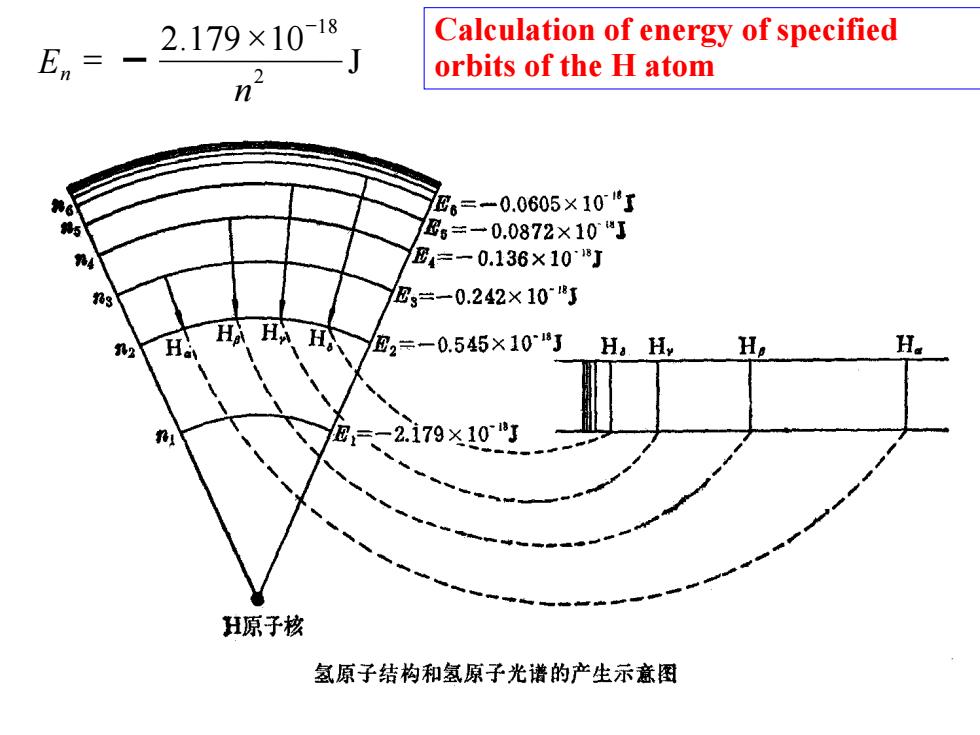
En、 2.179×1018 Calculation of energy of specified J orbits of the H atom n E6=-0.0605×10了 6=一0.0872×10J E4=一0.136×108J E3=一0.242×108J 2 H 、H,=-0.545×10" Ha H, H -2.179×10 H原子核 氢原子结构和氢原子光谱的产生示意图
J 2 .179 10 2 18 n E n Calculation of energy of specified orbits of the H atom
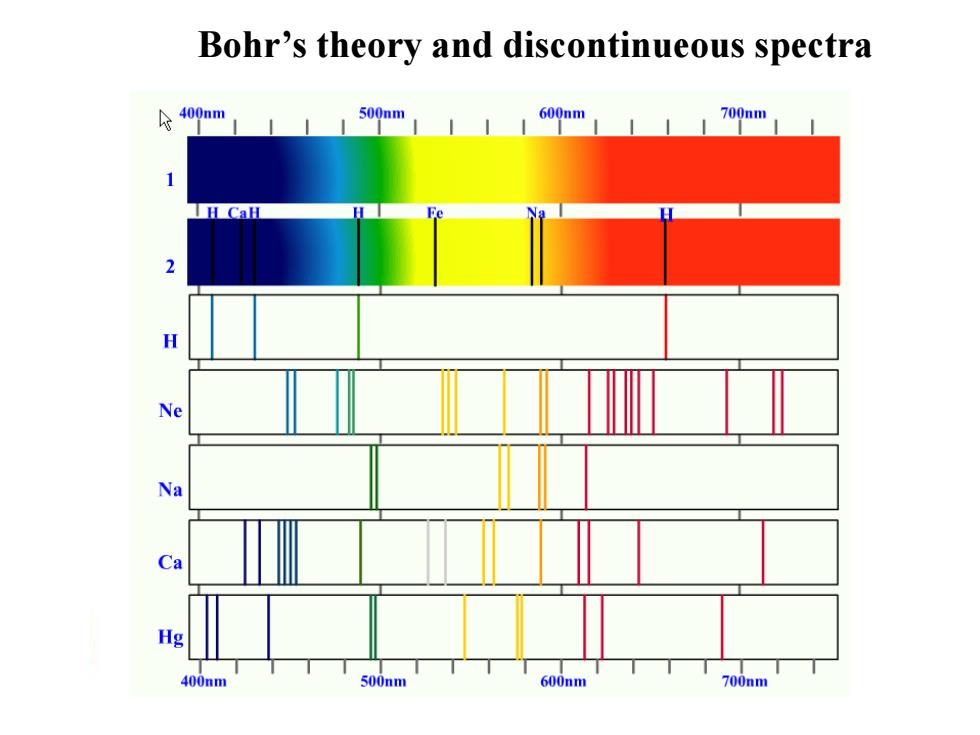
Bohr's theory and discontinueous spectra 个400nm 500nm 600nm 700nm g 400nm 500nm 600nm 700nm
Bohr’s theory and discontinueous spectra

5.1.2 The dual nature of the electron In 1925,Louis de Broglie proposed that a free moving electron with mass m and velocity o should have an associated wavelength given by the equation E=mc2=hr→=旅=名 h=6.626X 10-34Js,p,Planck's constant In 1927,an electron diffraction experiment with Ni crystal did by Davissson and Germerdid confirms the wave character of electron
In 1925, Louis de Broglie proposed that a free moving electron with mass m and velocity υ should have an associated wavelength given by the equation : 5.1.2 The dual nature of the electron In 1927, an electron diffraction experiment with Ni crystal did by Davissson and Germerdid confirms the wave character of electron h=6.626×10-34J·s,p, Planck’s constant λ= = h mc h p E = mc2 = h