(4)用A表示KVL的矩阵形式 ② 以b(=6)阶列向量表示支路电压: 3 ① ③ u=[41,··,46]T 并取某一结点(取④)为参考, 2 5 (n-1=3)个结点电压的列向量: ④ un=[um:un2,un3 ]T 结点电压与支路电压之间的关系为 u=ATun uj -unt+un3 -1 0 1 u -Unl 1 可以认为, 0 0 1-1 W 这是用A表示 Unt-Un2 3 0 Us 一1Wn2 Un3 0-1 1 Un2 KVL的矩阵 Un3 00 1 un3 形式。 6 Un2 0 1 0_ AT 11
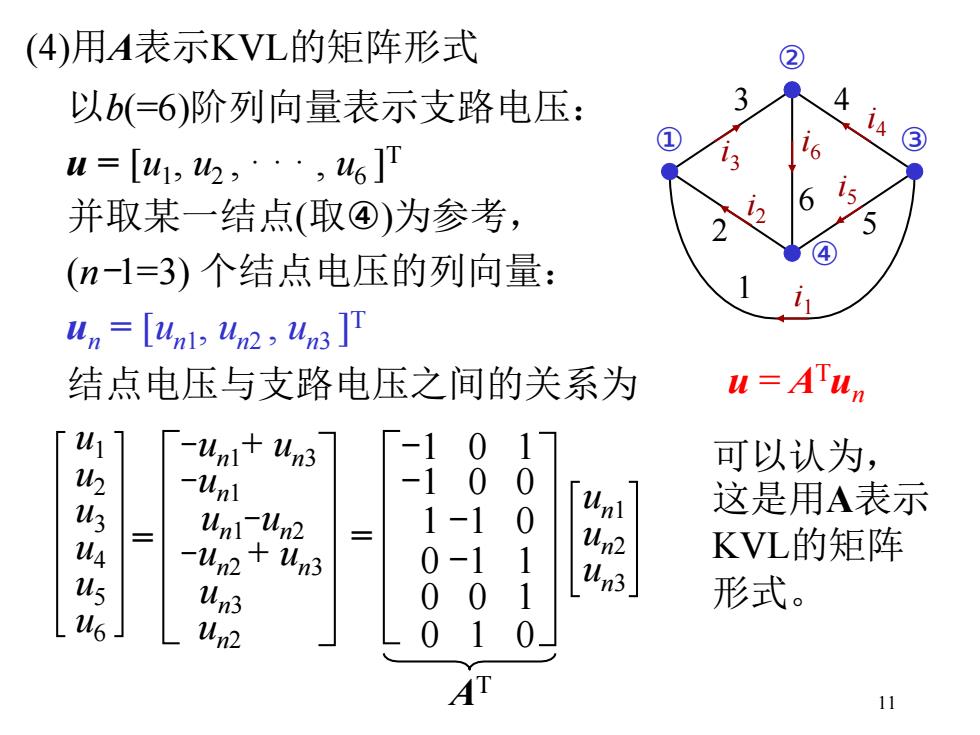
(4)用A表示KVL的矩阵形式 以b(=6)阶列向量表示支路电压: u = [u1 , u2 , · · · , u6 ] T 并取某一结点(取④)为参考, (n-1=3) 个结点电压的列向量: un = [un1 , un2 , un3 ] T 结点电压与支路电压之间的关系为 u = ATun u1 u2 u3 u4 u5 u6 = 1 i 1 2 i 2 3 i 3 4 i 4 5 i 5 i 6 6 ① ② ③ ④ -un1+ un3 -un1 un1 -un2 -un2 + un3 un3 un2 = un1 un2 un3 -1 0 1 -1 0 0 1 -1 0 0 -1 1 0 0 1 0 1 0 AT 可以认为, 这是用A表示 KVL的矩阵 形式。 11

小结 ①矩阵A表示有向图结点与支路的关联性质。 ②用A表示的KCL的矩阵形式为Ai=0 ③用A表示的KVL的矩阵形式为W=ATun 12
小结 ① 矩阵 A表示有向图结点与支路的关联性质。 ③ 用 A表示的 KVL 的矩阵形式为 u = ATun ② 用 A表示的 KCL 的矩阵形式为 Ai =0 12
2.回路矩阵 描述回路与支路关联的矩阵。 是一个(Ixb)阶的矩阵。 (1)B的元素定义 b+1,支路k与回路关联,且方向一致; b二-1,支路k与回路关联,且方向相反; b0,支路k与回路无关联。 ② 3 123456 1 1 0 1 1 B=2 011 0 0 1 30001-1 1 13
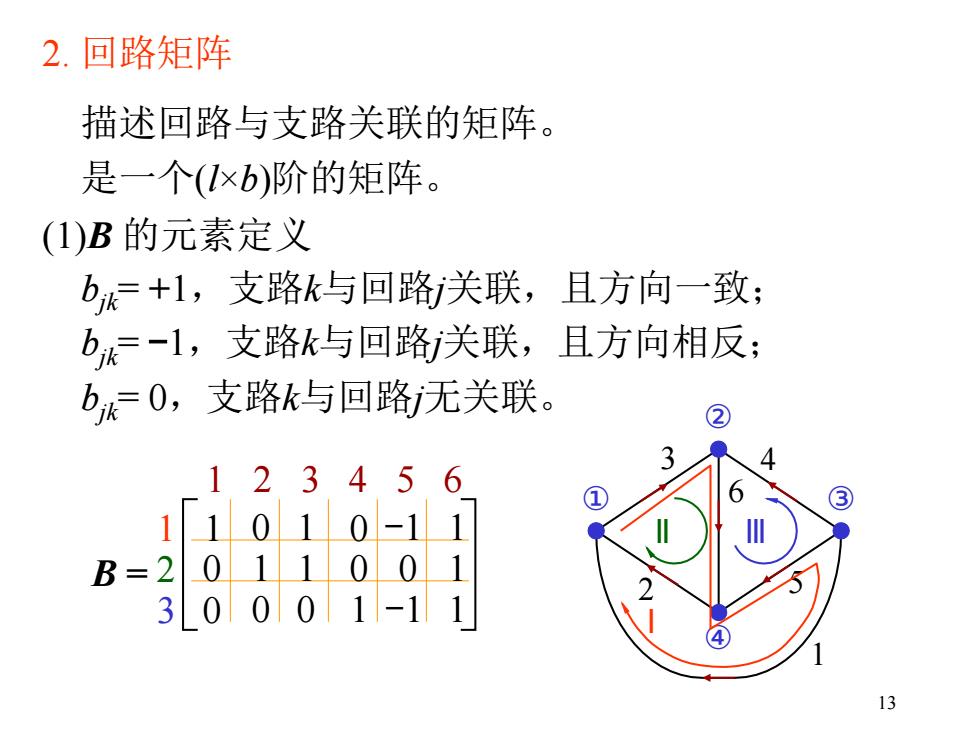
2. 回路矩阵 描述回路与支路关联的矩阵。 是一个(l×b)阶的矩阵。 (1)B 的元素定义 bjk= +1,支路k与回路j关联,且方向一致; bjk= -1,支路k与回路j关联,且方向相反; bjk= 0,支路k与回路j无关联。 1 2 3 1 2 3 4 5 6 1 1 2 3 4 5 ① 6 ② ③ ④ Ⅰ 0 1 0 -1 1 Ⅱ Ⅲ 0 1 1 0 0 1 0 0 0 1 -1 1 B = 13
(2)基本回路矩阵B, ② B反映了一组单连支回路与 支路间的关联关系。 写B时的排列顺序: 先连支后树支。 B,=111 B,] 1243 56 1 0 01-1 B =2010 101 300 0-11 Bu=0 (3)用B表示的KVL矩阵形式 41 :u1+w3-45+l6=0 1010 -1 1 u; 0 l:w2+u3+6=0 0 0 us 0 Il:445+u。=0 .0001 -1 us 0 6 14
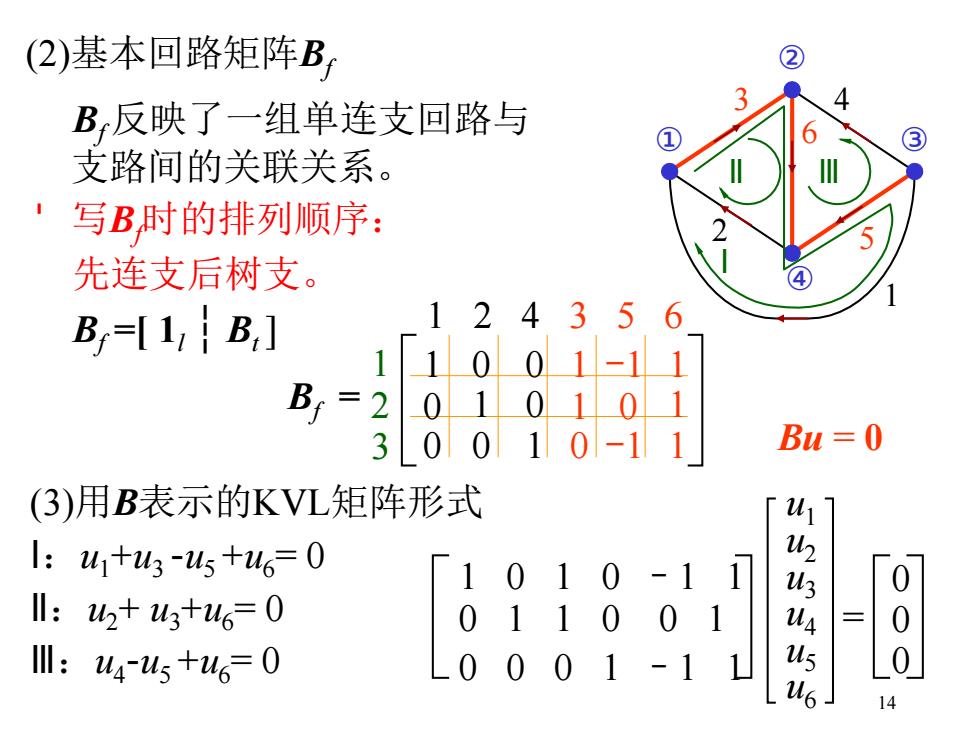
(2)基本回路矩阵Bf Bf 反映了一组单连支回路与 支路间的关联关系。 ' 写Bf时的排列顺序: 先连支后树支。 Bf =[ 1l ┆ Bt ] (3)用B表示的KVL矩阵形式 Ⅰ:u1+u3 -u5 +u6= 0 Ⅱ:u2+ u3+u6= 0 Ⅲ:u4 -u5 +u6= 0 1 2 3 4 5 ① 6 ② ③ ④ Ⅰ Ⅱ Ⅲ 1 2 3 1 2 4 3 5 6 1 0 0 1 -1 1 0 1 0 1 0 1 0 0 1 0 -1 1 Bf = Bu = 0 1 0 1 0 –1 1 0 1 1 0 0 1 0 0 0 1 –1 1 u1 u2 u3 u4 u5 u6 = 0 0 0 14

(4)用B表示的KCL矩阵形式 ② 若用列向量表示(=3)个独立回 路电流: i=[iin·. inJ 则支路电流与回路电流之间的 4 关系可以表示为 i=BTi 007 0 1 0 可以认为是用 1 1 0 4 in+in B表示KCL的 0 0 1 g -1 0-1 矩阵形式。 1 1 -in-iB 1 in+in+in 15
(4)用B表示的KCL矩阵形式 若用列向量表示 l(=3) 个独立回 路电流: i l = [i l1 il2 · · · i ll] T 则支路电流与回路电流之间的 关系可以表示为 i = BT i l 可以认为是用 B 表示KCL的 矩阵形式。 1 2 3 4 5 ① 6 ② ③ ④ Ⅰ Ⅱ Ⅲ i 1 i 2 i 3 i 4 i 5 i 6 = i l1 i l2 i l3 1 0 0 0 1 0 1 1 0 0 0 1 -1 0 -1 1 1 1 i i1 i l2 i l1+i l2 i l3 -i l1 -i l3 i l1+i l2 +i l3 = 15