
第八章相量法 内容提要 1.正弦量及其三要素、相位差的概念; 2.相量法的概念及其性质; 3.电路定律和元件VCR的相量形式。 Im=5∠45oA 450 Z= Um =20∠-4502 Um100∠0°V 2025年4月2日星期三
2025年4月2日星期三 1 第八章 相量法 内容提要 1.正弦量及其三要素、相位差的概念; 2.相量法的概念及其性质; 3.电路定律和元件VCR的相量形式。 . Im= 5∠45o A . Um= 100∠0 o V 45o Z = . Um . Im =20∠-45o W

重点 1.正弦量和相量之间的关系; 2.正弦量的相量差和有效值的概念; 3.R、L、C各元件的电压、电流关系的相量形式; 4.电路定律的相量形式及元件的电压电流关系的 相量形式。 难点 1.正弦量与相量之间的联系和区别; 2.元件电压相量和电流相量的关系。主要是相位关系 是学习第9~12章的基础,必须 熟练掌握相量法的解析运算。 2025年4月2日星期三 2
2025年4月2日星期三 2 重点 难点 1. 正弦量与相量之间的联系和区别; 2. 元件电压相量和电流相量的关系。 1.正弦量和相量之间的关系; 2.正弦量的相量差和有效值的概念; 3. R、L、C各元件的电压、电流关系的相量形式; 4.电路定律的相量形式及元件的电压电流关系的 相量形式。 主要是相位关系 是学习第 9~12 章的基础,必须 熟练掌握相量法的解析运算

§8-1复数 1.复数的表示形式 3)指数和极坐标形式 (1)代数形式F=a+jb 根据欧拉公式 Re[F]=a,Im[F]=6 eio=cos0 +isin0 (2)三角形式 得指数形式: F=F(cos0+jsinθ) F=Feio a=Fcos0,b=Flsine 或写成极坐标形式: 1F1=√a2+b2 F=FO 0= arctg b 2025年4月2日星期三
2025年4月2日星期三 3 §8-1 复数 1. 复数的表示形式 (1)代数形式 F=a+jb Re[F]=a, Im[F]=b (2) 三角形式 F=| F |(cosq + jsinq ) a=| F |cosq,b=| F |sinq (3)指数和极坐标形式 根据欧拉公式 e jq =cosq +jsinq 得指数形式: F = | F | e jq 或写成极坐标形式: | F | = a 2 + b 2 F = | F | q q = arctg b a
(4)矢量形式 复数加、减的图解 +] F=F+F2 a +1 +1 b 2.复数的运算 F=F-F2 ()加减 用代数形式最好 设F1=1+jb1F2=2+jb2 则F1±F2=(a1±2)+j(b1±b2) 2025年4月2日星期三
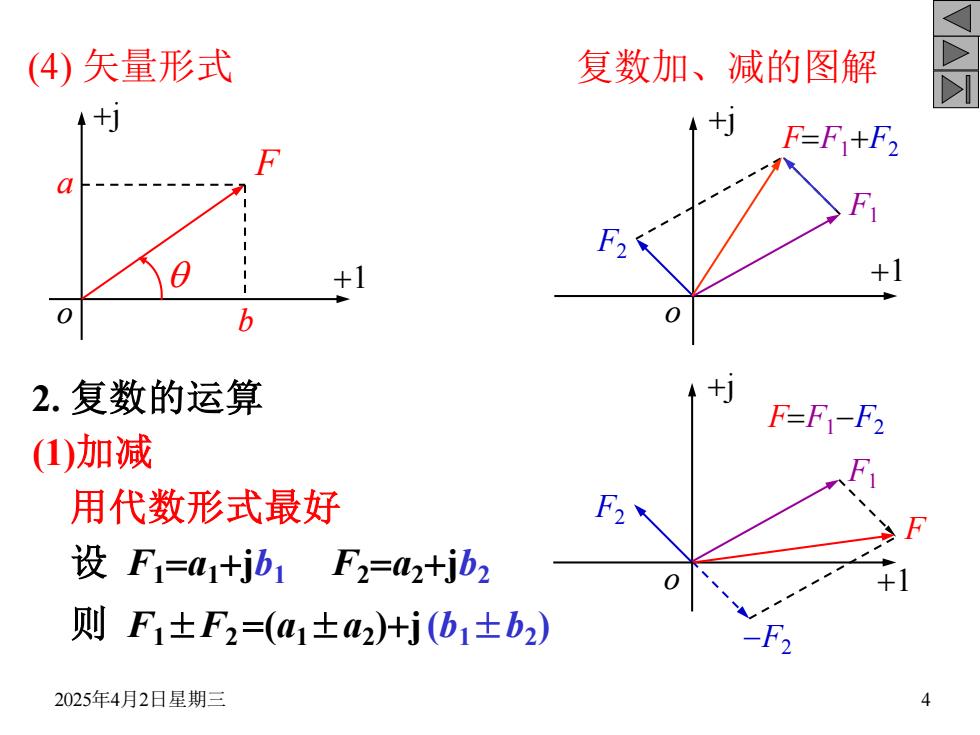
2025年4月2日星期三 4 (4) 矢量形式 2. 复数的运算 (1)加减 用代数形式最好 设 F1=a1+jb1 F2=a2+jb2 则 F1±F2 =(a1±a2 )+j(b1±b2 ) 复数加、减的图解 o +j +1 F a b q +j o +1 F1 F2 F=F1+F2 F=F1-F2 -F2 +j o +1 F1 F2 F

(2)乘除 用指数或极坐标形式最好 F=Fei01,F2=F2 ei2 F-FF2=FF2lei(0+2) 或F=FIIF2I/8+8 F= 1 F F2 /8-6 -F2 乘(除)法运算满足模相乘(除),辐角相加(减)。 8若两个复数相等F1=F 则必须是Fl=|F2,O=8 或是a1=2,jb=jb2 2025年4月2日星期三 5
2025年4月2日星期三 5 (2) 乘除 用指数或极坐标形式最好 设 F1= |F1 | e jq 1, F2 = |F2 | e jq 2 则 F=F1 F2 = |F1 | |F2 | e j(q1+q 2) F = |F1 | |F2 或 | q1+q2 F = q1-q2 F1 F2 = |F1 | |F2 | 若两个复数相等 F1 = F2 则必须是 |F1 | = |F2 |,q1=q2 或是 a1 = a2, jb1= jb2 乘(除)法运算满足模相乘(除),辐角相加(减)