3.割集矩阵9 描述割集与支路关联的矩阵。 Q是一个(n-1)×b阶的矩阵。各元素定义为: 9+1,支路k与割集关联,且方向一致: 4-1,支路k与割集关联,且方向相反: Ak=0,支路k与割集无关联。 ③ 123456 1-1-11 0 0=2100 0 3-1-1 0-1 若选单树支割集为一组独立割集, 则得到基本割集矩阵 排列顺序为先树支后连支。 2[12] 6
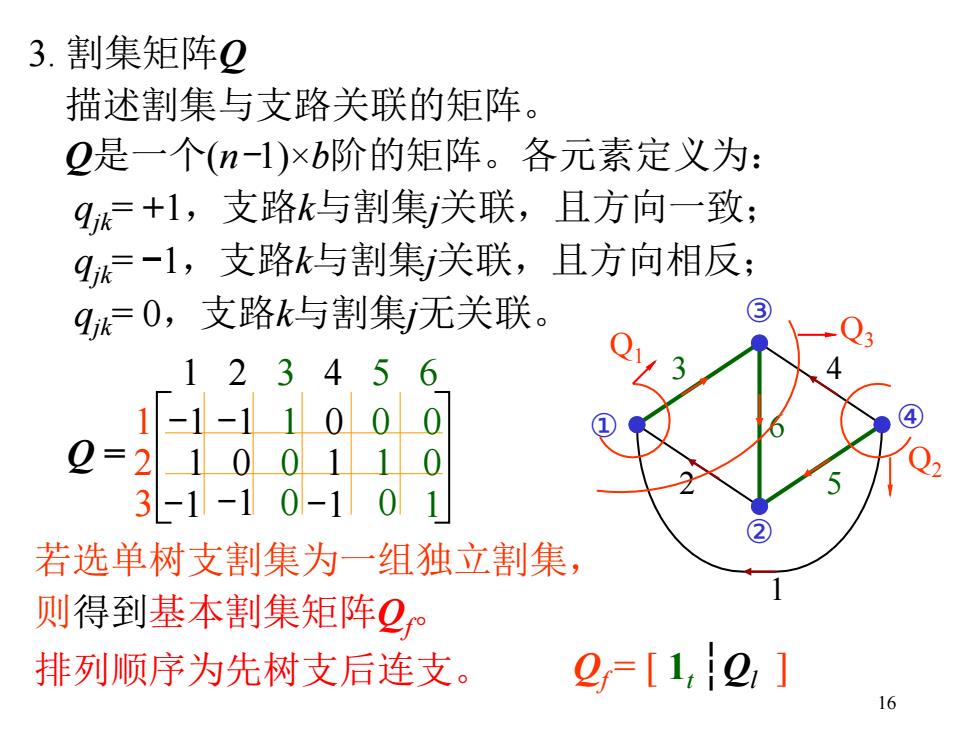
3. 割集矩阵Q 描述割集与支路关联的矩阵。 Q是一个(n-1)×b阶的矩阵。各元素定义为: qjk= +1,支路k与割集j关联,且方向一致; qjk= -1,支路k与割集j关联,且方向相反; qjk= 0,支路k与割集j无关联。 若选单树支割集为一组独立割集, 则得到基本割集矩阵Qf。 排列顺序为先树支后连支。 1 2 3 4 5 ① 6 ② ③ 1 ④ 2 3 1 2 3 4 5 6 Q1 -1 -1 1 0 0 0 1 0 0 1 1 0 -1 -1 0 -1 0 1 Q2 Q3 Qf = [ 1t ┆Ql ] Q = 16
35612 4 100-1-1 07 0-[1,2]= 010 0 1 2 001-1-1-1Q3 ③ (1)用割集矩阵Q表示的 KCL的矩阵形式 因属同一割集的所有支路 的电流也满足KCL,所以 2i=0 -1-11 0 0 0 -i1-i2+i3 0 23 10 11 0 i1+i4+i5 -1-10-10 1 +0 61 1
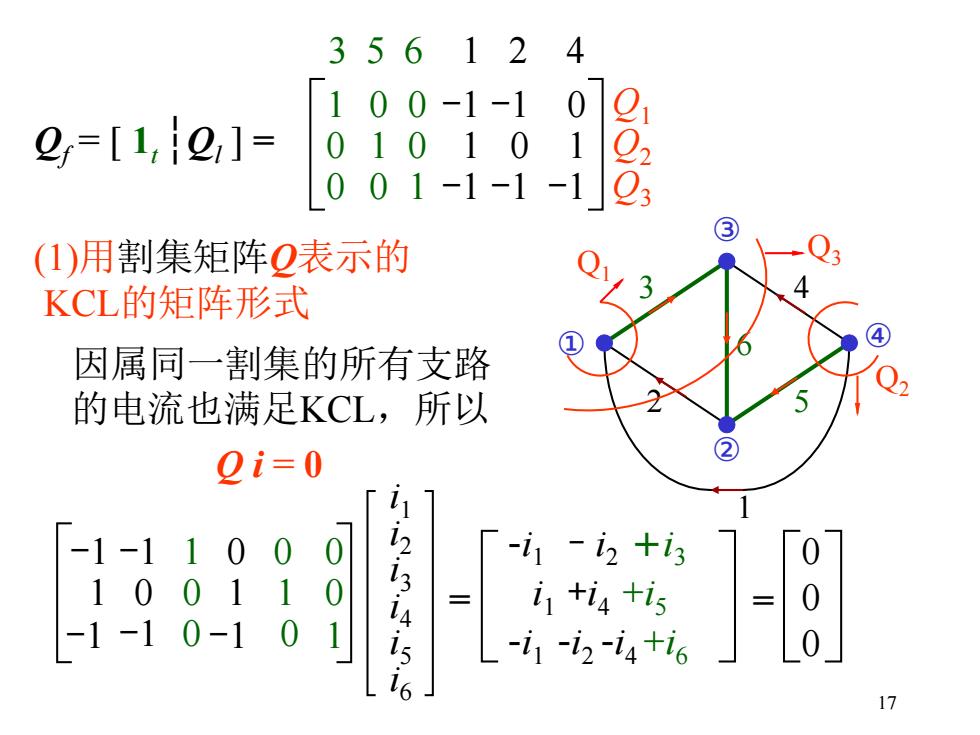
(1)用割集矩阵Q表示的 KCL的矩阵形式 因属同一割集的所有支路 的电流也满足KCL,所以 Q i = 0 1 2 3 4 5 ① 6 ② ③ ④ Q1 Q2 Q3 -1 -1 1 0 0 0 1 0 0 1 1 0 -1 -1 0 -1 0 1 i 1 i 2 i 3 i 4 i 5 i 6 = -i 1 –i 2 +i 3 i 1 +i 4 +i 5 -i 1 -i 2 -i 4 +i 6 = 0 0 0 Qf = [ 1t ┆Ql ] = 1 0 0 0 1 0 0 0 1 -1 1 -1 -1 0 -1 0 1 -1 3 5 6 1 2 4 Q1 Q2 Q3 17