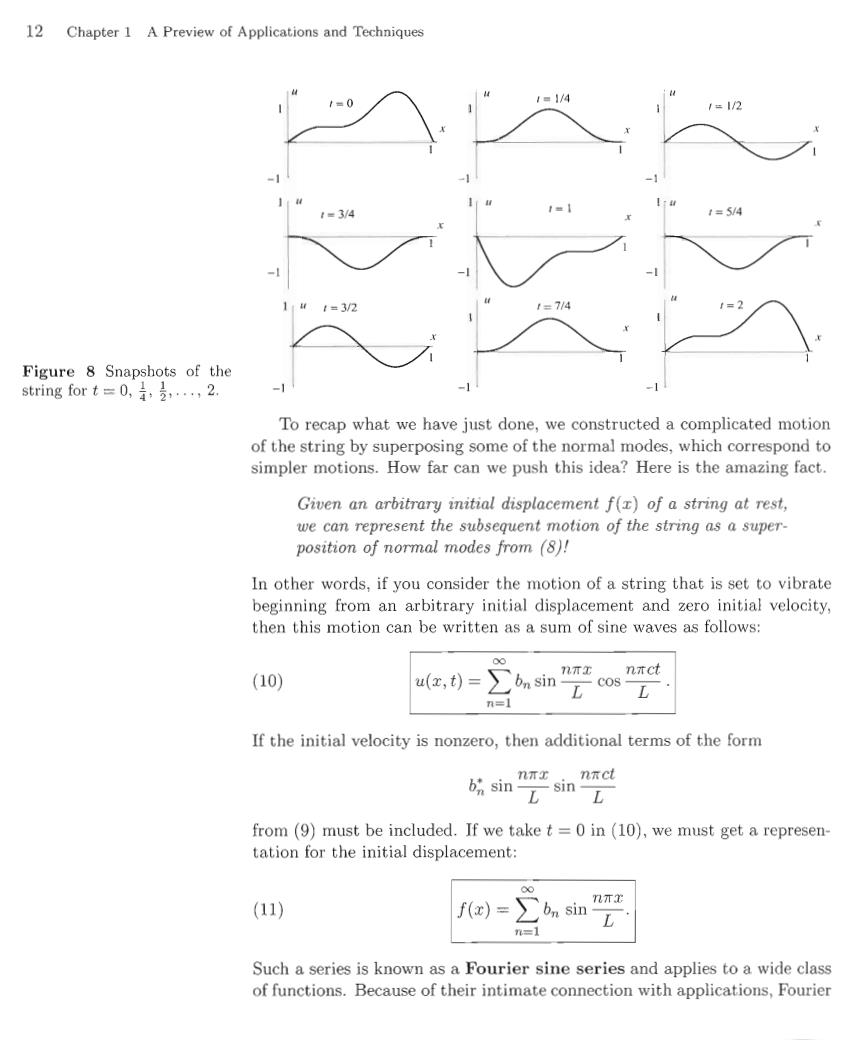
12 Chapter 1 A Preview of Applications and Techniques t=0 1=1/4 1=1/2 t=3/4 1=5/4 t=3/2 1=714 2 Figure 8 Snapshots of the string for t=2. To recap what we have just done,we constructed a complicated motion of the string by superposing some of the normal modes,which correspond to simpler motions.How far can we push this idea?Here is the amazing fact. Given an arbitrary initial displacement f(r)of a string at rest, we can represent the subsequent motion of the string as a super- position of normal modes from (8)! In other words,if you consider the motion of a string that is set to vibrate beginning from an arbitrary initial displacement and zero initial velocity, then this motion can be written as a sum of sine waves as follows: 00 (10) T u(,t)=∑onsin” nct COS- L n=1 If the initial velocity is nonzero,then additional terms of the form nTT nict bsin元sin from(9)must be included.If we take t =0 in (10),we must get a represen- tation for the initial displacement: 0 (11) f)=∑ nnE n=1 Such a series is known as a Fourier sine series and applies to a wide class of functions.Because of their intimate connection with applications,Fourier

Section 1.2 Solving and Interpreting a Partial Differential Equation 13 sine series,and,more generally,Fourier series will be studied in great detail in Chapter 2.In particular,we will derive formulas for the coefficients on in the Fourier sine series (11). The fact that the general motion of the vibrating string can be expressed as an infinite sum of sine waves,as in (10),was first claimed by the Swiss mathematician Daniel Bernoulli (1700-1782)around 1750.Thus Bernoulli was the first one to introduce Fourier series to the solution of partial differ- ential equations.(Of course,the expression Fourier series was not known at that time.)Soon after it was announced,Bernoulli's claim was dismissed by another Swiss mathematician,the great Leonhard Euler(1707-1783),on the ground that,if it were true,it would imply that every function can be expressed as an infinite sum of sine functions,as we just saw in (11).Euler doubted the validity of these (Fourier)sine series expansions and rejected Bernoulli's approach altogether.Euler's doubts were dispelled decades later, with the ingenious work of the French mathematician Joseph Fourier (1768- 1830).Fourier's work was also met with doubts and was rejected when it was first presented to the French Academy,in 1807.In 1811,Fourier resub- mitted his theory to the Academy who then recognized its importance and awarded him its grand prize. Preview of Applications and Methods We have seen how the modeling of the vibrating string led to a partial differential equation,the one dimensional wave equation.The vibrating string is only our starting point in the applications.In this book we will meet other problems dealing with vibrations of strings,membranes,plates, and rods,oscillations of chains,heat transfer in various media,and many more.As you have just seen,the solution of the vibrating string involved expanding functions in Fourier sine series.The solutions of many of the foregoing problems lead naturally to expansions in specific functions,other than sine functions,which are tailored to the problem at hand.For example, you will encounter Bessel functions and Bessel series expansions,Legendre polynomials and Legendre series expansions,and other special functions and their associated series expansions. To give a more complete picture of the techniques involved in this book, we mention the method of separation of variables.Roughly speaking,this method allows you to reduce solving a given partial differential equation to solving several ordinary differential equations.The solutions of these ordinary differential equations determine the kind of expansion that is ap- propriate to a given problem.The method of separation of variables will be introduced in Chapter 3 and used in almost all of the subsequent chapters

14 Chapter 1 A Preview of Applications and Techniques Exercises 1.2 1.Suppose that u=u(x,t)and v=v(,t)have partial derivatives related in the following way: 8v Ou and Ot 。 Show that u and v are solutions of the wave equation (1)with c =1. 2.Consider the equations in Exercise 1 supplemented by the initial data u(x,0)=f(x),v(x,0)=h(r) (a)Show that the appropriate initial data for the wave equation for u is u(红,0)=fx), 费,0=-t (b)Find the appropriate initial data for the wave equation for v. 3.Let.F and G be arbitrary differentiable functions of one variable.Show that u(r,t)=F(x+ct)+G(z-ct)is a solution to the wave equation (1),provided that F and G are sufficiently smooth.(This solution will be derived in the next exercise.) 4.(a)Use the change of variables a =x+ct,B=x-ct to transform the wave equntion()into品a=0.(Youshoud assume that2品=22a,) (b)Integrate the equation with respect to a to obtaing(B),where g is an arbitrary function. (c)Integrate with respect to B to arrive at u F(a)+G(B),where F is an arbitrary function and G is an antiderivative of g. (d)Derive the solution given in Exercise 3. 5.(a)Using the solution in Exercise 3,solve the wave equation with initial data uz,0)=1+2 1 (,0)=0,-∞<x<0. (b)Take c =1,and plot the solution for-15<<15 and t=0,1,2,4.6,8. Observe that half the wave moves to the left and the other half moves to the right. 6.Repeat Exercise 5(a)for the data u(,0)=e,()0,<<. 7.Repeat Exercise 5(a)with u(,0)=0,(0)=-2xe<<. 8.Repeat Exercise 5(a)for the data u(,0)=0,(0)=o<<. 9.Solve the wave equation with initial data 1 u(x,0)=1+x2 (红,0)=-2xe,-00<x<o. Hint:Use Exercises 5 and 7 and superposition.] 10.Use Exercises 6 and 8 and superposition to solve the wave equation with initial data Mz.0)=e, 元,0)=1+r2P -00<x<00

Section 1.2 Solving and Interpreting a Partial Differential Equation 15 11.Consider an electrical cable running along the z-axis that is not well insulated from ground,so that leakage occurs along its entire length.Let V(z,t)and I(c,t) denote the voltage and current at point x in the wire at time t.These functions are related to each other by the system Ox RI and =-COv -GV Ox where L is the inductance,R is the resistance,C is the capacitance,and G is the leakage to ground.Show that V and I each satisfy 0r2 =LC Ou 82u Ou +(RC+LG)+RGu, which is called the telegraph equation. 12.In the second frame in Figure 5(for t =1/4),the maximum of the displacement appears to be larger than 1/2.Explain this,and if possible compute the value of the maximum. 13.Referring to Figure 8,explain why frames 2,4,6,and 8 appear to be symmetric about x 1/2. 14.Referring to Figure 8,explain why the displacements in frames 2,4,6,and 8 appear to obey the end conditions u(0,t)=0=u(1,t)and 产a.0-8 1,)=0 In Erercises 15-20,you are asked to solve the wave equation (1)subject to the boundary conditions (3),(4).and the initial conditions (5),(6),for the given data. Hint:Use (10)and the remark that follows it. 15.f(x)=sin2平,gx)=0. 16.fx)=支sin譬+寺sin3',g(z)=0. 17.fx)=支sin号+}sin2+弟sin',g(x)=0. 18.f(x)=0,9x)=sin号. 19.f(z)=0,g(x)=}sin3平-六sin吧 20.fx)=sin2平cos2¥,g(x)=0. 21.(a)Taking c=L=1,plot several snapshots of the vibrating string in Exer- cise 15.Observe that the point at x=never moves.Prove this last observation. (b)Find initial data for which the point x=never moves.Show that the point x=号is also fixed.. 22.(a)Solve the wave equation with c =1,boundary conditions (3),(4)with L 1,and initial data f()=sin 2x+sin4nx,g()=0. (b)Plot several snapshots of the string.How many fixed points do you see in the interval 0<<1?Justify your answer. 23.In this exercise,we consider how a given point on a vibrating string moves with time.Consider the solution of Exercise 15 with c =L=1.Fix x =xo and plot u(ro,t)as a function oft,for0<t<20,for zo=,寺,,是.Observe that in each case we get a cosine wave and that all the curves are identical except for a scaling factor

16 Chapter 1 A Preview of Applications and Techniques 24.Repeat Exercise 23 for the data given in Exercise 22.What do you observe? 25.Show that the solution(2)has initial data at time togiven by u(x,to)=0 and du C πE (z,to)=sin L' 26.Let u(,t)be the solution given by (2).Show u(,)is the solution given by (7).What does this imply about the motion described by (2)versus the one described by (7)? 27.The advection equation.This is the equation (12) Ou .0u ,)=-大a红,)+kx,t, where k is a positive constant and k is a function of (a,t).It is used in model- ing AIDS epidemics,fluid dynamics,and other situations involving matter that is carried along with a fow of air or water.As a concrete application,suppose that the wind is blowing in one direction at the speed of K meters per second,say,the positive direction on the z-axis,and it is carrying with it a certain pollutant from a factory located at the origin.Let u(x,t)denote the density (number of parti- cles per meter)at time t,and suppose that the particles are falling out of the air at a constant rate proportional to u(x,t),with constant of proportionality r>0. Then u satisfies (12)with k(z,t)=-ru(x,t).(For a derivation and references see Modeling Differential Equations in Biology,by Clifford Henry Taub,Prentice Hall, 2001.) Figure 9 The number of par- ▣口 ticles at time t between x and r+△xisu(x,t)△x. x+△x (a)Show that all the solutions of Ou (2,t0=- -9 are of the form u(z,t)=ertf(x-kt).[Hint:Use a change of variables as we did in Example 3,Section 1.1.] (b)Let Al denote the number of particles in the air at time t =0.Show that the number of particles at time t >0 is eM.Hint:The number of particles is the integral of the density function over the interval -oo <x<oo