
Topics to Review This chapter is independent of 2 the previous one.The core ma- terial (Sections 2.1-2.4)requires only a basic knowledge of calcu- FOURIER SERIES lus.An elementary knowledge of complex numbers is required for Section 2.6.Sections 2.5,2.8.2.9. Mathematics compares the most diverse phenomena and discovers the and 2.10 are self-contained ad- secret analogies that unite them. vanced topics.The applications -JOSEPH FOURIER in Section 2.7 involve ordinary differential equations with con- stant coefficients. Background for this section is found in Ap- pendix A.2. Looking Ahead... Fourier series,as presented in Like the familiar Taylor series,Fourier series are special types Sections 2.1-2.4.are essential for all that follows and cannot be of expansions of functions. With Taylor series,we are inter- omitted. ested in expanding a function in terms of the special set of func- Sections 2.5 and 2.8-2.10 contain tions 1,a,x2,x3,.... With Fourier series,we are interested theoretical properties of Fourier in expanding a function in terms of the special set of functions serics. They may be omitted 1,cosx,cos2x,cos3x,...,sinz,sin2x,sin3x,....Thus,a Fourier without affecting the continuity series expansion of a function f is an expression of the form of the book. However.they are strongly recommnended in a 00 course emphasizing Fourier se- f(x)=a0+ an cos nx +bn sin nx). ries.In particular,the proof of n= the Fourier series representation theorem in Scction 2.8 reveals in- Fourier series arose naturally when we discussed the vibrations of a teresting ideas from Fourier anal- plucked string(Section 1.2).As we will see in the following chapters, ysis. Fourier series are indeed the most suitable expansions for solving cer- Seetion 2.6 serves as a good mo- tain classical problems in applied mathematics.They are fundamental tivation for the Fourier transform to the description of important physical phenomena from diverse fields, in Chapter 7. such as mechanical and acoustic vibrations,heat transfer,planetary In Section 2.7 we study the forced motion,optics,and signal processing,to name just a few. oscillations of mechanical or elec- trical systems.While the cqua- The importance of Fourier series stems from the work of the French tions that arise are ordinary dif- mathematician Joseph Fourier,who claimed that any function defined ferential equations,their solu- on a finite interval has a Fourier series expansion.The purpose of this tions require topics such as lin- chapter is to investigate the validity of Fourier's claim and derive the earity of equations and superpo- basic properties of Fourier series,preparing the way for the important sition of solutions that are very applications of the following chapters. useful in later chapters

18 Chapter 2 Fourier Series 2.1 Periodic Functions As we saw in Section 1.2,Fourier series are essential in solving certain partial differential equations.In this section we introduce some basic concepts that will be useful for our treatment of the general theory of Fourier series. Consider the function sinx whose graph is shown in Figure 1.Since the values of sinx repeat every 2m units,its graph is obtained by repeating the portion over any interval of length 2m.This periodicity is expressed by the 2π identity sinx sin(x+2m)for all 2π In general,a function f satisfying the identity 2 0 2π (1) f(x)=f(x+T)for all x, where T >0,is called periodic,or more specifically,T-periodic(Figure 2). The number T is called a period of f.If f is nonconstant,we define the Figure 1 Graph of sinz. fundamental period,or simply,the period of f to be the smallest positive number T for which(1)holds.For example,the functions 3,sinx,sin 2x are all 2m-periodic.The period of sinx is 2m,while the period of sin 2x is m. Using(1)repeatedly,we get f(z)=f(x+T)=f(x+2T)=...=f(x+nT) Hence if T is a period,then nT'is also a period for any integer n >0.In the case of the sine function,this amounts to saying that 2,4,6m,...are all periods of sina,but only 2 is the fundamental period.Because the Figure 2 A T-periodic func- values of a T-periodic function repeat every T units,its graph is obtained tion. by repeating the portion over any interval of length T (Figure 2).As a consequence,to define a T-periodic function,it is enough to describe it over an interval of length T.Obviously,the interval can be chosen in many different ways.The following example illustrates these ideas. 一x+ EXAMPLE 1 Describing a periodic function Describe the 2-periodic function f in Figure 3 in two different ways: (a)by considering its values on the interval 0<z<2; (b)by considering its values on the interval-1 <x<1. Solution (a)On the interval 0<x<2 the graph is a portion of the straight line y=-2+1.Thus f(x)=-x+1if0≤x<2. Figure 3 A 2-periodic func- tion. Now the relation f(x+2)=f(x)describes f for all other values of

Section 2.1 Periodic Functions 19 (b)On the interval-1 <<1,the graph consists of two straight lines (Figure 3). We have -x-1if-1≤x<0, f)={-E+1if0≤x<1. As in part (a),the relation f(x+2)=f(x)describes f for all values of x outside the interval [-1,1). ■ Although the formulas in Example 1(a)and (b)are different,they de- scribe the same periodic function.We use common sense in choosing the most convenient formula in a given situation(see Example 2 of this section for an illustration). Piecewise Continuous and Piecewise Smooth Functions We now present a class of functions that is of great interest to us.The important terminology that we introduce will be used throughout the text. Consider the function f(c)in Figure 3.This function is not continuous at x=0,±2,±4,..Take a point of discontinuity,sayx=0.The limit of the function from the left is-1,while the limit from the right is 1.Symbolically, this is denoted by f(0-)=lim f(x)=-1 and f(0+)=lim f(x)=1. x0- x→0+ f(c-) In general,we write f(c-)=lim f(x) 工+C” f(c+) to denote the fact that f approaches the number f(c-)as x approaches c from below.Similarly,if the limit of f exists as approaches c from above, we denote this limit f(c+)and write f(c+)=limf(x) Figure 4 Left and right lim- x+C十 its. (Figure 4).Recall that a function f is continuous at c if f(c)=lim f(x). CwC In particular,f is continuous at c if and only if f(c-)=f(c+)=f(c). A function f is said to be piecewise continuous on the interval [a,b if PIECEWISE f(a+)and f(b-)exist,and CONTINUOUS f is defined and continuous on (a,b)except at a finite number of points FUNCTIONS in (a.b)where the left and right limits exist. A periodic function is said to be piecewise continuous if it is piecewise continuous on every interval of the form [a,b.A periodic function is said

20 Chapter 2 Fourier Series to be continuous if it is continuous on the entire real line.Note that (0+ continuity forces a certain behavior of the periodic function at the endpoints of any interval of length one period.For example,if f is T-periodic and continuous,then necessarily f(0+)=f(T'-)(Figure 5). The function in Example 1 enjoys another interesting property in addi- tion to being piecewise continuous.Because the slopes of the line segments on the graph of f are all equal to-1,we conclude that f'(z)=-1 for all x≠0,±2,±4,.So the derivative f'(x)exists and is continuous for all x≠O,±2,±4,,,and at these exceptional points where the derivative does Figure 5 A continuous T- not exist,the left and right limits of f'(x)exist (indeed,they are equal to periodic function. -1).In other words,f'(r)is piecewise continuous.With this example in mind,we introduce a property that will be used very frequently. A function f,defined on the interval [a,b],is said to be piecewise smooth if PIECEWISE f and f are piecewise continuous on [a,b.Thus f is piecewise smooth if SMOOTH FUNCTIONS f is piecewise continuous on [a,bl, f exists and is continuous in (a,b)except possibly at finitely many points c where the one-sided limits lim f(r)and lim f(r)exist.Furthermore,lim f'()and lim f(r)exist. A periodic function is piecewise smooth if it is piecewise smooth on every interval [a,b].A function f is smooth if f and f'are continuous. The function sinz is smooth.The function in Example 1 is piecewise smooth but not smooth.The function z1/3 for-1 <z<1 is not piecewise smooth because neither the derivative nor its left or right limits exist at =0.Additional examples are discussed in the exercises. The following useful theorem,whose content is intuitively clear,states that the definite integral of a T-periodic function is the same over any interval of length T (Figure 6). THEOREM 1 Suppose that f is piecewise continuous and T-periodic.Then,for any real INTEGRAL OVER number a,we have ONE PERIOD f()dz Proof To simplify the proof,we suppose that f is continuous.For the general case,see Exercise 26.Define a+7 F(a)= f()dx
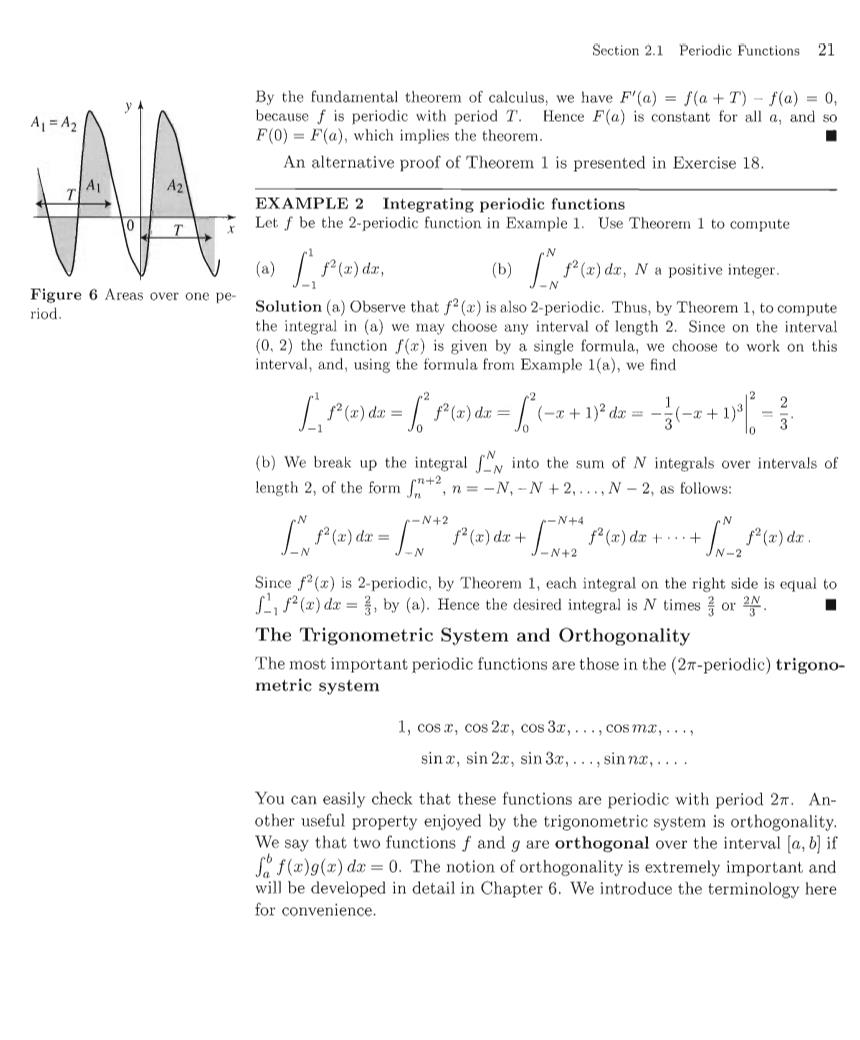
Section 2.1 Periodic Functions 21 By the fundamental theorem of calculus,we have F(a)=f(a+T)-f(a)=0, A=A because f is periodic with period T.Hence F(a)is constant for all a,and so F(0)=F(a),which implies the theorem An alternative proof of Theorem 1 is presented in Exercise 18. EXAMPLE 2 Integrating periodic functions Let f be the 2-periodic function in Example 1.Use Theorem 1 to compute (a) f2()dr, (b) f2(z)dr,N a positive integer. -N Figure 6 Areas over one pe- riod. Solution (a)Observe that f2(a)is also 2-periodic.Thus,by Theorem 1,to compute the integral in (a)we may choose any interval of length 2.Since on the interval (0.2)the function f()is given by a single formula,we choose to work on this interval,and,using the formula from Example 1(a),we find reo=re=-e+=-e+y川 2 (b)We break up the integral into the sum of N integrals over intervals of length 2,of the form n =-N,-N +2....,N-2,as follows: W+2 -N+4 N f2(x)dr+…+ f2(x)dr. =N+2 IN-2 Since f2(x)is 2-periodic,by Theorem 1,each integral on the right side is equal to ()d=by (a).Hence the desired integral is N timesor ■ The Trigonometric System and Orthogonality The most important periodic functions are those in the(2r-periodic)trigono- metric system 1,C0sE,C0s2t,C0s3x,·,C0smx,·, sinx,sin2x,sin3x,.,sinna,·· You can easily check that these functions are periodic with period 2.An- other useful property enjoyed by the trigonometric system is orthogonality. We say that two functions f and g are orthogonal over the interval [a,b]if f((d=0.The notion of orthogonality is extremely important and will be developed in detail in Chapter 6.We introduce the terminology here for convenience