上海交通大学：《随机模拟方法与应用 Stochastic Simulation Methods and Its Applications》课程教学资源（学生作业）对MCMC 方法在瑞利分布样本采集及一元线性回归模型参数估计中应用的思考与研究——吴凯斌

《随机模拟方法与应用》课程大作业 2015年度春季学期 对MCMC方法在瑞利分布样本采集及一元线性回归模型参 数估计中应用的思考与研究 学号：5110109140 姓名：吴凯斌 授课老师：肖柳青 1.全文内容概要 本文基于统计学中有关瑞利分布及一元线性回归分析的参考文献，主要对马尔可夫链蒙 特卡罗方法（即MCMC方法）在瑞利分布样本采集以及一元线性回归模型参数估计中的应 用进行了思考与研究。全文共分为三大部分：首先，简单介绍了马尔科夫链的数学概念，并 通过提出一个具体的模型来说明其表示方法：其次，介绍了MCMC方法在电子工程中常用 的一个数学分布一一瑞利分布中随机采集若干个样本的具体应用，并将算法通过matlab加 以实现：最后，介绍了MCMC算法在一元线性回归模型参数估计中的应用思想，并将其与 最小二乘法进行了对比。 2.马尔可夫链的概念及其表示方式 无论是世界上重大的政治局势变化，还是我们每个人生活中的一些非常琐碎的事情，它 们之间绝大多数都是有着一定的因果关系的，也就是说每件事情的发生都会对接下来出现的 事情产生一定的影响，这种影响可以是有形的，也可以是无形的，其最终将反映到接下来每 件事发生的概率上。事实上，从当前一件事的发生转变到受其影响的接下来的另一件事的发 生，如果这样一个转变过程仅与当前这件事有关，这样就产生了一个简单的马尔可夫过程。 下面举一个简单的例子加以说明，如果我好好复习准备考试周，各门功课都拿到A的概率 是0.6：经过一般准备各门功课都拿到A的概率是0.3：而不好好复习，各门功课都拿到A 的概率是0.1。显然，这样的假设基于：我各门功课最终是否都能拿到A仅与当前我是否认 真准备考试周有关。另一方面，假如我各门功课都能拿到A,我暑假期间选择和同学一起去 旅游的概率为0.6，而选择上小学期的概率为0.4：假如我没能各门功课都拿到A,暑假期间 和同学一起去旅游的概率是0.3，而上小学期的概率则为0.7。显然，此时我们的假设基于： 我暑假是和同学出去旅游还是上小学期仅与我各门功课是否都拿到A有关。从我是否好好 准备考试周的当前状态一直转移到暑假我是和同学出去旅游还是上小学期的将来状态，这样 一整个过程就是一个简单的马尔可夫过程。 如果记我好好复习准备考试周为事件A,作一般准备为事件B,而不好好准备为事件 C,则2(A,B,C)组成了当前所有可能的事件空间。若记我所有课程都拿到A为事件D, 未能所有课程都拿A为事件D,则由题意，知： P(D|A)=0.6,P(D1B)=0.3,P(D|C)=0.1 (1) 又由我各门功课都拿到A和不能都拿到A为互斥事件，故有：

《随机模拟方法与应用》课程大作业 2015 年度 春季学期 1 对 MCMC 方法在瑞利分布样本采集及一元线性回归模型参 数估计中应用的思考与研究 学号：5110109140 姓名：吴凯斌 授课老师：肖柳青 1.全文内容概要 本文基于统计学中有关瑞利分布及一元线性回归分析的参考文献，主要对马尔可夫链蒙 特卡罗方法（即 MCMC 方法）在瑞利分布样本采集以及一元线性回归模型参数估计中的应 用进行了思考与研究。全文共分为三大部分：首先，简单介绍了马尔科夫链的数学概念，并 通过提出一个具体的模型来说明其表示方法；其次，介绍了 MCMC 方法在电子工程中常用 的一个数学分布——瑞利分布中随机采集若干个样本的具体应用，并将算法通过 matlab 加 以实现；最后，介绍了 MCMC 算法在一元线性回归模型参数估计中的应用思想，并将其与 最小二乘法进行了对比。 2.马尔可夫链的概念及其表示方式 无论是世界上重大的政治局势变化，还是我们每个人生活中的一些非常琐碎的事情，它 们之间绝大多数都是有着一定的因果关系的，也就是说每件事情的发生都会对接下来出现的 事情产生一定的影响，这种影响可以是有形的，也可以是无形的，其最终将反映到接下来每 件事发生的概率上。事实上，从当前一件事的发生转变到受其影响的接下来的另一件事的发 生，如果这样一个转变过程仅与当前这件事有关，这样就产生了一个简单的马尔可夫过程。 下面举一个简单的例子加以说明，如果我好好复习准备考试周，各门功课都拿到 A 的概率 是 0.6；经过一般准备各门功课都拿到 A 的概率是 0.3；而不好好复习，各门功课都拿到 A 的概率是 0.1。显然，这样的假设基于：我各门功课最终是否都能拿到 A 仅与当前我是否认 真准备考试周有关。另一方面，假如我各门功课都能拿到 A，我暑假期间选择和同学一起去 旅游的概率为 0.6，而选择上小学期的概率为 0.4；假如我没能各门功课都拿到 A，暑假期间 和同学一起去旅游的概率是 0.3，而上小学期的概率则为 0.7。显然，此时我们的假设基于： 我暑假是和同学出去旅游还是上小学期仅与我各门功课是否都拿到 A 有关。从我是否好好 准备考试周的当前状态一直转移到暑假我是和同学出去旅游还是上小学期的将来状态，这样 一整个过程就是一个简单的马尔可夫过程。 如果记我好好复习准备考试周为事件 A ，作一般准备为事件 B ，而不好好准备为事件 C ，则( , , ) A B C 组成了当前所有可能的事件空间。若记我所有课程都拿到 A 为事件 D ， 未能所有课程都拿 A 为事件 D ，则由题意，知： P D A P D B P D C ( | ) 0.6, ( | ) 0.3, ( | ) 0.1    （1） 又由我各门功课都拿到 A 和不能都拿到 A 为互斥事件，故有：

《随机模拟方法与应用》课程大作业 2015年度春季学期 P(D|A)=0.4,P(D|B)=0.7,P(D1C)=0.9 (2) 同样由于是互斥事件，若设暑假我和同学一起旅游为事件E,则上小学期为事件E。 若记我所得成绩的事件集合为：G(D,D),暑期所做的事件集合为：(E,瓦)。那么： 2(A,B,C)→oD,D→0E,E) (3) 这样一整个转移过程即为马尔可夫链，不难发现，在整个转移过程中，决定事件走向， 或者说决定马尔可夫链走向的关键就是其转移概率。 马尔科夫链的精髓，其实就是简化了系统从一个时刻到下一个时刻的随机演化方式，也就是 假定系统的下一步状态仅取决于当前时刻的系统状态，而与其整个发展历史无关，或者说， 马尔可夫链具有遗忘性。 马尔科夫链也可以用转移矩阵的形式来表示，以上面的模型为例，则转移矩阵的形式如 下： E 0.6 0.4 (4) E 0.3 0.7D 而其中，又有： A D 0.6 0.3 0. (5) D 0.4 0.7 0.9 C 观察可知， 转移矩阵中每一行之和均满足归一性条件：∑P=1。 3.MCMC方法在瑞利分布中采集样本的应用 3.1瑞利分布简介 瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接收包括统计时 变特性的一种分布类型。当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态 分布时，这个向量的模呈瑞利分布，其在电子工程、通信系统等学科中有着极为广泛的应用。 因此，对其进行相关研究是非常有必要的。 3.2瑞利分布 若能机变量X的分布商数影式为：F闲=1-ep-.其中≥0.0>0。 则称随机变量服从瑞利分布，同时不难看出其对应的密度函数为：)=二ep( 3.3特征数 2

《随机模拟方法与应用》课程大作业 2015 年度 春季学期 2 P D A P D B P D C ( | ) 0.4, ( | ) 0.7, ( | ) 0.9    （2） 同样由于是互斥事件，若设暑假我和同学一起旅游为事件 E ，则上小学期为事件 E 。 若记我所得成绩的事件集合为： ( , ) D D ，暑期所做的事件集合为： ( , ) E E 。那么：    ( , , ) , ( , ) A B C D D E E     （3） 这样一整个转移过程即为马尔可夫链，不难发现，在整个转移过程中，决定事件走向， 或者说决定马尔可夫链走向的关键就是其转移概率。 马尔科夫链的精髓，其实就是简化了系统从一个时刻到下一个时刻的随机演化方式，也就是 假定系统的下一步状态仅取决于当前时刻的系统状态，而与其整个发展历史无关，或者说， 马尔可夫链具有遗忘性。 马尔科夫链也可以用转移矩阵的形式来表示，以上面的模型为例，则转移矩阵的形式如 下： 0.6 0.4 0.3 0.7 E D E D                            （4） 而其中，又有： 0.6 0.3 0.1 0.4 0.7 0.9 A D B D C                            (5) 观察可知，转移矩阵中每一行之和均满足归一性条件： 1 ij   p 。 3.MCMC 方法在瑞利分布中采集样本的应用 3.1 瑞利分布简介 瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接收包括统计时 变特性的一种分布类型。当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态 分布时，这个向量的模呈瑞利分布，其在电子工程、通信系统等学科中有着极为广泛的应用。 因此，对其进行相关研究是非常有必要的。 3.2 瑞利分布 若随机变量 X 的分布函数形式为： 2 2 ( ) 1 exp( ) 2 x F x      ，其中 x   0, 0  。 则称随机变量服从瑞利分布，同时不难看出其对应的密度函数为： 2 2 2 ( ) exp( ) 2 x x f x     。 3.3 特征数

《随机模拟方法与应用》课程大作业 2015年度春季学期 x=fh-j亭p -r -2 -x2 =-∫xde2a)=-xe2a+∫e2dk (6) 2J√2πb Ex-Jxx exp(x =-rde)=-e6+2jeh (7) =-2b2∫de2a)=2o2 Dx-EX-(EXY-2- (8) 3.4参数的极大似然估计 似然函数为： L(a)=e (9) 对数似然函数为： x h4o)=-2mlna+宫n-2a (10) 对上式求导，得： dInL(o)2n +1 (11) do 令上式为0，得参数的极大似然估计为： (12) 2n 3.5MCMC方法在瑞利分布中随机采集样本的应用及matlab模拟 3

《随机模拟方法与应用》课程大作业 2015 年度 春季学期 3 2 2 2 2 2 2 2 2 2 2 2 0 0 2 2 2 0 0 0 2 ( ) exp( ) 2 ( ) | 2 1 2 2 2 x x x x x x EX xf x dx x dx xd e xe e dx b e dx b b                                    （6） 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 0 0 0 2 2 2 0 exp( ) 2 ( ) | 2 2 ( ) 2 x x x x x x EX x dx x d e x e xe dx b d e                               （7） 2 2 2 2 2 4 ( ) 2 ( ) 2 2 DX EX EX            （8） 3.4 参数的极大似然估计 似然函数为： 2 2 2 2 2 2 2 2 1 1 ( ) i i x x n n i n i i i x L e x e               （9） 对数似然函数为： 2 1 2 1 ln ( ) 2 ln ln 2 n n i i i i x L n x            （10） 对上式求导，得： 2 1 3 ln ( ) 2 n i i x d L n d         （11） 令上式为 0，得参数的极大似然估计为： 2 1 2 2 n i i x n    。 （12） 3.5 MCMC 方法在瑞利分布中随机采集样本的应用及 matlab 模拟

《随机模拟方法与应用》课程大作业 2015年度春季学期 -x2 考忠如下瑞利分布，其概率密度面数为：)产后，我首先考志了从该分 布中随机产生l000个样本来近似该概率密度分布函数的情形，若取总循环次数total number 为500,000，g=1,每隔500次收集一次，共得到最终样本数为1000。其matlab源代码如 下： c1eara11;号5110109140吴凯斌《随机模拟方法与应用》大作业程序辅导老师：肖柳青 close all; sigma=l；号给定分布中sigma的数值 j=1; total Num=500000; 号定义模拟总次数和样本总数 sample num=5000; sample=zeros(1,total Num); 号设置样本存储空间 =5*rand(1); sample(j)=x; for i=1:total Num 号设置建议密度函数 &fy=1/sqrt (2*pi)*exp(-(y-x)2/2) z=randn(1)+sample(j); u=rand(1); 号计算alpha的值，alpha=pi(y)*g(y,x)/(pi()*g(,y) 1f(z>=0) alpha=z/sigma2*exp(-z2/2/sigma2)/(sample(j)/sigma2*exp (-sample (j) ^2/2/sigma^2)); else alpha=0; end alpha=min(1,alpha); if(u<=alpha) sample(j+1)=z; else sample(j+1)=sample(j); end j=j+1; 4

《随机模拟方法与应用》课程大作业 2015 年度 春季学期 4 考虑如下瑞利分布，其概率密度函数为： 2 2 2 ( ) exp( ) 2 x x f x     ，我首先考虑了从该分 布中随机产生 1000 个样本来近似该概率密度分布函数的情形，若取总循环次数 total_number 为 500,000， 1，每隔 500 次收集一次，共得到最终样本数为 1000。其 matlab 源代码如 下： clear all; %5110109140_吴凯斌 《随机模拟方法与应用》大作业程序 辅导老师：肖柳青 close all; sigma=1; %给定分布中sigma的数值 j=1; total_Num=500000; %定义模拟总次数和样本总数 sample_num=5000; sample=zeros(1,total_Num); %设置样本存储空间 x=5*rand(1); sample(j)=x; for i=1:total_Num %设置建议密度函数 %fy=1/sqrt(2*pi)*exp(-(y-x)^2/2) z=randn(1)+sample(j); u=rand(1); %计算alpha的值, alpha=pi(y)*q(y,x)/(pi(x)*q(x,y)) if(z>=0) alpha=z/sigma^2*exp(-z^2/2/sigma^2)/(sample(j)/sigma^2*exp(-sample(j) ^2/2/sigma^2)); else alpha=0; end alpha=min(1,alpha); if(u<=alpha) sample(j+1)=z; else sample(j+1)=sample(j); end j=j+1;

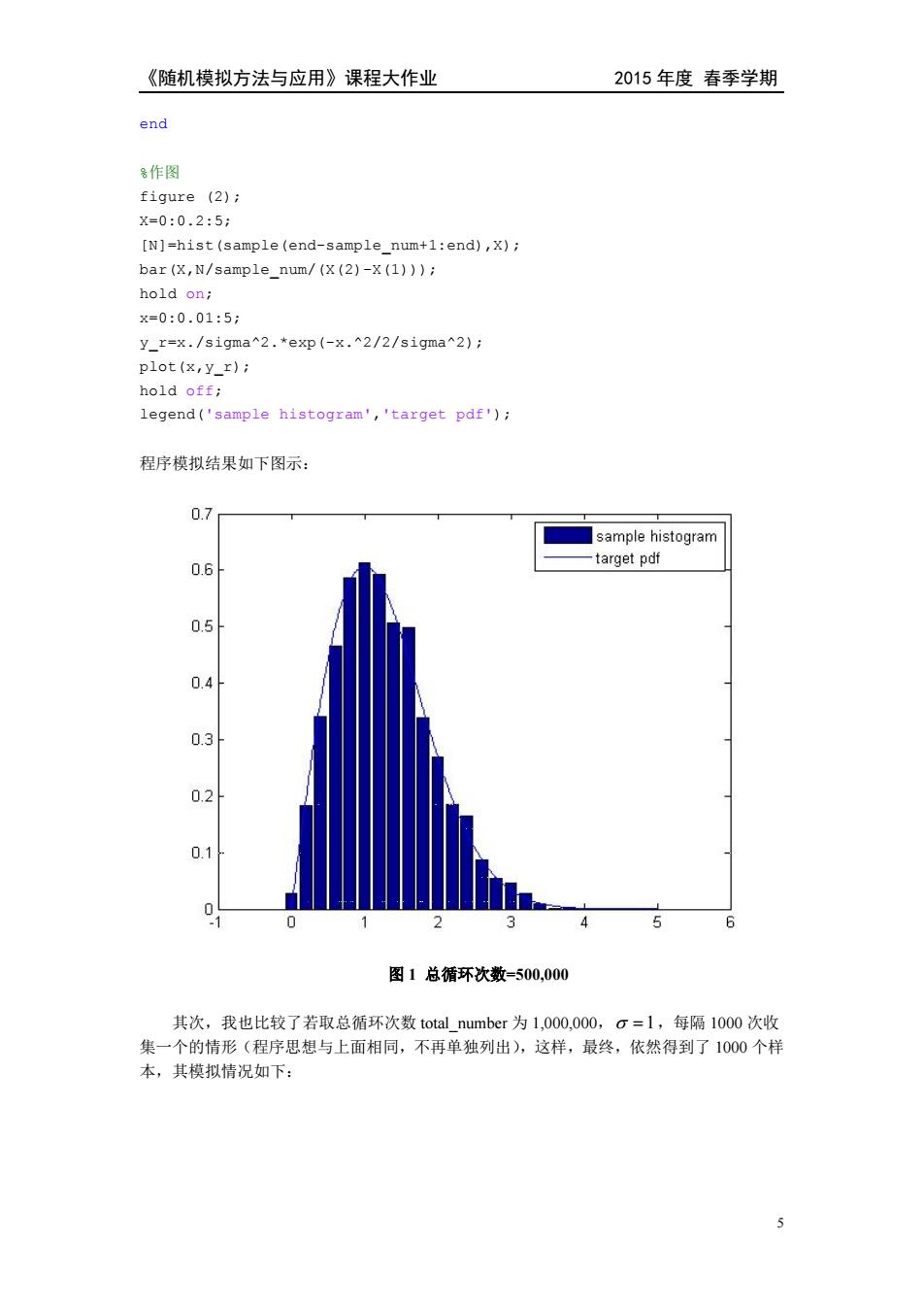
《随机模拟方法与应用》课程大作业 2015年度春季学期 end 各作图 figure (2); X=0:0.2:5; [N]=hist (sample(end-sample_num+1:end),x); bar(X,N/sample_num/(X (2)-x (1))); hold on; x=0:0.015; y_r=x./sigma2.*exp (-x.2/2/sigma2) plot(x,y_r); hold off; legend('sample histogram','target pdf'); 程序模拟结果如下图示： 0.7 ■sample histogram 0.6 target pdf 0.5 0.4 0.3 0.2 0.1 0 -1 0 3 6 图1总循环次数=500,000 其次，我也比较了若取总循环次数total number为1,000,000，g=1,每隔1000次收 集一个的情形（程序思想与上面相同，不再单独列出），这样，最终，依然得到了1000个样 本，其模拟情况如下： 5

《随机模拟方法与应用》课程大作业 2015 年度 春季学期 5 end %作图 figure (2); X=0:0.2:5; [N]=hist(sample(end-sample_num+1:end),X); bar(X,N/sample_num/(X(2)-X(1))); hold on; x=0:0.01:5; y_r=x./sigma^2.*exp(-x.^2/2/sigma^2); plot(x,y_r); hold off; legend('sample histogram','target pdf'); 程序模拟结果如下图示： 图 1 总循环次数=500,000 其次，我也比较了若取总循环次数 total_number 为 1,000,000， 1，每隔 1000 次收 集一个的情形（程序思想与上面相同，不再单独列出），这样，最终，依然得到了 1000 个样 本，其模拟情况如下：