
1.连通图 2 路径:从图的某一结点出 发,沿着一些支路连续移 5 动,从而到达另一指定的 3 节点(或回到原出发点), 3 这样的一系列支路构成了图G的一条 路径。一条支路本身也是一条路径。 ·当图G的任意两个 结点之间至少存在 一条路径时,G就 称为连通图。 连通图 非连通图 2025年4月2日星期三 11
2025年4月2日星期三 11 1. 连通图 • 当图G的任意两个 结点之间至少存在 一条路径时,G就 称为连通图。 ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ 路径:从图的某一结点出 发,沿着一些支路连续移 动,从而到达另一指定的 节点 (或回到原出发点), 这样的一系列支路构成了图G的一条 路径。一条支路本身也是一条路径。 连通图 非连通图

若一条路径的起点和终点重 (1,2,6,8) 2 合,且经过的其它结点都相 I 异,则这条闭合路径就构成 了图G的一个回路。 8 (1,5,8),(2,5,6),(1,2,3,4)/3,4,8,6) 。 共有13个不同的回路,但独 立回路数远小于13个。 由2个可得第3个。 ③不包含回路。 2.树(Tree)的定义 构成树的各支路叫 一个连通图G的树T, 树支,如5,6,7,8。 ①包含G的全部结点; 其余支路叫连支, ②本身是连通的; 如1,2,3,4。 2025年4月2日星期三 12
2025年4月2日星期三 12 若一条路径的起点和终点重 合,且经过的其它结点都相 异,则这条闭合路径就构成 了图G的一个回路。 • 共有13个不同的回路,但独 立回路数远小于13个。 2. 树 (Tree)的定义 一个连通图G的树T, ①包含G的全部结点; ②本身是连通的; ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ (1,5,8),(2,5,6),(1,2,3,4), 构成树的各支路叫 树支,如5,6,7,8。 其余支路叫连支, 如1,2,3,4。 ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ (3,4,8,6) (1,2,6,8) 由2个可得第3个。 ③不包含回路
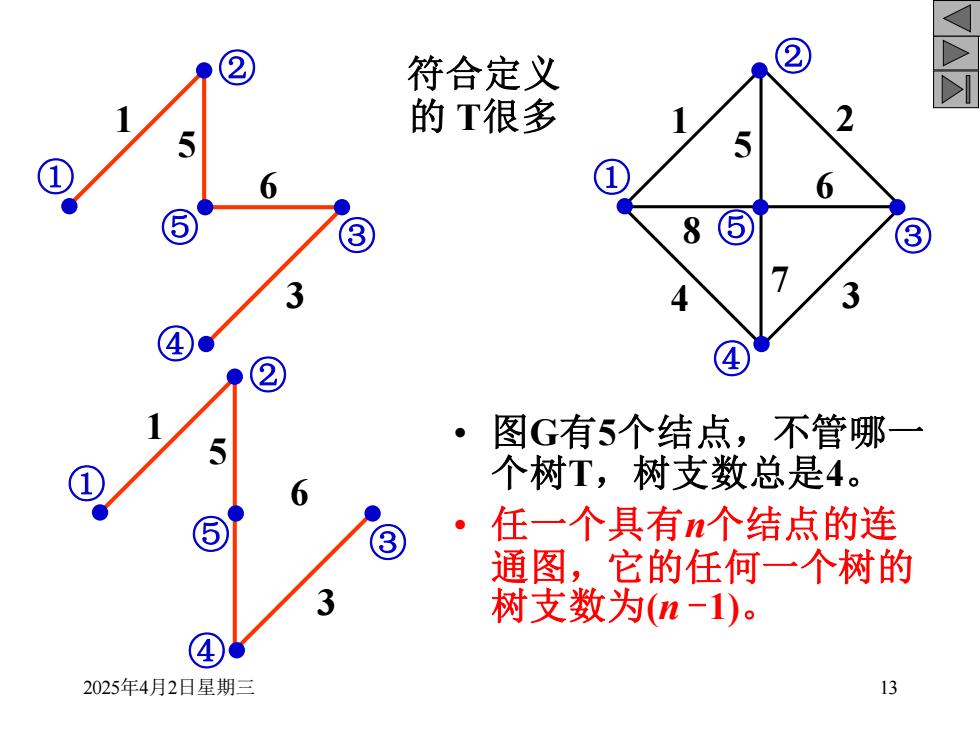
② 符合定义 ② 的T很多 2 5 5 ① 6 6 ⑤ ③ 8 ③ 3 A 3 ④ ② 图G有5个结点,不管哪一 5 个树T,树支数总是4。 ③ ·任一个具有n个结点的连 通图,它的任何一个树的 树支数为(n-1)。 ④ 2025年4月2日星期三 13
2025年4月2日星期三 13 ① 1 3 5 6 ② ③ ④ ⑤ ① 1 3 5 6 ② ③ ④ ⑤ 符合定义 的 T很多 ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ • 图G有5个结点,不管哪一 个树T,树支数总是4。 • 任一个具有n个结点的连 通图,它的任何一个树的 树支数为(n -1)

2 2 5 8 ⑤ 5 D 3 ④ 含回路 5 6 ● 8 ⑤ ③ 不连通 ④· 2025年4月2日星期三 14
2025 年 4 月 2日星期三 14 ① 2 5 6 7 8 ② ③ ④⑤ ① 5 6 8 ② ③ ④⑤ 含回路 不连通 ① 1 2 4 3 5 6 7 8 ② ③ ④⑤
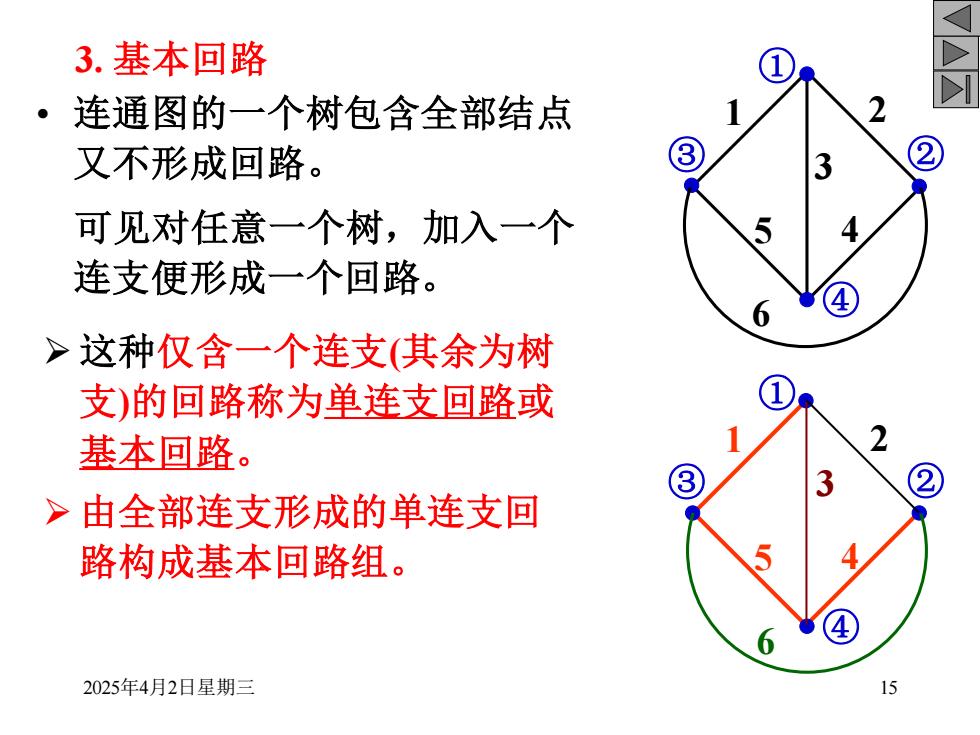
3.基本回路 连通图的一个树包含全部结点 又不形成回路。 可见对任意一个树,加入一个 连支便形成一个回路。 4 > 这种仅含一个连支(其余为树 支)的回路称为单连支回路或 基本回路。 3 >由全部连支形成的单连支回 路构成基本回路组。 4 2025年4月2日星期三
2025年4月2日星期三 15 3. 基本回路 • 连通图的一个树包含全部结点 又不形成回路。 可见对任意一个树,加入一个 连支便形成一个回路。 ➢ 这种仅含一个连支(其余为树 支)的回路称为单连支回路或 基本回路。 ➢ 由全部连支形成的单连支回 路构成基本回路组。 ① ③ ② ④ 1 2 3 5 4 6 ① ③ ② ④ 1 5 4 2 6 3