
第十五章电路方程的矩阵形式 结束 重点 1.掌握割集的概念,熟练写出电路关联矩阵 A、回路矩阵B、割集矩阵Q; 2.掌握复合支路的概念; 3.学会用矩阵形式列写回路电流方程、结点 电压方程和割集电压方程; 难点 割集电压方程的列写。 2025-4-2 1
结束 第十五章 电路方程的矩阵形式 1. 掌握割集的概念,熟练写出电路关联矩阵 A、回路矩阵B、割集矩阵Q; 2. 掌握复合支路的概念; 3. 学会用矩阵形式列写回路电流方程、结点 电压方程和割集电压方程; 重点 难点 割集电压方程的列写。 2025-4-2 1

1.连通图 从图的某一结点出发,沿 结束 着一些支路连续移动,从 而到达另一指定的节点 (或回到原出发点), 这样的一系列支路构成了图G的一条 路径。一条支路本身也是一条路径。 。 当图G的任意两个 结点之间至少存在 一条路径时,G就 称为连通图。 连通图 非连通图 2025-4-2 2
结束 1. 连通图 • 当图G的任意两个 结点之间至少存在 一条路径时,G就 称为连通图。 ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ 从图的某一结点出发,沿 着一些支路连续移动,从 而到达另一指定的节点 (或回到原出发点), 这样的一系列支路构成了图G的一条 路径。一条支路本身也是一条路径。 连通图 非连通图 2025-4-2 2
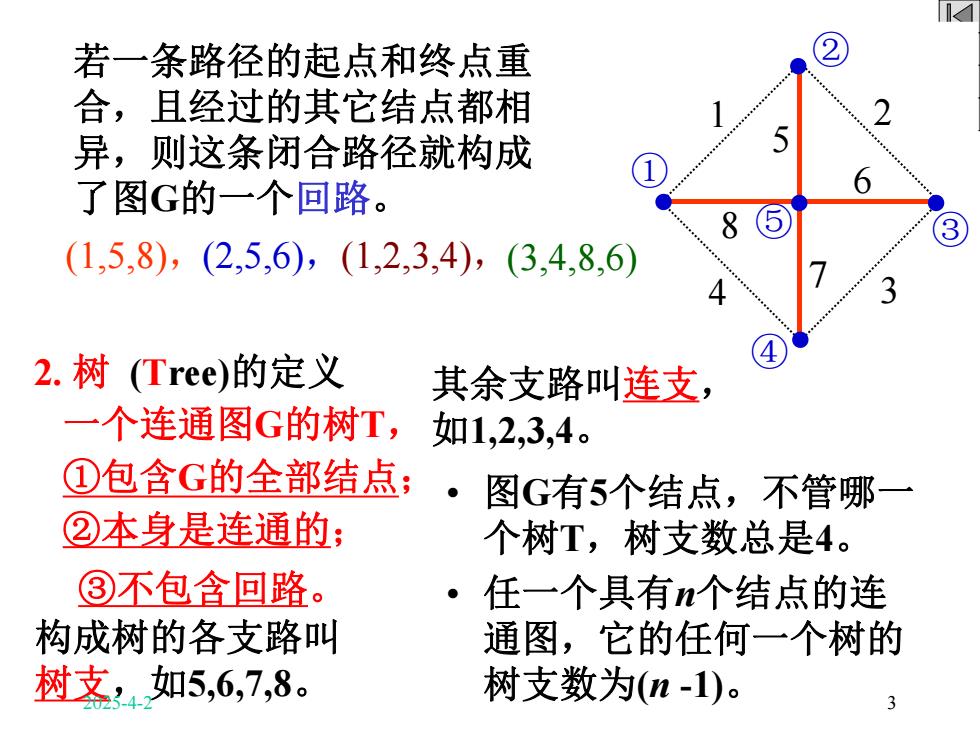
若一条路径的起点和终点重 合,且经过的其它结点都相 异,则这条闭合路径就构成 了图G的一个回路。 (1,5,8),(2,5,6),(1,2,3,4),(3,4,8,6) 2.树(Tree)的定义 其余支路叫连支, 一个连通图G的树T, 如1,2,3,4。 ①包含G的全部结点;· 图G有5个结点,不管哪一 ②本身是连通的: 个树T,树支数总是4。 ③不包含回路。 。 任一个具有n个结点的连 构成树的各支路叫 通图,它的任何一个树的 树支,如5,6,7,8。 树支数为(n-1)
结束 若一条路径的起点和终点重 合,且经过的其它结点都相 异,则这条闭合路径就构成 了图G的一个回路。 2. 树 (Tree)的定义 一个连通图G的树T, ①包含G的全部结点; ②本身是连通的; ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ (1,5,8),(2,5,6),(1,2,3,4), 构成树的各支路叫 树支,如5,6,7,8。 ① 1 2 4 3 5 6 7 8 ② ③ ④ ⑤ (3,4,8,6) ③不包含回路。 • 图G有5个结点,不管哪一 个树T,树支数总是4。 • 任一个具有n个结点的连 通图,它的任何一个树的 树支数为(n -1)。 其余支路叫连支, 如1,2,3,4。 2025-4-2 3
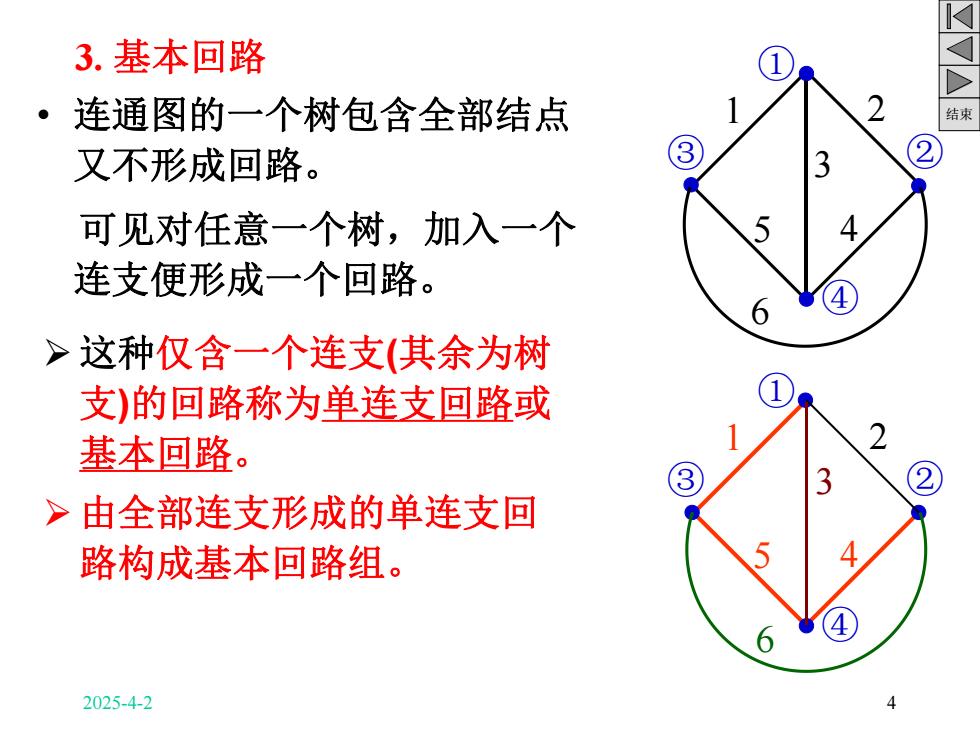
3.基本回路 ·连通图的一个树包含全部结点 结束 又不形成回路。 可见对任意一个树,加入一个 连支便形成一个回路。 >这种仅含一个连支(其余为树 支)的回路称为单连支回路或 基本回路。 >由全部连支形成的单连支回 路构成基本回路组。 2025-4-2
结束 3. 基本回路 • 连通图的一个树包含全部结点 又不形成回路。 可见对任意一个树,加入一个 连支便形成一个回路。 Ø 这种仅含一个连支(其余为树 支)的回路称为单连支回路或 基本回路。 Ø 由全部连支形成的单连支回 路构成基本回路组。 ① ③ ② ④ 1 2 3 5 4 6 ① ③ ② ④ 1 5 4 2 6 3 2025-4-2 4
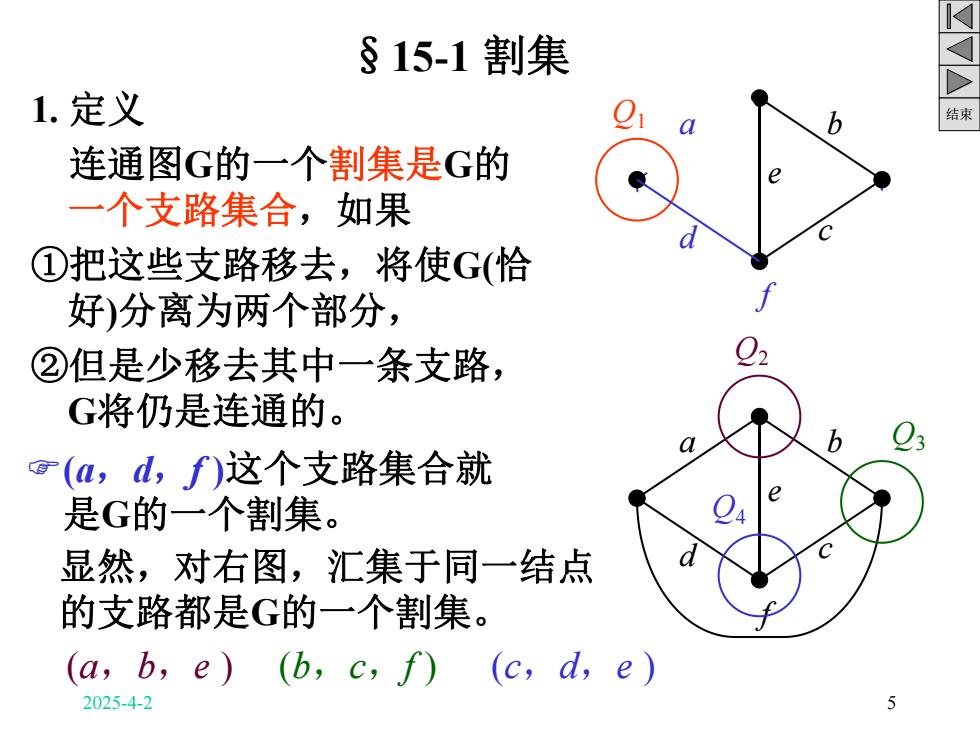
§15-1割集 1.定义 结束 连通图G的一个割集是G的 e 一个支路集合,如果 ①把这些支路移去,将使G(恰 好)分离为两个部分, ②但是少移去其中一条支路, G将仍是连通的。 g(a,d,f)这个支路集合就 是G的一个割集。 显然,对右图,汇集于同一结点 的支路都是G的一个割集。 (a,b,e)(b,c,f)(c,d,e) 2025-4-2 5
结束 §15-1 割集 1. 定义 连通图G的一个割集是G的 一个支路集合,如果 ①把这些支路移去,将使G(恰 好)分离为两个部分, ②但是少移去其中一条支路, G将仍是连通的。 F(a,d,f )这个支路集合就 是G的一个割集。 a d f b c e Q1 a d f b c e Q2 Q3 Q4 (a,b,e ) (b,c,f ) (c,d,e ) 显然,对右图,汇集于同一结点 的支路都是G的一个割集。 2025-4-2 5