举例:已知:A = 40 0.1, A, = 20t01, A, = 59.5-04极值法:皖A.=0.5187概率法-A340TAUJ.按对称公差计算:2+0. 1-(-0. 4)=0. 7EIAo=EIA,+EIA2-ESA3=0. 1+0-(-0. 1)=0. 2. Ag = 0.5t02A, = A, + Az - A, = 40.15 + 20.05 - 59.25 = 0.95AAoT = /0.12 + 0.12 + 0.32 ~ 0.332: Ao = 0.95 ± 0.17 = 0.5±0.62A+0.28
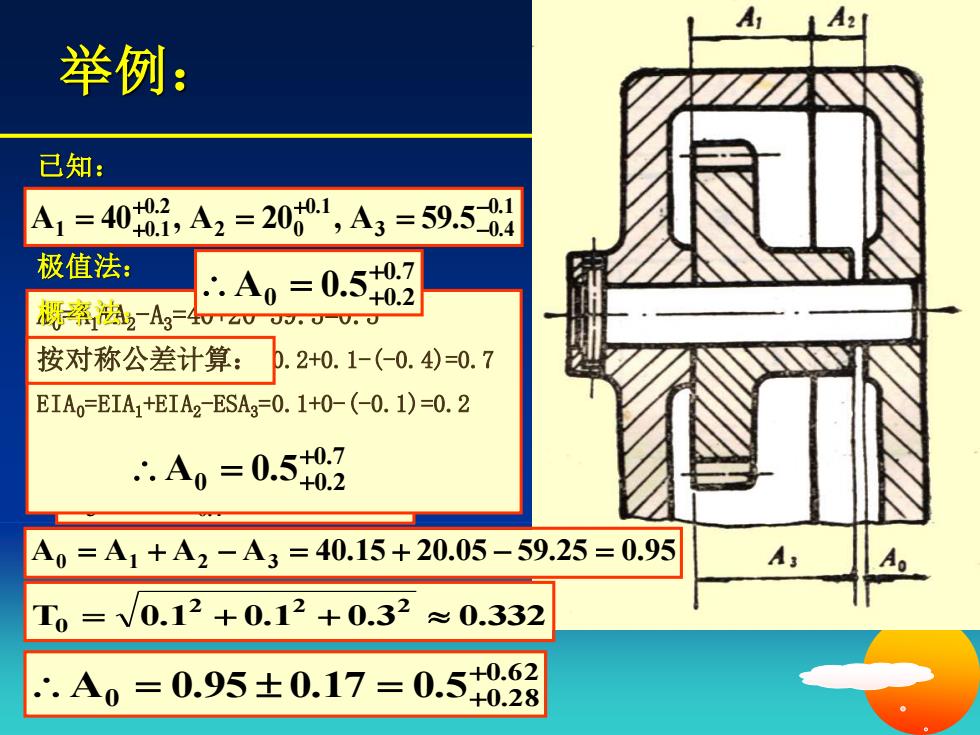
A 59.5 59.25 0.15 A 20 20.05 0.05 A 40 40.15 0.05 0.1 3 0.4 0.1 2 0 0.2 1 0.1 = = = = = = − − + + + A0=A1+A2-A3=40+20-59.5=0.5 ESA0=ESA1+ESA2-EIA3=0.2+0.1-(-0.4)=0.7 EIA0=EIA1+EIA2-ESA3=0.1+0-(-0.1)=0.2 0.7 0 5 0.2 A 0. + = + 举例: 已知: 0.1 3 0.4 0.1 2 0 0.2 1 0.1 A 40 , A 20 , A 59.5 − − + + = + = = 极值法: 概率法: 按对称公差计算: A0 = A1 + A2 − A3 = 40.15 + 20.05 − 59.25 = 0.95 T 0.1 0.1 0.3 0.332 2 2 2 0 = + + 0.6 2 0 5 0.2 8 A 0.95 0.17 0. + = = + 0.7 0 5 0.2 A 0. + = +

反计算问题由国标:T=ai10.45×3/D+0.001×DD≤500mm1.等公差法D>500~3150mm0.004× D+2.1极值法:To其中:a:公差等级i:公差单位概率法:ToD:基本尺寸D= /D, ×D22.等精度法T/DT.3DT极值法:概率法:mD2/3≥/D一3.经验法根据加工难易程度分配极值法:根据加工难易程度分配概率法:mmT2公差满足:T=ZT公差满足:T。i=li-l
反计算问题: 1. 等公差法 极值法: m T T T Ti m i i 0 1 0 = = = 概率法: m T m m T T T Ti m i i 0 0 1 2 0 = = = = m:组成环数 2. 等精度法 = = m i i i i D T D T 1 3 3 0 极值法: 概率法: = = m i i i i D T D T 1 2 3 3 0 3. 经验法 极值法: = = m i T Ti 1 公差满足: 0 根据加工难易程度分配 概率法: = = m i T Ti 1 2 公差满足: 0 根据加工难易程度分配 由国标:T=a·i 其中:a:公差等级 i:公差单位 D:基本尺寸 + + = D D mm i D D D mm 0.004 2.1 500 ~ 3150 0.45 0.001 500 3 D = D1 D2