
二、一阶系统的单位阶跃响应 X(s)=G(s)X;(s) X,(s)=L[(t】=- S 1 X,(s)=G(S)X,(S)= Ts+1 s x()=L'[X,(s]=E'[ S xou(t)=1-e-i/T e/T为瞬态项,1为稳态项B(t) -
二 、 一阶系统的单位阶跃响应 1 ( ) ( ) 1 ] 1 1 1 ( ) [ ( )] [ 1 1 1 ( ) ( ) ( ) 1 ( ) [ ( )] ( ) ( ) ( ) / / 1 1 e B t x t e Ts s x t L X s L Ts s X s G s X s s X s L u t X s G s X s t T t T o u o u o o i i o i − 为瞬态项,为稳态项 − − − − = − • + = = • + = = = = = 1 ( ) ( ) 1 ] 1 1 1 ( ) [ ( )] [ 1 1 1 ( ) ( ) ( ) 1 ( ) [ ( )] ( ) ( ) ( ) / / 1 1 e B t x t e Ts s x t L X s L Ts s X s G s X s s X s L u t X s G s X s t T t T o u o u o o i i o i − 为瞬态项,为稳态项 − − − − = − • + = = • + = = = = = 1 ( ) ( ) 1 ] 1 1 1 ( ) [ ( )] [ 1 1 1 ( ) ( ) ( ) 1 ( ) [ ( )] ( ) ( ) ( ) / / 1 1 e B t x t e Ts s x t L X s L Ts s X s G s X s s X s L u t X s G s X s t T t T o u o u o o i i o i − 为瞬态项,为稳态项 − − − − = − • + = = • + = = = = = 1 ( ) ( ) 1 ] 1 1 1 ( ) [ ( )] [ 1 1 1 ( ) ( ) ( ) 1 ( ) [ ( )] ( ) ( ) ( ) / / 1 1 e B t x t e Ts s x t L X s L Ts s X s G s X s s X s L u t X s G s X s t T t T o u o u o o i i o i − 为瞬态项,为稳态项 − − − − = − • + = = • + = = = = = 1 ( ) ( ) 1 ] 1 1 1 ( ) [ ( )] [ 1 1 1 ( ) ( ) ( ) 1 ( ) [ ( )] ( ) ( ) ( ) / / 1 1 e B t x t e Ts s x t L X s L Ts s X s G s X s s X s L u t X s G s X s t T t T o u o u o o i i o i − 为瞬态项,为稳态项 − − − − = − • + = = • + = = = = =
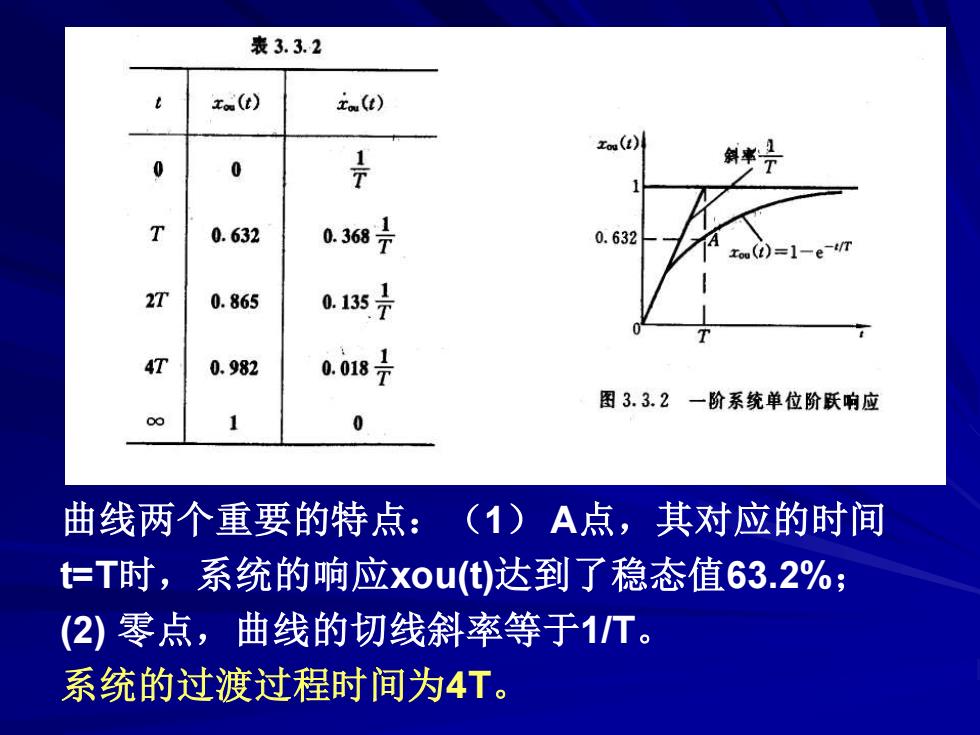
表3.3.2 z(t) i.(t) Zou(t) 0 0 2 0.632 0.3687 0.632 Iou(t)=1-e-i/T 2T 0.865 01357 4T 0.982 a.018号 图3.3.2一阶系统单位阶跃响应 0 曲线两个重要的特点: (1)A点,其对应的时间 t=T时,系统的响应xou()达到了稳态值63.2%; (2)零点,曲线的切线斜率等于1T。 系统的过渡过程时间为4T
曲线两个重要的特点:(1) A点,其对应的时间 t=T时,系统的响应xou(t)达到了稳态值63.2%; (2) 零点,曲线的切线斜率等于1/T。 系统的过渡过程时间为4T

3.4二阶系统 2 Xo(s) G(S)= Xi(s) s2+250nS+0n 式中, o, 称为无阻尼固有频率, 5称为阻尼比。 它们是二阶系统的特征参数,表明系统本 身的固有特性
3.4 二阶系统 式中, 称为无阻尼固有频率, 称为阻尼比。 它们是二阶系统的特征参数,表明系统本 身的固有特性。 2 2 2 ( ) 2 ( ) ( ) n n n Xi s s s Xo s G s + + = = n

二阶系统的特征方程为 +25w,s+0,2=0 2 此方程的两个特征根为 S2=-50,±0N52-1
二阶系统的特征方程为 此方程的两个特征根为 2 0 2 2 s + n s +n = 1 2 s1,2 = − n n −

阻尼比取不同的值,二阶系统的特征根也不同 (1)当0<ξ<1时,两特征根为共轭复数,即 S2=-50,±j0V1-52 欠阻尼系统。 (2)当5=0时,两特征根为共轭纯虚根,即 S12=±jwn 无阻尼系统。 (3)当ξ=1时, 两特征根为相等的负实根,即 S1,2 临界阻尼系统。 (4)当》1时,两特征根为不相等的负实根,即 S2=-50,±0nV52-1 过阻尼系统
阻尼比取不同的值,二阶系统的特征根也不同 (1)当0<ξ<1时,两特征根为共轭复数,即 欠阻尼系统。 (2)当ξ=0时,两特征根为共轭纯虚根,即 无阻尼系统。 (3)当ξ=1时,两特征根为相等的负实根,即 临界阻尼系统。 (4)当ξ〉1时,两特征根为不相等的负实根,即 过阻尼系统。 2 1,2 = − 1− n n s j n s1,2 = j n s1,2 = − 1 2 s1,2 = − n n −