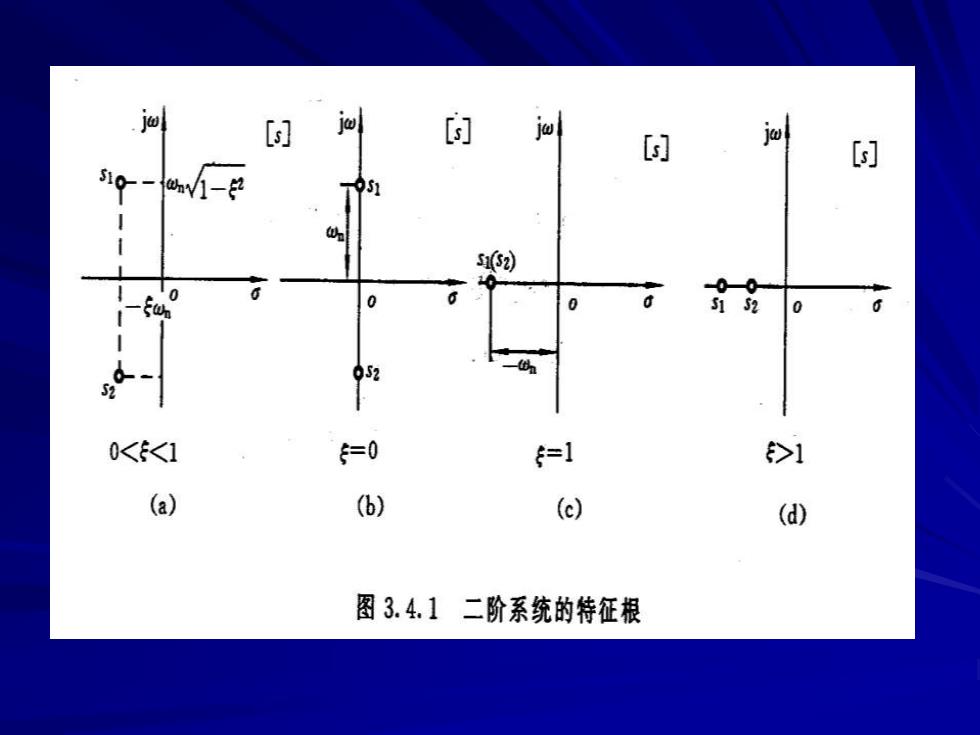
[] [时 [时 [ V-名 5) 0 0 0 052 0<<1 =0 =1 >1 (a) (6) (e) (d) 图3.4.1二阶系统的特征根

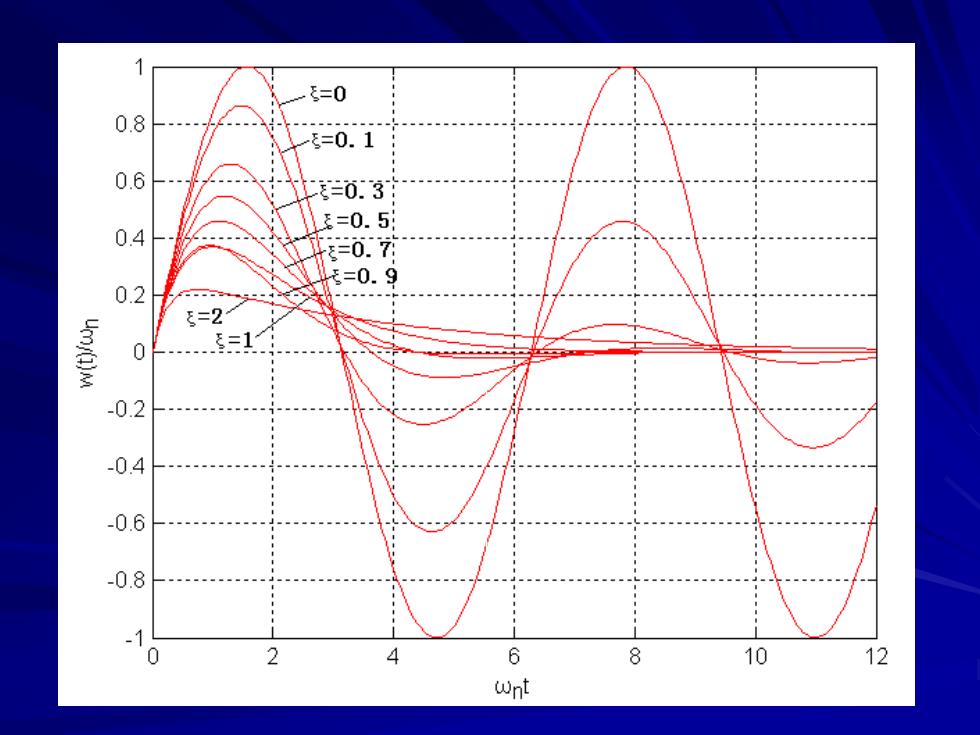
二阶系统的单位脉冲响应 W(s)=Xo(s)=G(s)Xi(s) Xi(s)=L[δ(t)]=1 W(s)=G(s) w0)=1rG(s]=L'[+25o,s+ 2 2 =L[ (s+5@,)2+(oV1-522
一.二阶系统的单位脉冲响应 ] ( ) ( 1 ) [ ] 2 ( ) [ ( )] [ ( ) ( ) ( ) [ ( )] 1 ( ) ( ) ( ) ( ) 2 2 2 2 1 2 2 2 1 1 + + − = + + = = = = = = = − − − n n n n n n s L s s w t L G s L W s G s Xi s L t W s Xo s G s Xi s ] ( ) ( 1 ) [ ] 2 ( ) [ ( )] [ ( ) ( ) ( ) [ ( )] 1 ( ) ( ) ( ) ( ) 2 2 2 2 1 2 2 2 1 1 + + − = + + = = = = = = = − − − n n n n n n s L s s w t L G s L W s G s Xi s L t W s Xo s G s Xi s ] ( ) ( 1 ) [ ] 2 ( ) [ ( )] [ ( ) ( ) ( ) [ ( )] 1 ( ) ( ) ( ) ( ) 2 2 2 2 1 2 2 2 1 1 + + − = + + = = = = = = = − − − n n n n n n s L s s w t L G s L W s G s Xi s L t W s Xo s G s Xi s

(1)当0<飞<1系统欠阻尼时, 0nV1-52 a-r容s+5a+a-y (≥0) e sin @at V1-52 (2)当=0系统无阻尼时, w(t0三0"2十2J=Dnsm (≥0)
(1)当0<ξ<1系统欠阻尼时, (t≥0) (2)当ξ=0系统无阻尼时, (t≥0) e t s w t L d n t n n n n n sin 1 ] ( ) ( 1 ) 1 1 ( ) [ 2 2 2 2 2 2 1 − − − = + + − − − = t s w t L n n n n n ( ) [ ] sin 2 2 1 = + = −

(3)当=1系统临界阻尼时, 0=5o57e (≥0) (4)〉1系统过阻尼时, 1 w(t)= -]-L 2V52-1s+(5-V52-1)o s+(5+V52-1)@n e5-o-e5+o] 2V52-1 欠阻尼系统称为二阶振荡系统,其幅值衰减的快 慢取决于5o, 。 (≥0)
(3)当ξ=1系统临界阻尼时, (t≥0) (4)ξ〉1系统过阻尼时, 欠阻尼系统称为二阶振荡系统,其幅值衰减的快 慢取决于 。(t≥0) t n n n n t e s w t L − − = + = 2 2 2 1 ] ( ) ( ) [ n [ ] 2 1 ] ( 1) 1 ] [ ( 1) 1 [ 2 1 ( ) ( 1) ( 1) 2 2 1 2 1 2 2 2 n t t n n n n n e e s L s w t L − − − − + − − − − − = + + − − − + − − =
=0 0.8 =0.1 0.6 0.31 =0.5 0.4 0.7 =0.9 0.2 5二2 0 .02 .0.4 -0.6 -0.8 0 2 4 6 8 10 12 Wnt