第四章 频率特性分析 §4.1频率特性概述 (t)=Xisinat 一、 频率响应与频率特性 0)=X(sin[t+)] 1、频率响应 酒型 线性定常系统对谐波输 (a 入的稳态响应,称为频 率响应。 (b 图4.1.1系统及稳态的输人输出被形 xo(t)=Xo(o)sin[ot+o(@)]
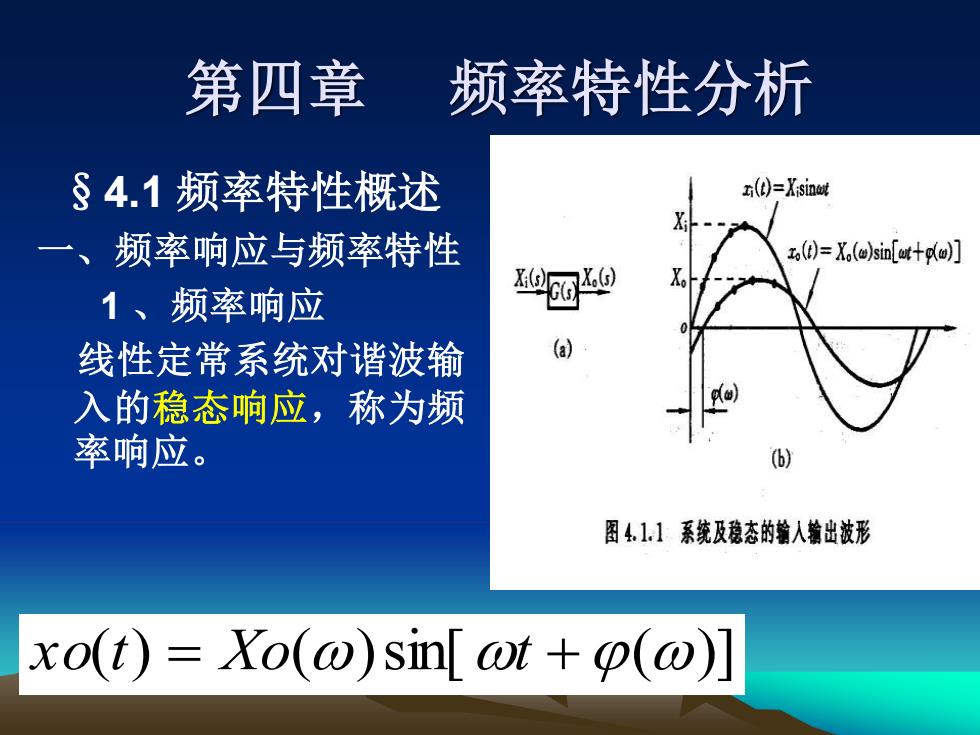
第四章 频率特性分析 §4.1 频率特性概述 一、频率响应与频率特性 1 、频率响应 线性定常系统对谐波输 入的稳态响应,称为频 率响应。 x o(t) = Xo()sin[t +()]

K 例1设传递函数为 G(S)= Ts+1 x;(t)=X;si ot 设输入信号为 X,(S)= X,0 s2+0 2 则输出为 K X,0 X(s)=G(s)X,(S)= Ts+1 s2+@2 X,KT@ X K x,(t)= ●e-tlT sin(ot -arctan To) 1+T2o2 V1+T2@2 系统的稳态响应 X K x,(t)= sin(ot-arctan To) v+T@2
例1 设传递函数为 1 ( ) + = Ts K G s 设输入信号为 2 2 ( ) ( ) sin + = = s X X s x t X t i i i i 则输出为 2 2 1 ( ) ( ) ( ) + • + = = s X Ts K X s G s X s i o i sin( arctan ) 1 1 ( ) 2 2 / 2 2 t T T X K e T X KT x t i t T i o − + • + + = − 系统的稳态响应 sin( arctan ) 1 ( ) 2 2 t T T X K x t i o − + =

系统输出的幅值 XK X(o)三 V1+T202 系统输出的相位 p(o) =-arctan To 频率响应只是时间响应的一个特例。当谐波 频率不同时,其输出的幅值与相位也不同
系统输出的幅值 2 2 1 ( ) T X K X i o + = 系统输出的相位 () = −arctan T 频率响应只是时间响应的一个特例。当谐波 频率不同时,其输出的幅值与相位也不同

2频率特性 幅频特性:线性系统在谐波输入作用下,其稳定输出与输 入的幅值比,即 Xo(@) A(⊙)= X 相频特性:稳态输出信号与输入信号的相位差。 相位逆时针为正,顺时针为负。 相位超前为正,相位滞后为负。 A(o)·∠p(o) 对物理系统相位一般都是滞后的。 幅频特性和相频特性总称为频率特性。 A(o)e()
2 频率特性 幅频特性:线性系统在谐波输入作用下,其稳定输出与输 入的幅值比,即 相频特性:稳态输出信号与输入信号的相位差。 相位逆时针为正,顺时针为负。 相位超前为正,相位滞后为负。 对物理系统相位一般都是滞后的。 幅频特性和相频特性总称为频率特性。 Xi Xo A ( ) ( ) = 记作 A() • () 或 ( ) ( ) j A e

二频率特性与传递函数的关系 设系统的微分方程为: a,x(t)+axmD(t)+.+a&(t)+aoxo(t) =bmxm)(t)+bm1xm-少())+.+b,()+box,() 系统传递函数为 G(S)= Y(s)_bns"+bm-1sm1+.+b3+b。 X,(s) anS”+an-1s++a1S+a。 当输入信号为 x;(t)=X,si ot 即 Xω X,(S)= s2+2
二 频率特性与传递函数的关系 设系统的微分方程为: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 ( 1) 1 ( ) 1 0 ( 1) 1 ( ) b x t b x t b x t b x t a x t a x t a x t a x t i i m m i m m i o o n n o n n o = + + + + + + + + − − − − 系统传递函数为 o n n n n o m m m m i o a s a s a s a b s b s b s b X s X s G s + + + + + + + + = = − − − − 1 1 1 1 1 1 ( ) ( ) ( ) 当输入信号为 x t X t i ( ) = i sin 即 2 2 ( ) + = s X X s i i