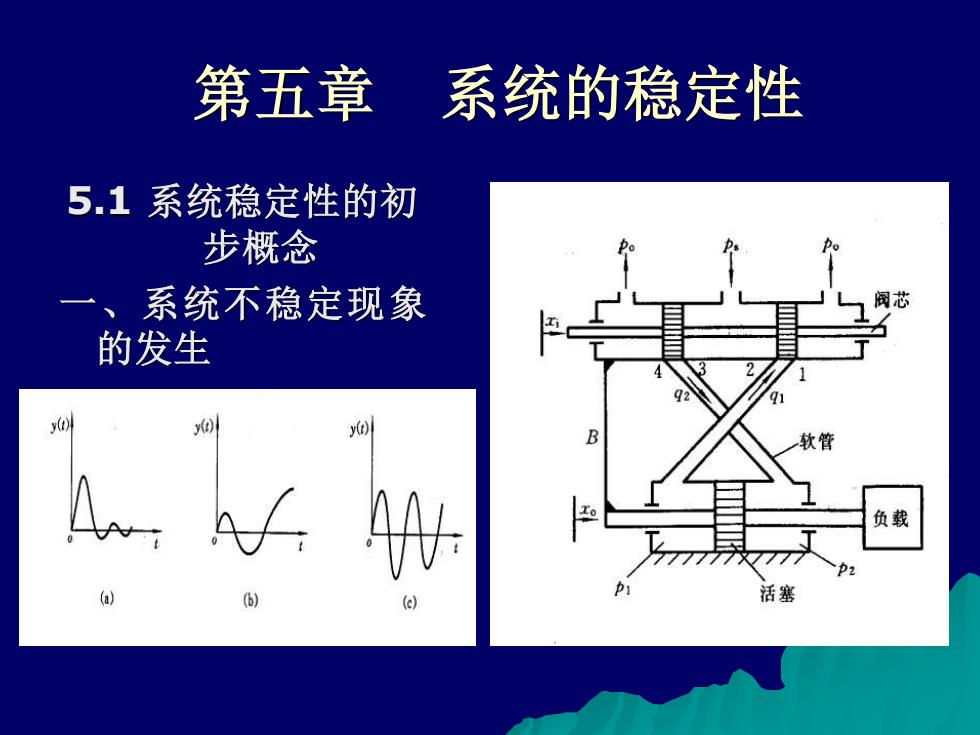
第五章 系统的稳定性 5.1系统稳定性的初 步概念 一、系统不稳定现象 的发生 y(r) B 负载 活塞
第五章 系统的稳定性 5.1 系统稳定性的初 步概念 一、系统不稳定现象 的发生


◆首先,线性系统不稳定现象发生与否,取 决于系统内部条件,而与输入无关。 ◆其次,系统发生不稳定现象必有适当的反 馈作用。 ◆第三,控制理论所讨论的稳定性其实都是 指自由振荡下的稳定性
◆首先,线性系统不稳定现象发生与否,取 决于系统内部条件,而与输入无关。 ◆其次,系统发生不稳定现象必有适当的反 馈作用。 ◆第三,控制理论所讨论的稳定性其实都是 指自由振荡下的稳定性

二、稳定的定义和条件 若系统在初始状态(不论是无输入时的初态,还是输 入引起的初态)的影响下,由它所引起的系统的时间 响应随着时间的推移,逐渐衰减并趋向于零,则该系 统为稳定的。 方法(1) 对于阶定常线性系统微分方程,拉氏变换后得到 X(s)= M X,(s)+ N(s) M(s) D(s) =G(s)为系统的传递函数 D(s) D(s) N(s)是与初始条件x(0)有关的s多项式,而x(0) 是输出x,(t)及其各阶导数x,)(t)在输入作用前t=0时刻 的值,即系统在输入前的初始状态
二、稳定的定义和条件 若系统在初始状态(不论是无输入时的初态,还是输 入引起的初态)的影响下,由它所引起的系统的时间 响应随着时间的推移,逐渐衰减并趋向于零,则该系 统为稳定的。 方法(1) 对于n阶定常线性系统微分方程,拉氏变换后得到 ( ) ( ) ( ) ( ) ( ) ( ) D s N s X s D s M s X s o = i + ( )为系统的传递函数 ( ) ( ) G s D s M s = 的值,即系统在输入前的初始状态。 是输出 及其各阶导数 在输入作用前 时刻 是与初始条件 有关的 多项式,而 ( ) ( ) 0 ( ) (0 ) s (0 ) ( ) ( ) ( ) = − − x t x t t N s x x k o o k o k o

稳定性就是研究初始状态下的输出情况。系统在初始 状态下的输出为 N(s) X(s)= D(s) 当特征方程的根各不相同时,系统的输出为 0=L'x,(s=t ]=∑Ae4 若系统的特征方程的根实部均为负值,即Re[si]<0, 则零输入响应最终将衰减为零。这样系统就是稳定的。 系统的输入项参数对系统稳定性没有影响,即传递函数 的零点对系统的稳定性无影响
稳定性就是研究初始状态下的输出情况。系统在初始 状态下的输出为 ( ) ( ) ( ) D s N s X s o = 当特征方程的根各不相同时,系统的输出为 s t n i o o i i A e D s N s x t L X s L = − − = = = 1 1 1 ] ( ) ( ) ( ) [ ( )] [ 若系统的特征方程的根实部均为负值,即Re[si]<0, 则零输入响应最终将衰减为零。这样系统就是稳定的。 系统的输入项参数对系统稳定性没有影响,即传递函数 的零点对系统的稳定性无影响