
二、稳定性判据 ■劳斯Routh)判据 系统稳定的充分必要条件是:劳斯表中第一列 所有元素的计算值均大于零。 若系统的特征方程为: os”+1S”+…+am-1S+n=0
二、稳定性判据 ◼ 劳斯(Routh)判据 系统稳定的充分必要条件是:劳斯表中第一列 所有元素的计算值均大于零。 1 0 1 0 + 1 + + − + = − n n n n a s a s a s a 若系统的特征方程为:
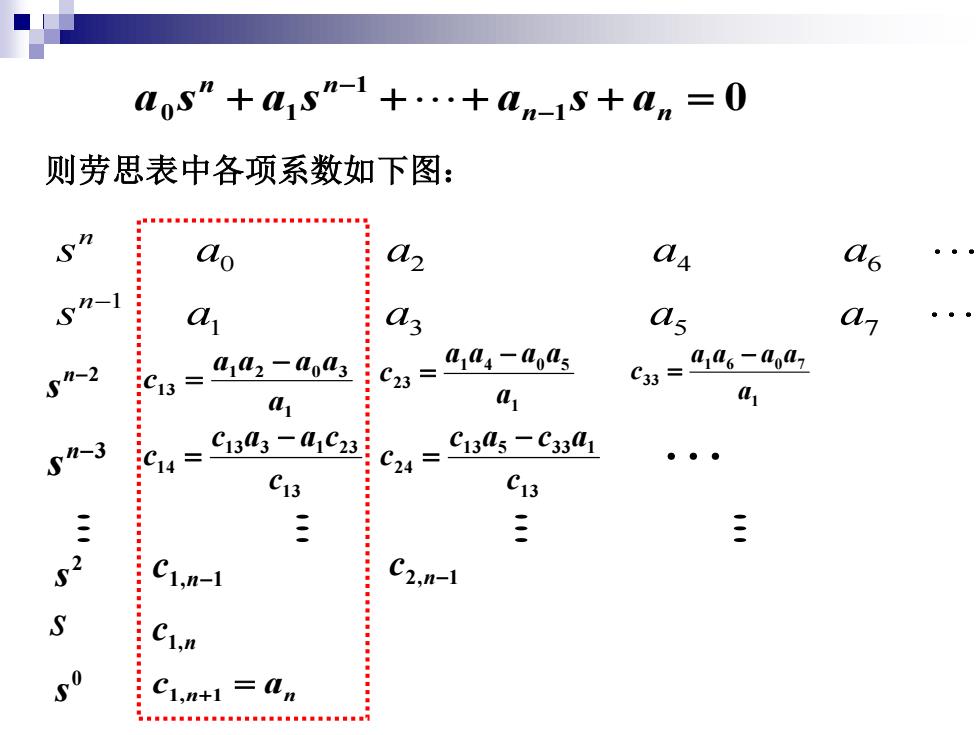
aos”+a1s-+…+an-1S+an=0 则劳思表中各项系数如下图: ao as : a : a3 as 2 1L2-4oL3 c23-44-04 C33= 106-7 41 L a S1-3 c4-94-0492 C24= C1345-C3341 C13 C13 CI,n-1 C2,n-1 C C1,n+1 an
则劳思表中各项系数如下图: 1 1 2 0 3 13 a a a a a c − n−2 = s 1 1 4 0 5 23 a a a a a c − = 1 1 6 0 7 33 a a a a a c − = n−3 s 13 13 3 1 23 14 c c a a c c − = 13 13 5 33 1 24 c c a c a c − = 2 s 1,n−1 c 2,n−1 c n c1, 0 s n an c1, +1 = 0 2 4 6 1 1 3 5 7 n n s a a a a s a a a a − s 1 0 1 0 + 1 + + − + = − n n n n a s a s a s a

关于劳斯判据的几点说明 如果第一列中出现一个小于零的值,系 统就不稳定; ■1 如果第一列中有等于零的值,说明系统 处于临界稳定状态; ■第一列中数据符号改变的次数等于系统 特征方程正实部根的数目,即系统中不 稳定根的个数
关于劳斯判据的几点说明 ◼ 如果第一列中出现一个小于零的值,系 统就不稳定; ◼ 如果第一列中有等于零的值,说明系统 处于临界稳定状态; ◼ 第一列中数据符号改变的次数等于系统 特征方程正实部根的数目,即系统中不 稳定根的个数

例1 设系统特征方程如下: s4+253+352+4s+5=0 试用劳斯判据判断该系统的稳定性,并确 定正实部根的数目
例1 设系统特征方程如下: 2 3 4 5 0 4 3 2 s + s + s + s + = 试用劳斯判据判断该系统的稳定性,并确 定正实部根的数目

解:特征方程 s4+2s3+3s2+45+5=0 3 5 2 4 0 2 2x3-1×4-1 2×5-1×0 2 2 5 1×4-2×5 -6 DE 5 结论:系统不稳定;系统特征方程有两个正实部的根
解:特征方程 4 s 1 3 5 3 s 2 4 0 2 s 2 2 3 −14 = 1 2 25 −10 = 5 0 1 s 1 14 − 25 = −6 0 0 s 5 + − − + 结论:系统不稳定;系统特征方程有两个正实部的根。 2 3 4 5 0 4 3 2 s + s + s + s + =