§4-3置换定理 定义:若网络N由两个单口网络N,和N2连接组成,且各 支路电压、电流均有惟一解。设已知端口电压和电流 值分别为o和邮,则N2(或N)可以用一个电压为的电 压源(图b)或用一个电流为β的电流源(图c)置换,不 影响N(或N2)内各支路电压、电流原有数值,只要 在置换后,网络仍有惟一解。 B N = N2 N 0 (a) (b) (c) 11
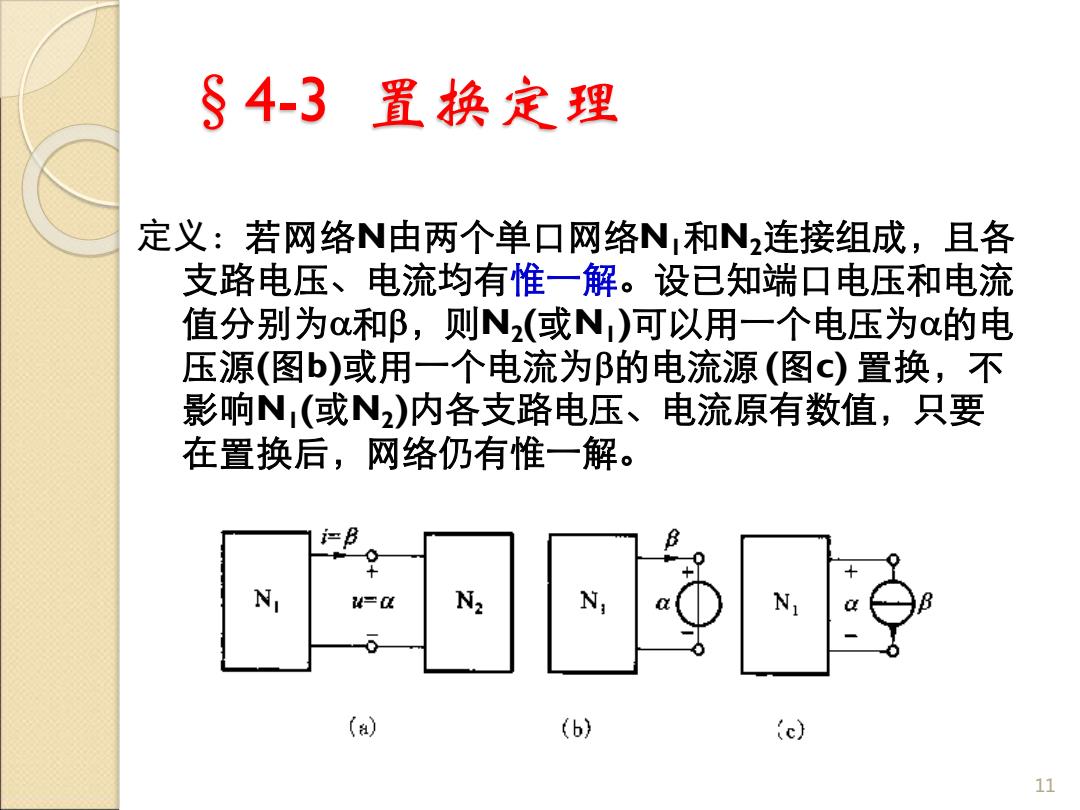
§4-3 置换定理 定义:若网络N由两个单口网络N1和N2连接组成,且各 支路电压、电流均有惟一解。设已知端口电压和电流 值分别为和,则N2 (或N1 )可以用一个电压为的电 压源(图b)或用一个电流为的电流源 (图c) 置换,不 影响N1 (或N2 )内各支路电压、电流原有数值,只要 在置换后,网络仍有惟一解。 11
证明 设在图(a)所示的网络中 根据两类约束关系已解 N2 出各支路的电压、电流。 (a) (b) 例如,N,内某支路k的 电压、电流分别为: ux =ak,ik Be (c) 端口电压、电流分别为:u=x,i=B 若N2用一个电压为0的电压源所置换,如图(b),需要 论证支路k电压、电流的解答山k'和k'仍应为: ux ax,in Br 端口电流'的解答则应为: i=B 12
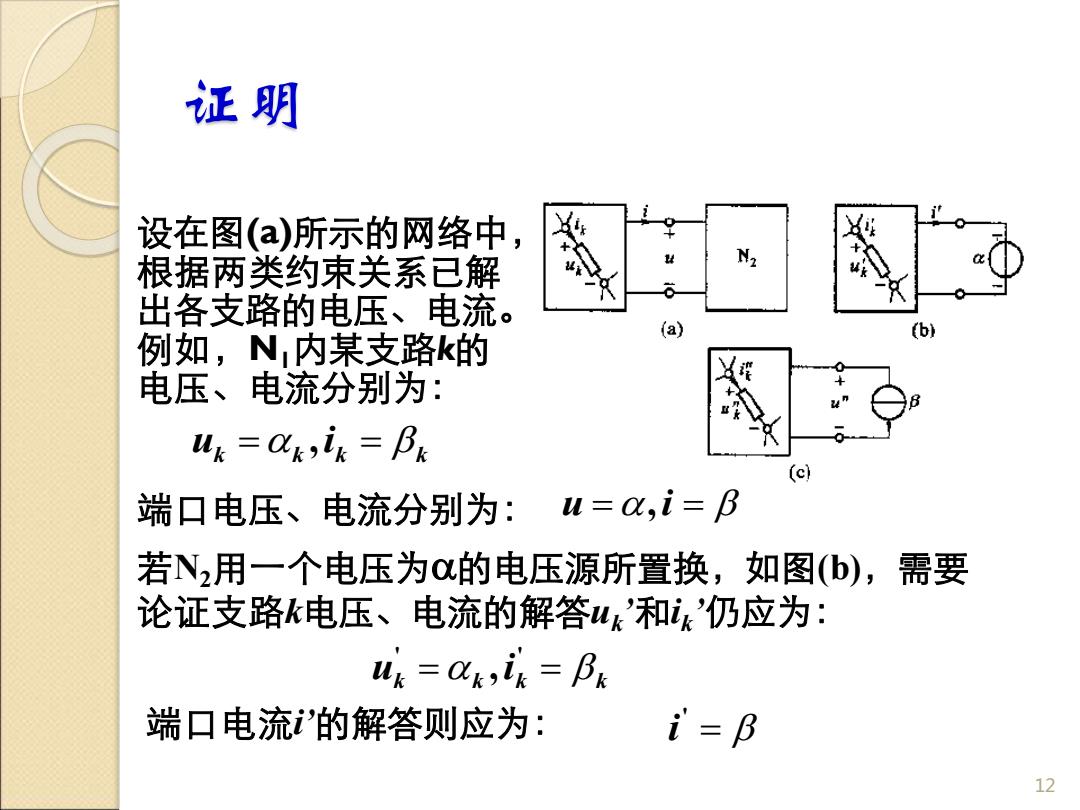
证明 设在图(a)所示的网络中, 根据两类约束关系已解 出各支路的电压、电流。 例如,N1内某支路k的 电压、电流分别为: 12 端口电压、电流分别为: 若N2用一个电压为的电压源所置换,如图(b),需要 论证支路k电压、电流的解答uk ’和ik ’仍应为: 端口电流i’的解答则应为: k k k k u = ,i = u =,i = k k k k u = i = ' ' , = ' i

证明(续) 冬对图(b),一个典型的KCL方程的形式为: ∑4=0 冬该方程系根据某一包含支路k的节点n写出的。如以假 定的解答ik=B代入,需要论证 ∑B=0 显然,这一式子是成立的,因为同样的节点n也存在 于图()的网络之中,而电流B正是该网络惟一的一组 解答。 13
证明(续) ❖ 对图(b),一个典型的KCL方程的形式为: ❖ 该方程系根据某一包含支路k的节点n写出的。如以假 定的解答ik ’=k代入,需要论证 ❖ 显然,这一式子是成立的,因为同样的节点n也存在 于图(a)的网络之中,而电流k正是该网络惟一的一组 解答。 13 0 ' i k = k = 0

证明(续) *也可论证所设的解答也满足KVL以及N内部所有元 件的VAR。 ÷剩下的工作是要论证所设的解答是否满足用以置换 N2的电压源的VAR。 ”回答也是肯定的,因为流过电压源的电流可以为任 何值。 14
证明(续) ❖ 也可论证所设的解答也满足KVL以及N1内部所有元 件的VAR。 ❖ 剩下的工作是要论证所设的解答是否满足用以置换 N2的电压源的VAR。 ❖ 回答也是肯定的,因为流过电压源的电流可以为任 何值。 14

证明(续) 对图(c)所示用电流为的电流源置换N2的情况,也可 用同样的方法论证: Lk=ak,ik=阝e 而端口电压 15
证明(续) ❖ 对图(c)所示用电流为的电流源置换N2的情况,也可 用同样的方法论证: 而端口电压 15 k k k k u = i = " " , = " u