置换定理的作用 利用置换定理,我们可以先求得N,和N2的端口电压 和端口电流,把原电路分为两个子网络,进而求出 N,及N2所有支路电压和电流。 Na N N2 (a) (b) (a} (b) 16
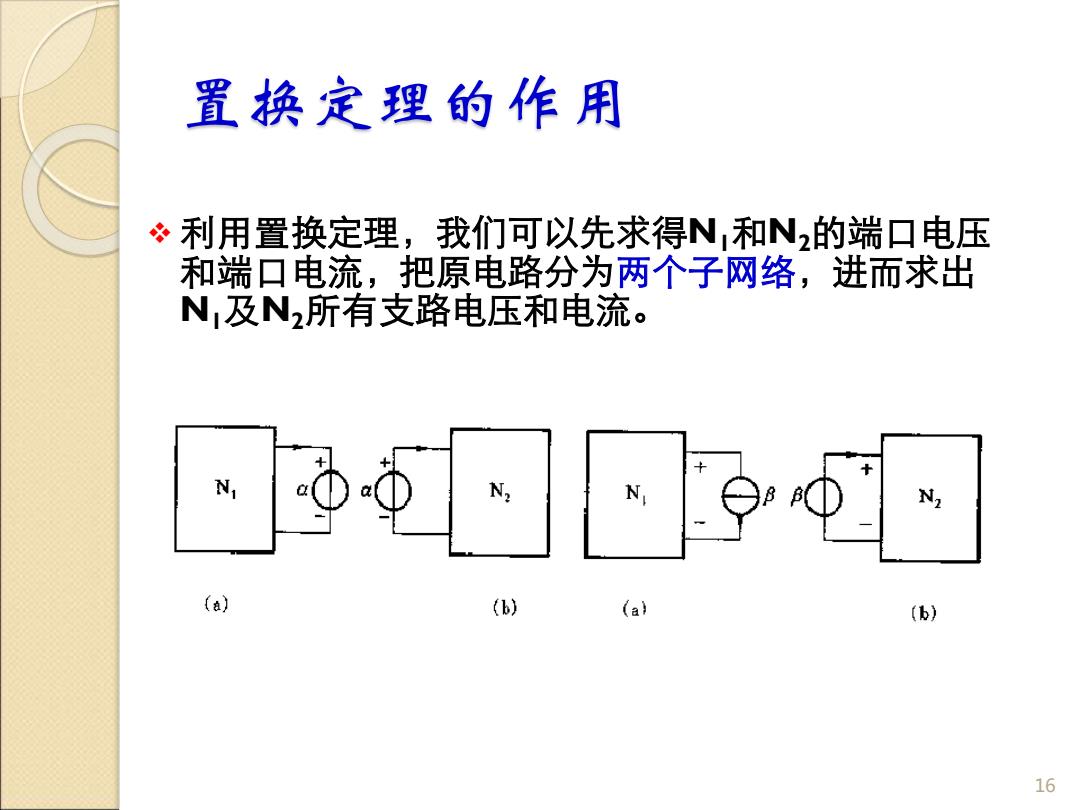
置换定理的作用 ❖ 利用置换定理,我们可以先求得N1和N2的端口电压 和端口电流,把原电路分为两个子网络,进而求出 N1及N2所有支路电压和电流。 16
倒 0.5i 试用分解方法求i,和u2。 62 102 解(1)自图中虚线处 把电路分为两个单口 R2 12v( 1A 网络N1和N2,端口电 5 压u和电流的参考方 N2 向如图。 (2)求N1和N2的VAR。N1的VAR为: u (i+is-ai)R,+(i+is)R +us +iRs [us+(R1+r2)is]+[R1+R3+(1-ax)R2]5 [12+(6+10)×1]+[6+5+(1-0.5)×10]5 = =28+16i 17
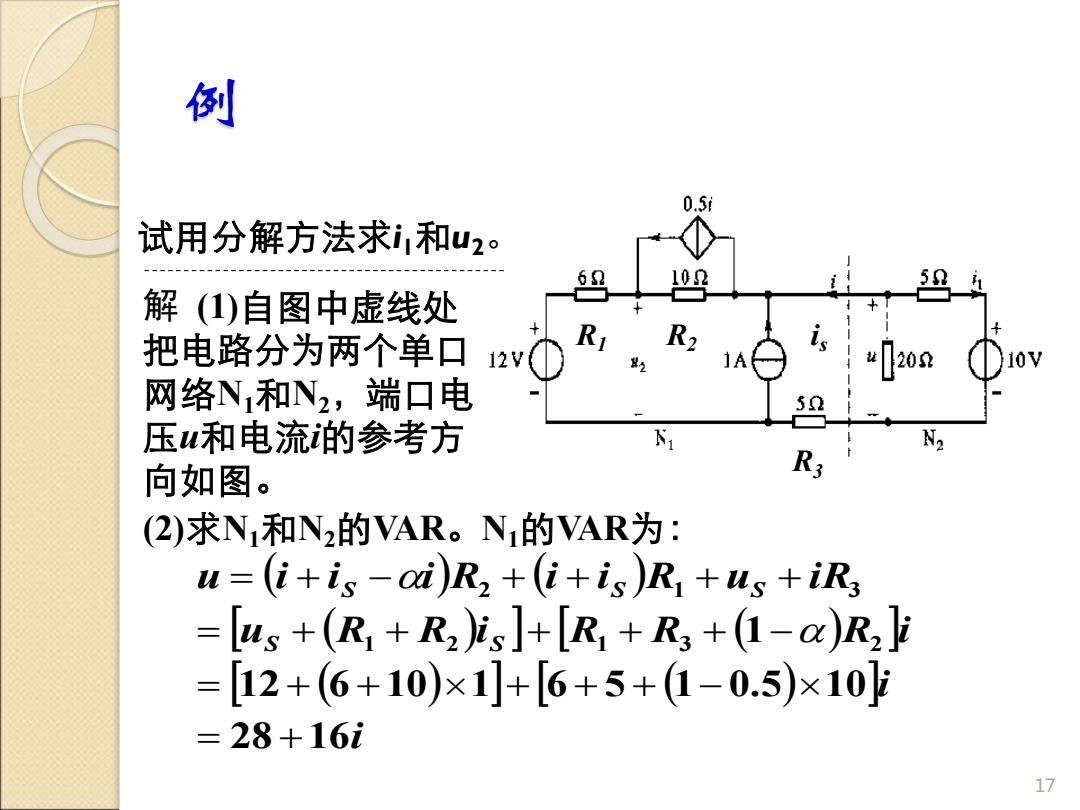
例 试用分解方法求i1和u2。 17 解 (1)自图中虚线处 把电路分为两个单口 网络N1和N2,端口电 压u和电流i的参考方 向如图。 (2)求N1和N2的VAR。N1的VAR为: i s ( ) ( ) ( ) ( ) ( ) ( ) i i u R R i R R R i u i i i R i i R u i R S S S S S 28 16 12 6 10 1 6 5 1 0.5 10 1 2 1 3 1 2 2 1 3 = + = + + + + + − = + + + + + − = + − + + + + R1 R2 R3
解答 N2的节点电压方程为: 0.5 g+0gx10= 12y u=8-4i (3)联立两者的VAR,解u,i。 N N2 8-4i=28+16i i=-1A u=12V 节点电流和为零 (4)以I2V电压源置换N1,可得: 12-1 w=5i+10 i= 5 0A=0.4 以-IA电流源置换N2,因62电阻上无电流,可得 u2=12V 18
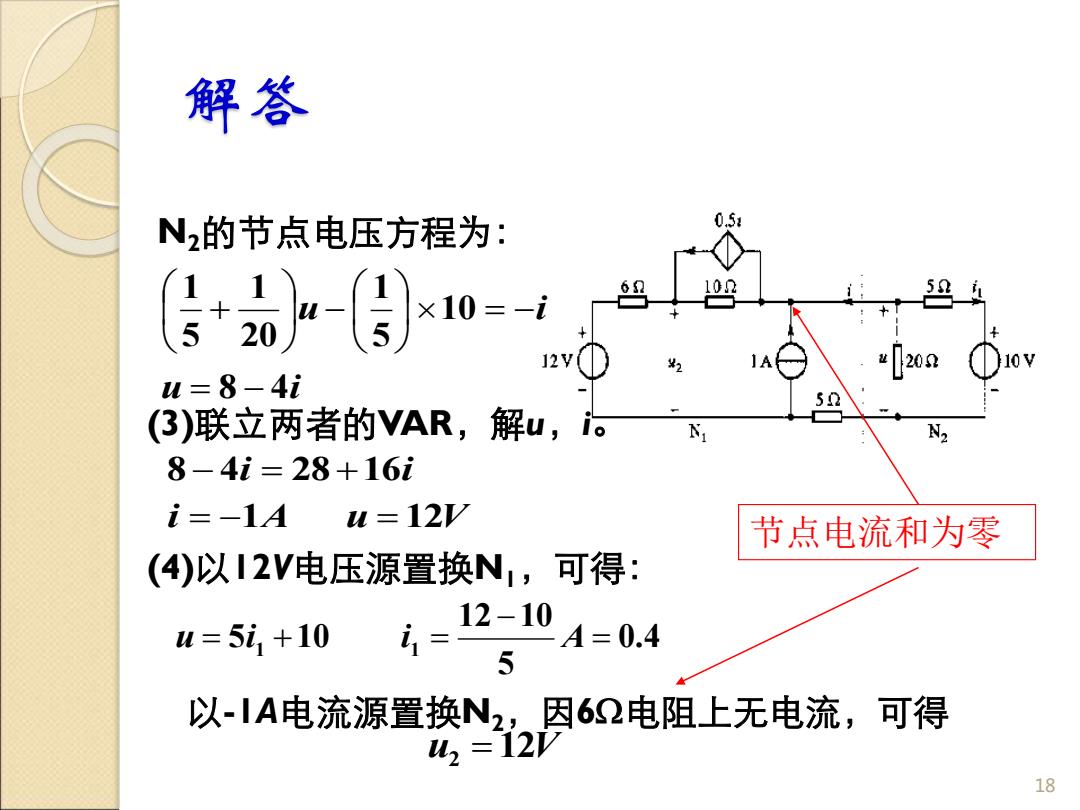
解答 N2的节点电压方程为: (3)联立两者的VAR,解u,i。 (4)以12V电压源置换N1,可得: 以-1A电流源置换N2,因6电阻上无电流,可得 18 节点电流和为零 u i u i 8 4 10 5 1 20 1 5 1 = − = − − + i A u V i i 1 12 8 4 28 16 = − = − = + 0.4 5 12 10 5 1 10 1 = − u = i + i = A u2 = 12V
倒 已知非线性电阻的伏安特性曲 线如图(b)所示,试求非线性电 阻两端的电压u和流过的电流。 解将线性部分与非线性部分划 () (b) 分为两个单口网络,用节点法 求得线性单口的VAR为 2u=Us-Ri UR =() 在非线性电阻VAR的同一个 -平面上作出线性部分的伏安 特性曲线,这是一条直线,两条 线的交点便是所求解答。 0 2 19
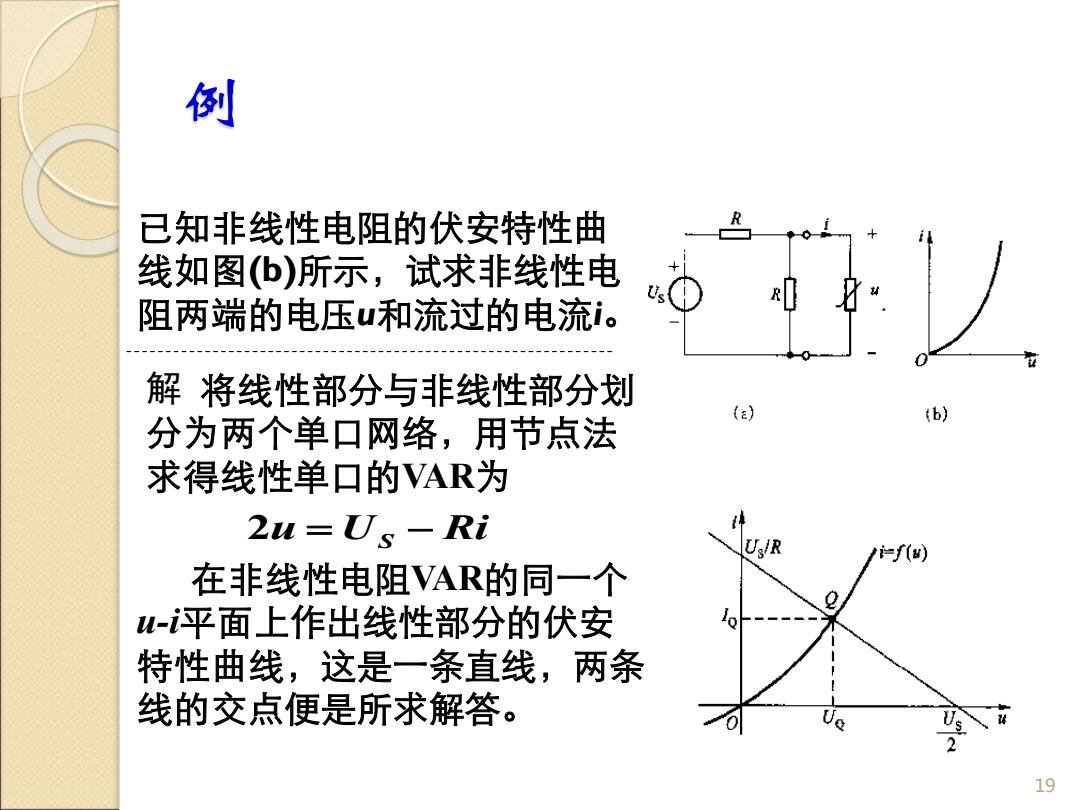
例 已知非线性电阻的伏安特性曲 线如图(b)所示,试求非线性电 阻两端的电压 u和流过的电流 i 。 19 解 将线性部分与非线性部分划 分为两个单口网络,用节点法 求得线性单口的VAR 为 在非线性电阻VAR的同一个 u - i平面上作出线性部分的伏安 特性曲线,这是一条直线,两条 线的交点便是所求解答。 u U Ri 2 = S −
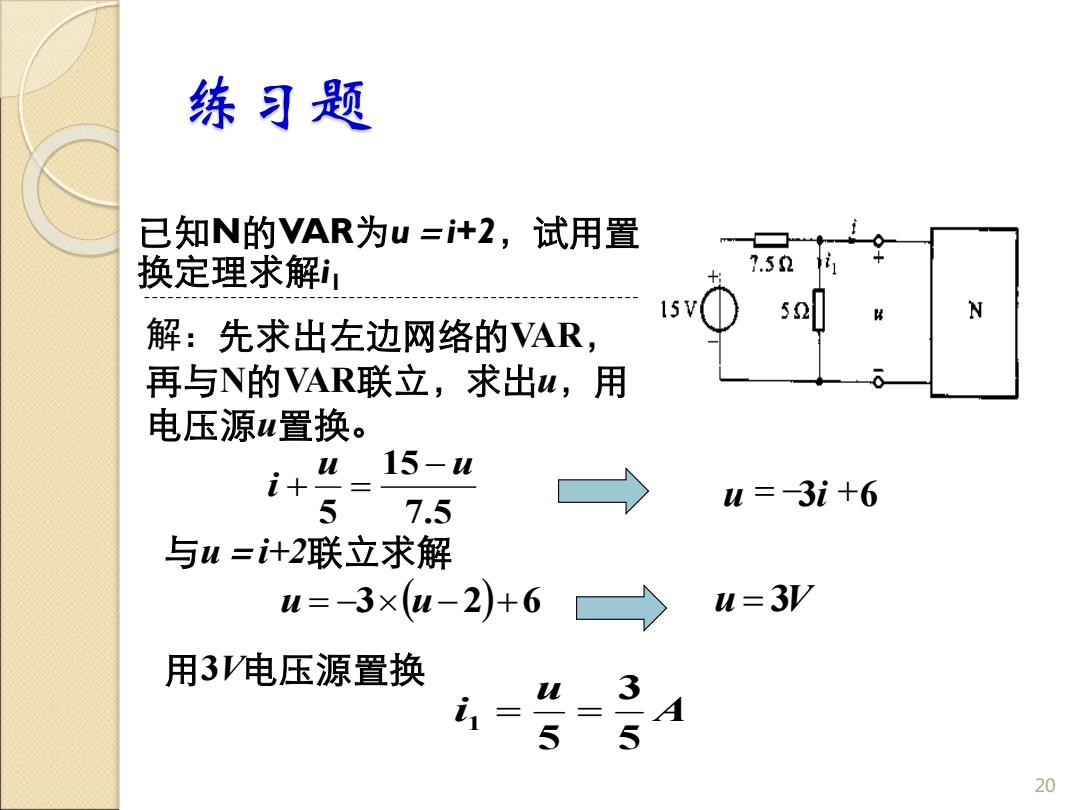
练习题 已知N的VAR为u=i+2,试用置 换定理求解, 7.5 15V N 解:先求出左边网络的VAR, 再与N的VAR联立,求出W,用 电压源u置换。 15-u u i+ 5 7.5 u=-3i+6 与u=+2联立求解 u=-3×(u-2)+6 u =3V 用3V电压源置换 = 5 3-5 A 20
练习题 已知N的VAR为u=i+2,试用置 换定理求解i1 20 7.5 15 5 u u i − + = 解:先求出左边网络的VAR, 再与N的VAR联立,求出u,用 电压源u置换。 与u=i+2联立求解 u = −3(u−2)+6 u = 3V 用3V电压源置换 A u i 5 3 5 1 = = u = −3i +6