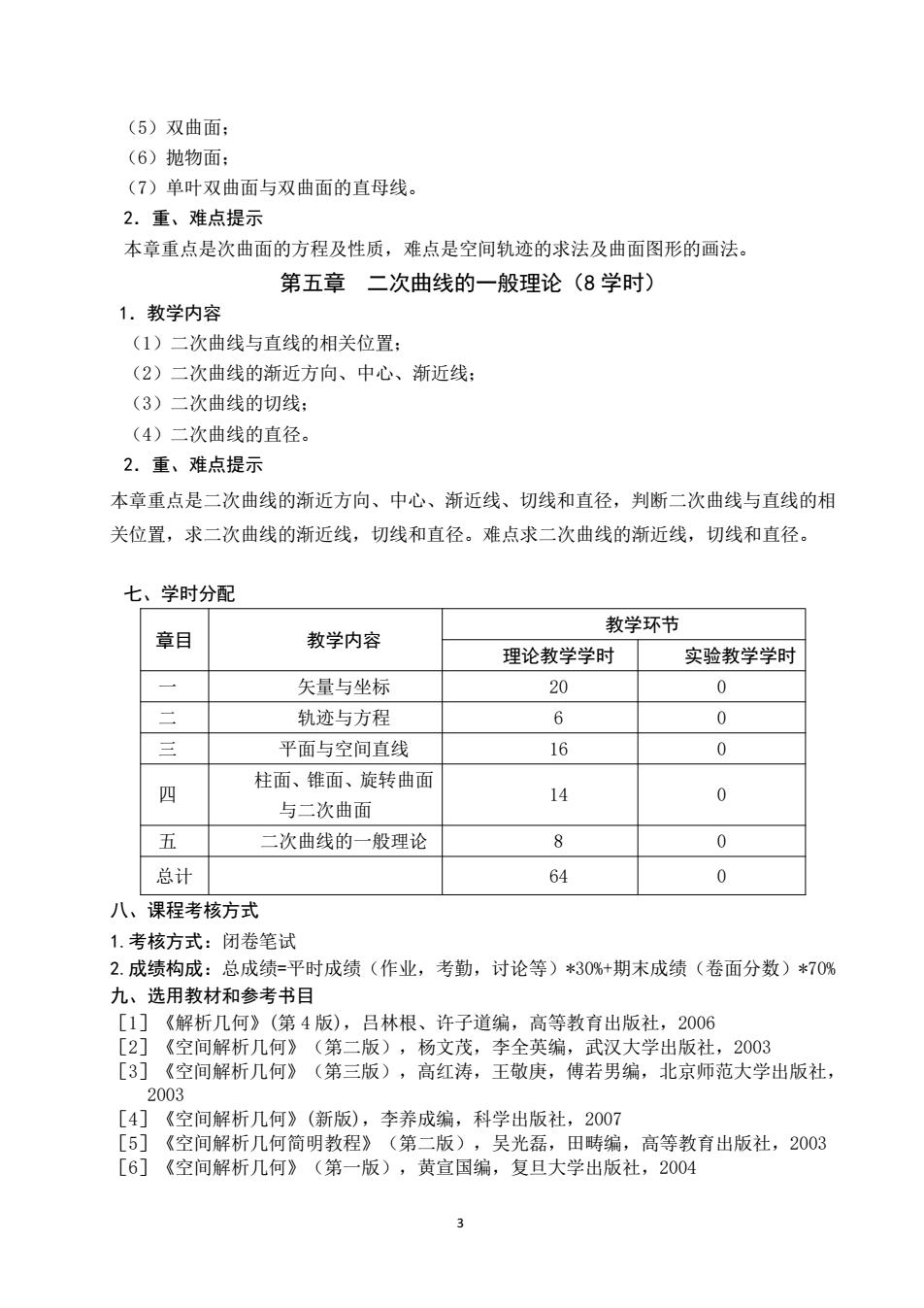
(5)双曲面: (6)抛物面: (7)单叶双曲面与双曲面的直母线。 2.重、难点提示 本章重点是次曲面的方程及性质,难点是空间轨迹的求法及曲面图形的画法。 第五章二次曲线的一般理论(8学时) 1.教学内容 (1)二次曲线与直线的相关位置: (2)二次曲线的渐近方向、中心、渐近线: (3)二次曲线的切线: (4)二次曲线的直径。 2.重、难点提示 本章重点是二次曲线的渐近方向、中心、渐近线、切线和直径,判断二次曲线与直线的相 关位置,求二次曲线的渐近线,切线和直径。难点求二次曲线的渐近线,切线和直径。 七、学时分配 教学环节 章目 教学内容 理论教学学时 实验教学学时 矢量与坐标 20 0 二 轨迹与方程 6 0 三 平面与空间直线 16 0 柱面、锥面、旋转曲面 四 14 0 与二次曲面 五 二次曲线的一般理论 8 0 总计 64 0 八、课程考核方式 1.考核方式:闭卷笔试 2.成绩构成:总成绩=平时成绩(作业,考勤,讨论等)30%+期末成绩(卷面分数)*70% 九、选用教材和参考书目 [1]《解析几何》(第4版),吕林根、许子道编,高等教育出版社,2006 [2]《空间解析几何》(第二版),杨文茂,李全英编,武汉大学出版社,2003 [3]《空间解析几何》(第三版),高红涛,王敬庚,傅若男编,北京师范大学出版社, 2003 [4]《空间解析几何》(新版),李养成编,科学出版社,2007 [5]《空间解析几何简明教程》(第二版),吴光磊,田畴编,高等教育出版社,2003 [6]《空间解析几何》(第一版),黄宣国编,复旦大学出版社,2004 3
3 (5)双曲面; (6)抛物面; (7)单叶双曲面与双曲面的直母线。 2.重、难点提示 本章重点是次曲面的方程及性质,难点是空间轨迹的求法及曲面图形的画法。 第五章 二次曲线的一般理论(8 学时) 1.教学内容 (1)二次曲线与直线的相关位置; (2)二次曲线的渐近方向、中心、渐近线; (3)二次曲线的切线; (4)二次曲线的直径。 2.重、难点提示 本章重点是二次曲线的渐近方向、中心、渐近线、切线和直径,判断二次曲线与直线的相 关位置,求二次曲线的渐近线,切线和直径。难点求二次曲线的渐近线,切线和直径。 七、学时分配 章目 教学内容 教学环节 理论教学学时 实验教学学时 一 矢量与坐标 20 0 二 轨迹与方程 6 0 三 平面与空间直线 16 0 四 柱面、锥面、旋转曲面 与二次曲面 14 0 五 二次曲线的一般理论 8 0 总计 64 0 八、课程考核方式 1.考核方式:闭卷笔试 2.成绩构成:总成绩=平时成绩(作业,考勤,讨论等)*30%+期末成绩(卷面分数)*70% 九、选用教材和参考书目 [1]《解析几何》(第 4 版),吕林根、许子道编,高等教育出版社,2006 [2]《空间解析几何》(第二版),杨文茂,李全英编,武汉大学出版社,2003 [3]《空间解析几何》(第三版),高红涛,王敬庚,傅若男编,北京师范大学出版社, 2003 [4]《空间解析几何》(新版),李养成编,科学出版社,2007 [5]《空间解析几何简明教程》(第二版),吴光磊,田畴编,高等教育出版社,2003 [6]《空间解析几何》(第一版),黄宣国编,复旦大学出版社,2004

《数学分析》课程教学大纲 课程名称:数学分析 课程类别:专业基础课 适用专业:信息与计算科学 考核方式:考试 总学时、学分:288学时18学分 其中实验学时:Q学时 一、课程教学目的 数学分析是信息与计算科学专业一门必修专业基础课。本课程的目的是通过系统的学 习与严格的训练,使学生对极限思想和方法有较深入的认识,对具体和抽象、特殊与一般、 有限与无限等辩证关系有一定得了解,全面掌握数学分析的基本理论知识:培养严格的逻 辑思维能力与推理论证能力:具备熟练的运算能力与技巧:提高建立数学模型,并应用微 积分这一工具解决实际应用问题的能力。 二、课程教学要求 本课程教学要求学生切实掌握数学分析中的基本概念、基本理论和基本方法,对知识 内容融会贯通。同时,通过典型例题的分析,讲解,使学生学会分析问题、解决问题、独 立思考,及时保质保量完成课后习题。 三、先修课程 无 四、课程教学重、难点 教学重点:有极限理论、一元(多元)微积分学,级数理论。 教学难点:有一元函数一致连续性、广义积分敛散性判定、实数完备性、函数项级数 一致收敛性、含参量积分一致收敛性的判定及其和函数的解析性质的讨论。 五、课程教学方法与教学手段 数学分析教学采用“二合一”教学模式。二合一教学模式是指:传统黑板教学+多媒 体辅助教学。 六、课程教学内容 第一章 实数集与函数(8学时) 1.教学内容 (1)实数: (2)函数概念: (3)具有某些特性的函数。 2.重、难点提示 (1)重点是实数集、确界、函数的概念及其有关性质: (2)难点是确界的定义及其应用。 4
4 《数学分析》课程教学大纲 课程名称:数学分析 课程类别:专业基础课 适用专业:信息与计算科学 考核方式:考试 总学时、学分:288 学时 18 学分 其中实验学时:0 学时 一、课程教学目的 数学分析是信息与计算科学专业一门必修专业基础课。本课程的目的是通过系统的学 习与严格的训练,使学生对极限思想和方法有较深入的认识,对具体和抽象、特殊与一般、 有限与无限等辩证关系有一定得了解,全面掌握数学分析的基本理论知识;培养严格的逻 辑思维能力与推理论证能力;具备熟练的运算能力与技巧;提高建立数学模型,并应用微 积分这一工具解决实际应用问题的能力。 二、课程教学要求 本课程教学要求学生切实掌握数学分析中的基本概念、基本理论和基本方法,对知识 内容融会贯通。同时,通过典型例题的分析,讲解,使学生学会分析问题、解决问题、独 立思考,及时保质保量完成课后习题。 三、先修课程 无 四、课程教学重、难点 教学重点:有极限理论、一元(多元)微积分学,级数理论。 教学难点:有一元函数一致连续性、广义积分敛散性判定、实数完备性、函数项级数 一致收敛性、含参量积分一致收敛性的判定及其和函数的解析性质的讨论。 五、课程教学方法与教学手段 数学分析教学采用“二合一”教学模式。二合一教学模式是指:传统黑板教学+多媒 体辅助教学。 六、课程教学内容 第一章 实数集与函数(8 学时) 1.教学内容 (1)实数; (2)函数概念; (3)具有某些特性的函数。 2.重、难点提示 (1)重点是实数集、确界、函数的概念及其有关性质; (2)难点是确界的定义及其应用

第二章数列极限(14学时) 1.教学内容 (1)数列极限概念: (2)收敛数列的性质; (3)数列极限存在的条件。 2.重、难点提示 (1)重点是数列极限的概念、收敛数列的性质及计算极限: (2)难点是数列极限的“E-N”定义及其应用。 第三章函数极限(14学时) 1.教学内容 (1)函数极限概念: (2)函数极限的性质; (3)函数极限存在的条件: (4)两个重要的极限: (5)无穷小量与无穷大量。 2.重、难点提示 (1)重点是函数极限的概念,性质及其计算; (2)难点是柯西准则和海涅定理的运用。 第四章函数的连续性(14学时) 1.教学内容 (1)连续性概念: (2)连续函数的性质: (3)初等函数的连续性。 2.重、难点提示 (1)重点是函数连续性的概念和区间上连续函数的性质; (2)难点是一致连续性的概念及证明问题。 第五章导数和微分(12学时) 1.教学内容 (1)导数概念: (2)求导法则: (3)参变量函数的导数: (4)高阶导数: (5)微分。 5
5 第二章 数列极限(14 学时) 1.教学内容 (1) 数列极限概念; (2) 收敛数列的性质; (3) 数列极限存在的条件。 2.重、难点提示 (1) 重点是数列极限的概念、收敛数列的性质及计算极限; (2) 难点是数列极限的“ -N”定义及其应用。 第三章 函数极限(14 学时) 1.教学内容 (1) 函数极限概念; (2) 函数极限的性质; (3) 函数极限存在的条件; (4) 两个重要的极限; (5) 无穷小量与无穷大量。 2.重、难点提示 (1) 重点是函数极限的概念,性质及其计算; (2) 难点是柯西准则和海涅定理的运用。 第四章 函数的连续性(14 学时) 1.教学内容 (1) 连续性概念 ; (2) 连续函数的性质; (3) 初等函数的连续性。 2.重、难点提示 (1) 重点是函数连续性的概念和区间上连续函数的性质; (2) 难点是一致连续性的概念及证明问题。 第五章 导数和微分(12 学时) 1.教学内容 (1)导数概念; (2)求导法则; (3)参变量函数的导数; (4)高阶导数; (5)微分

2.重、难点提示 (1)重点是导数与微分的概念及其计算: (2)难点是求复合函数的导数。 第六章微分中值定理及其应用(18学时) 1.教学内容 (1)拉格朗日中值定理和函数的单调性: (2)柯西中值定理和不定式极限: (3)泰勒公式: (4)函数的极值与最大(小)值: (5)曲线的凸性与拐点: (6)函数图象的讨论。 2.重、难点提示 (1)重点是中值定理和泰勒公式,利用导数研究函数的单调性、极值与凸性: (2)难点是用辅助函数解决问题的方法。 第七章实数的完备性(8学时) 1.教学内容 (1)关于实数集完备性的基本定理: (2)上极限和下极限(了解)。 2.重、难点提示 本章重点及难点是实数完备性基本定理的证明和应用。 第八章不定积分(14学时) 1.教学内容 (1)不定积分的概念与基本积分公式: (2)换元积分法与分部积分法: (3)有理函数和可化为有理函数的不定积分。 2.重、难点提示 (1)重点是不定积分的基本概念与计算: (2)难点是不定积分的换元积分法与分部积分法。 第九章定积分(18学时) 1.教学内容 (1)定积分的概念: (2)牛顿一一莱布尼兹公式: (3)可积条件;定积分的性质: 6
6 2.重、难点提示 (1)重点是导数与微分的概念及其计算; (2)难点是求复合函数的导数。 第六章 微分中值定理及其应用(18 学时) 1.教学内容 (1)拉格朗日中值定理和函数的单调性; (2)柯西中值定理和不定式极限; (3)泰勒公式; (4)函数的极值与最大(小)值; (5)曲线的凸性与拐点; (6)函数图象的讨论。 2.重、难点提示 (1)重点是中值定理和泰勒公式,利用导数研究函数的单调性、极值与凸性; (2)难点是用辅助函数解决问题的方法。 第七章 实数的完备性(8 学时) 1.教学内容 (1)关于实数集完备性的基本定理; (2)上极限和下极限(了解)。 2.重、难点提示 本章重点及难点是实数完备性基本定理的证明和应用。 第八章 不定积分(14 学时) 1.教学内容 (1)不定积分的概念与基本积分公式; (2)换元积分法与分部积分法; (3)有理函数和可化为有理函数的不定积分。 2.重、难点提示 (1)重点是不定积分的基本概念与计算; (2)难点是不定积分的换元积分法与分部积分法。 第九章 定积分(18 学时) 1.教学内容 (1)定积分的概念; (2)牛顿——莱布尼兹公式; (3)可积条件;定积分的性质;

(4)微积分学基本定理; (5)定积分计算(续)。 2.重、难点提示 (1)重点是定积分的基本概念、性质、微积分学基本定理以及牛顿一莱布尼兹公式: (2)难点是可积条件。 第十章定积分的应用(8学时) 1.教学内容 (1)平面图形的面积: (2)由平行截面面积求体积: (3)平面曲线的弧长与曲率; (4)旋转曲面的面积: (5)定积分在物理上的某些应用。 2.重、难点提示 (1)重点是面积、弧长的计算: (2)难点是微元法的理解和应用。 第十一章反常积分(14学时) 1.教学内容 (1)反常积分概念: (2)无穷积分的性质与收敛判别: (3)瑕积分的性质与收敛判别法。 2.重、难点提示 (1)重点是反常积分的含义与性质,无穷积分收敛判别: (2)难点是非正常积分敛散性的判别。 第十二章数项级数(14学时) 1.教学内容 (1)级数的收敛性: (2)正项级数: (3)一般项级数。 2.重、难点提示 (1)重点是级数的基本概念与性质,正项级数敛散性的判别: (2)难点是一般项级数敛散性的判别法。 第十三章函数列和函数项级数(16学时) 1.教学内容 7
7 (4)微积分学基本定理; (5)定积分计算(续)。 2.重、难点提示 (1)重点是定积分的基本概念、性质、微积分学基本定理以及牛顿—莱布尼兹公式; (2)难点是可积条件。 第十章 定积分的应用(8 学时) 1.教学内容 (1)平面图形的面积; (2)由平行截面面积求体积; (3)平面曲线的弧长与曲率; (4)旋转曲面的面积; (5)定积分在物理上的某些应用。 2.重、难点提示 (1)重点是面积、弧长的计算; (2)难点是微元法的理解和应用。 第十一章 反常积分(14 学时) 1.教学内容 (1)反常积分概念; (2)无穷积分的性质与收敛判别; (3)瑕积分的性质与收敛判别法。 2.重、难点提示 (1)重点是反常积分的含义与性质, 无穷积分收敛判别; (2)难点是非正常积分敛散性的判别。 第十二章 数项级数(14 学时) 1.教学内容 (1)级数的收敛性; (2)正项级数; (3) 一般项级数。 2.重、难点提示 (1)重点是级数的基本概念与性质,正项级数敛散性的判别; (2)难点是一般项级数敛散性的判别法。 第十三章 函数列和函数项级数(16 学时) 1.教学内容