
3.1动态元件 、电容 电容VAR的积分形式: 4)= ·t时刻电压,记载了此时刻前电流作用的结果,故电容为记忆元件 研究实际电路时,总是从某一时刻开始的。设t=t为初始观察时刻: ,t?t0 式中 电容电压在to时刻的初始值(initial value),或初始状态(initial state),一般取to=0; 尽管电容是记忆元件,但不必研究t。时刻之前的电流作用,因为其 作用结果可由u(to)表示 6
一、 电容 6 3.1动态元件 研究实际电路时,总是从某一时刻开始的。设t=t0为初始观察时刻: • 电容电压在t0时刻的初始值(initial value),或初始状态(initial state),一般取t0 = 0 ; • 尽管电容是记忆元件,但不必研究t0时刻之前的电流作用,因为其 作用结果可由u(t0)表示 式中 1 ( ) ( ) t u t i d C x x - ? = ò 0 0 0 0 0 1 1 ( ) ( 1 ( ) ( ) ( ) , ) t t t t t u t i d i d t t C i d u t C C x x x x x x - ? = + = + ? ò ò ò 0 0 1 ( ) ( ) t u t i d C x x - ? = ò • t时刻电压,记载了此时刻前电流作用的结果,故电容为记忆元件

3.1动态元件 一、电容 若电容电压、电流的参考方向非关联: i()=.c du dt n0)=·蝌6k=*小-6收,1? 1、o
一、 电容 7 3.1动态元件 若电容电压、电流的参考方向非关联: u i C ( ) du i t C dt = - 0 0 0 ) + ( ) 1 1 ( ( ) ( ) , t t t u t i d i d t t t C u C x x x x - ? = - = - ? 蝌 0 0 1 ( )= ( )d t u t i C x x - ? - ò

3.1动态元件 、电容 3、电容的功率与储能 电容吸收的瞬时功率为(关联参考方向):p1)=0=Cu02 电容是储能元件,它不消耗能量,无源元件。 ●当p(①)>0时,说明电容是在吸收能量,处于充电状态 ●当p()<0时,说明电容是在释放能量,处于放电状态。 电容的储能为: wc)=蝌px= u(1) Cu(x)du(x) u(?) c)- = u(-∞)=0。电容在时刻t的储能: wc()= c20 2 电容在某一时刻t的储能仅取决于此时刻的电压,且储能≥0。 8
一、 电容 8 3.1 动态元件 电容吸收的瞬时功率为(关联参考方向): 3、电容的功率与储能 电容是储能元件,它不消耗能量,无源元件。 ⚫ 当 p(t) > 0时,说明电容是在吸收能量,处于充电状态; ⚫ 当 p(t) < 0时,说明电容是在释放能量,处于放电状态。 u(-∞) =0。电容在时刻 t 的储能: 电容在某一时刻 t 的储能仅取决于此时刻的电压,且储能 ≥0。 ( ) ( ) ( ) ( ) ( ) du t p t u t i t Cu t dt = = ( ) ( 2 ? ) 2 ( ) ( ) ( ) ( ) 1 1 ( ) ( ) 2 2 t u t C u w t p d Cu du Cu t C u x x x x - ? ? = = = = - - ? 蝌 14442 4443 1 2 ( ) ( ) 2 w t Cu t C = 电容的储能为:
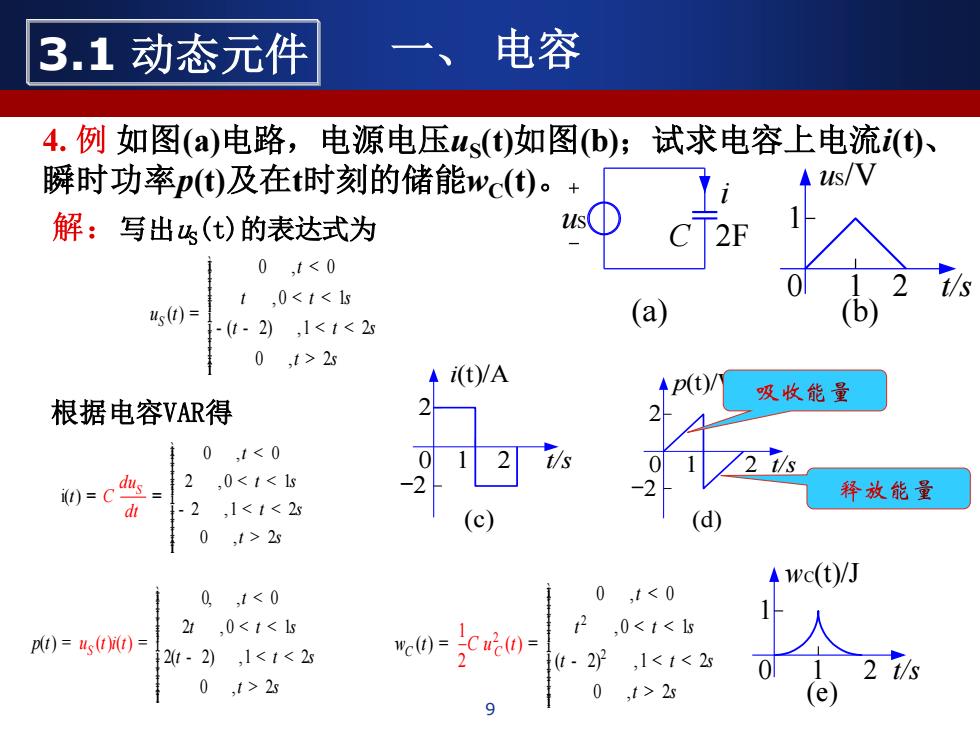
3.1动态元件 电容 4.例如图(a)电路,电源电压us(t)如图b);试求电容上电流()、 瞬时功率p)及在t时刻的储能wc()。+ us/V 解:写出5(t)的表达式为 21 0,t<0 t,0<t<1s 4s(t)= a -(t-2),1<1<2s 0,1>2s 本i(t)/A p(t)/ 吸收能量 根据电容VAR得 0 ,1<0 2 t/s dus .0<t<Is 0=c -2 释放能量 d .2 ,1<1<2s (c) (d) 0,1>25 wc(t)/J 0,1<0 0,t<0 21,0<t<s 2,0<t< p)=))= 2t-2),1<1<2 1t.22 ,1<t<2s 0 2认 0,1>2s 0,t>2s e
一、 电容 9 3.1 动态元件 如图(a)电路,电源电压uS (t)如图(b);试求电容上电流i(t)、 瞬时功率p(t)及在t时刻的储能wC(t)。 uS C 2F i (a) uS/V 0 t/s 1 1 2 (b) 写出uS(t)的表达式为 根据电容VAR得 i(t)/A 0 t/s 2 1 2 (c) -2 p(t)/W 0 t/s 2 1 2 (d) -2 wC(t)/J 0 t/s 1 1 2 (e) 0 , 0 , 0 1 ( ) ( 2) ,1 2 0 , 2 S t t t s u t t t s t s ìï < < < = í ï - - < < > î 0 , 0 2 , 0 1 i( ) 2 ,1 2 0 , 2 S t t s t t s u t s d C dt ìï < < < = = í ï - < < > î 0, , 0 2 , 0 1 ( ) 2( 2) ,1 2 ( 2 ( 0 ) ) , S t t t s p t t t s t s u t i t ìï < < < = = í ï - < < > î 2 2 2 0 , 0 , 0 1 ( ) ( , 1 ( 2) 1 0 ) 2 2 , 2 C C t t t s w t t t s t s C u t ìï < < < = = í ï - < < > î