《结构力学》课程教学资源（PPT课件讲稿）第6章 结构位移计算与虚功——能量法简述

6-2 变形体虚功原理的应用 例 Fp Mp Fprsin Mp=rsin For=F cos0 Fo=cos0 、0 FNp Fp sine F=sin 解 4=0,5mo,上n9a EI GA EA sinsin 之)rd0 El GA EA For Fr GA EA

6-2 变形体虚功原理的应用 FP r FQP FNP MP θ P P QP P NP P P Q N sin cos s s in cos in sin M F r M F F F r F F F             2 2 2 2 P P P 0 sin cos sin ( )d s BV F r kF F s EI GA EA         2 2 2 2 2 P P P 0 3 P P P sin cos sin ( ) d 4 F r kF F r EI GA EA F r F r F r k EI GA EA                    FP r r B 例 解

6-2 变形体虚功原理的应用 讨论 对于矩形截面(bXh) k=1.2 A=121 let G=0.4E then 与弯曲变形相比，剪切和轴向变 形对位移的影响，可以忽略不计

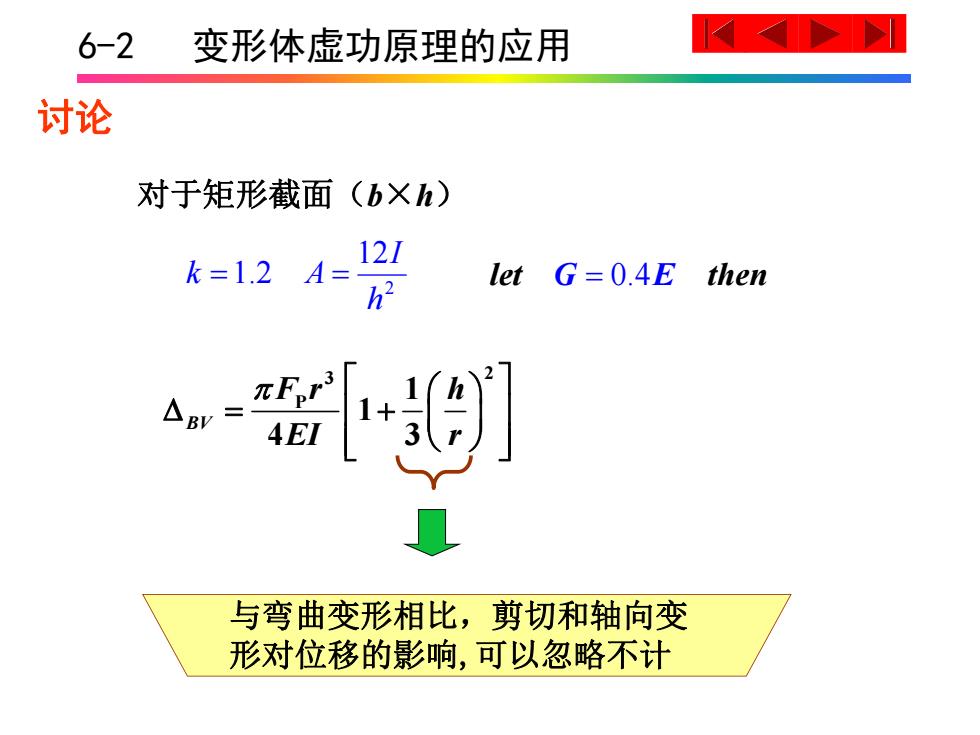
6-2 变形体虚功原理的应用 2 12 1.2 h I k  A  对于矩形截面（b×h） let G  0.4E then 2 3 P 1 1 4 3 BV F r h EI r                 与弯曲变形相比，剪切和轴向变 形对位移的影响,可以忽略不计 讨论

6-2 变形体虚功原理的应用 各类结构的计算公式简化 ■刚架、梁：只考虑弯曲变形引起的位移 EI ■对于桁架：只有轴力 a-5G4=y NFNP! EA ■对于拱：通常只有弯曲一项。当拱轴与压力曲线相近 时，需考虑弯曲和轴向变形两项。 A-dx+ Medx EA El

6-2 变形体虚功原理的应用 ■刚架、梁：只考虑弯曲变形引起的位移 d P l MM x EI    ■对于桁架：只有轴力 N NP N NP d l F F F F l x EA EA     ■对于拱：通常只有弯曲一项。当拱轴与压力曲线相近 时，需考虑弯曲和轴向变形两项。 N NP P d d l F F MM x x EA EI      各类结构的计算公式简化

6-2 变形体虚功原理的应用 【例】已知：各杆EA相同，求：△CH△c B 1 B B Fp FN2 【解】 d=+2a EA EA

6-2 变形体虚功原理的应用   P CH F a EA      P   1 2 2 CV F a EA     已知：各杆EA相同，求： CH、 CV FP a a A B C D FNP P  2F FP FP FN1 1 A B C D 1 FN2  2 1 【例】 【解】 A B C D 1

6-2 变形体虚功原理的应用 例杆件E=常数。试求△、B 1 解4，=290-)八a,=1-x M2=-1 y Ar=a,7dr =3- 1 X 914 )1 0,=立防0-)d 914 6EI ()

6-2 变形体虚功原理的应用   2 P 1 2 1 1 2 M  q l  x M  l  x M   例 杆件EI=常数。试求 AV、 A 解       P 0 2 0 4 1 d 1 1 d 2 8 l AV l M M x EI q l x l x x EI ql EI              q l A x 1 1       2 0 4 1 1 1 d 2 6 l A q l x x EI ql EI         