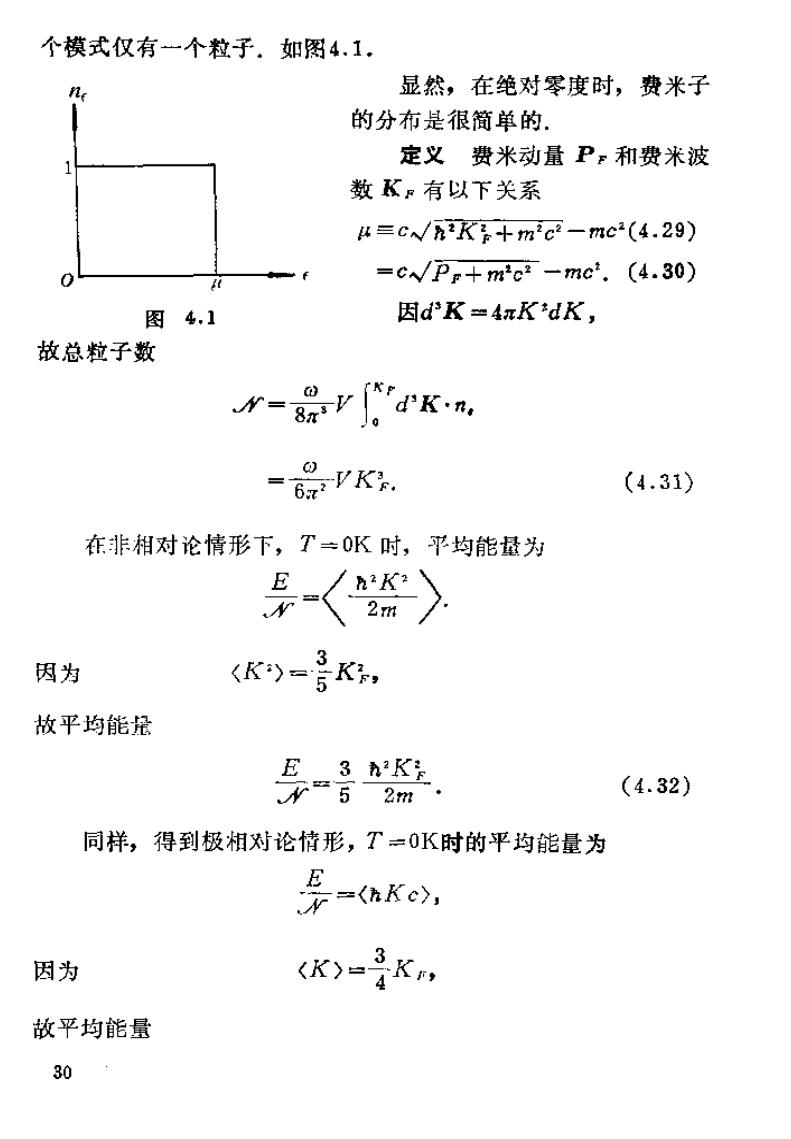
个模式仅有一个粒子.如图4.1. 显然,在绝对零度时,费米子 的分布是很简单的 定义费米动量P。和费米波 数Kr有以下关系 4三c/n2K+h2c2-mc2(4.29) =cWPr+m2o2-mc.(4.30) 图4.1 因dK=4πKdK, 故总粒子数 ΨK. 0 (4.31》 在非相对论情形下,T=0K时,平均能量为 因为 K)-号K, 故平均能捻 E 3 hKi 52m (4.32) 同样,得到极相对论情形,T=0K时的平均能量为 E =(hKc), 因为 K)-K 故平均能量 30

E=3 Kec. (4.33) 如将压强和能量的关系式(4.27)和(4.28)式表示为压强和密 度的关系,可得到两个重要的结论:在非相对论情形下 (4.34) 在极相对论情形下 (4.35) 现利用这些理论公式做一些物理的应用运算】 例1白矮星. 在宇宙中,白矮星是很多的,测量得较准的是天狼星B.它 的质量相当于太阳的质量M©,半径却比太阳的小100倍,和地球 的半径相当.于是在白矮星内的原子半径就是10-1厘米,也·了 势必被挤出来,形成简并的费米气状态。可以计算,白矮尾内部 受到由引力所造成的压力是很大的.是什么力量支撑不致下垮 呢?这需要做一数量级的估计,为方便计,我们忽略了常数π以 GM 及10以下的数字.于是白矮星内的吸引力是产(R是白矮星的 半径),如果是电子气向外膨胀与之相抗衡,则有 GM2 Ri~PR, (4.36) p为电子气的压强。如果白矮星的质量不很大,其内部的电子受 到引力的压缩仅达到非相对论情形.在此情形下,压强与密度呈 3次方的关系,所以 (0)R, 31

即 R~M-. (4.37) (4.37)式是半径与质量的 R 关系,它可以粗略地表示成图 4.2. R~M-3 如果星体质量再进一步增 大,则内部电子势必被压缩成 相对论性电子、当达到极相对 Me 论情形,压强与密度的3次方 图4,2 成比例,于是有 ~pR~是R, 即 GM心E~hcKrN~Rnc, R (4.38) 或 GM~NPhc. (4.39) 这表明,如超过临界质量M。时,则质量与半径之间就没有关系 了,即引力大于抵抗压缩的电子气压力,星球就要压垮。所以, 观察到的白矮星质量一定有一临界值,在此临界质量以下的星 体,其深层内部是极相对论电子,表面或外层电子是非相对论电 子,以此来与引力抗衡。 估计白矮星的临界质量是不困难的.熟知原子核是由中子、 质子组成的,每个核子较电子重2000倍,故恒星质量均可认为是 核质量组成的.对于氢,每一个电子就有一质子,对于氨或者更 重的核则每个电子大约相应有两个核子,故 GM:~( M。) mp·t hC, (4.40) 其中p代表质子的质量.而 32

核子数 t。= 电子数 对于氢,。=1,对于氮等,n,=2. 所以临界质量 M.成()(207)月× x(1.0r~1.7Mo. (4.41) 虽然这样估很粗糙,但它却能判断出白矮星是由哪种核物 质组成的.详细计算表明,如果是由氢构成白矮星,则M。~5.6 M⊙,由氦构成,M.一1.4Mo.根据天文观察,所有的白矮星的 质量都不超过1,4M⊙·它表明白矮星是热核燃料氢烧尽后,转化 为氦的星体.如质量超过1.4M。,星体将进一步受到压缩,原子 核内的核子也被挤压出米,电子碰撞质子构成了中子.所以,当 M。~2M。就形成了中子星.如果质量超过2.2M。,星体将继续 受到引力的压缩,尽管有核子间的斥力,也无济于事.因为斥力 越大,能量将越大,这种能量本身又是引力源,会进一步导致星 体塌缩.所以,这使人们相信黑词是存在的. 以上是仅考虑电子气的因紫,至于其他因素均可被忽略,这 是由数量级估计做出的结论. 这些因素有: (i)温度效应大约为102一103电子伏, (i)核子动能大约为电子动能的10-3, (ii)势能的涨落约为10°电子伏, 而白矮星内的简并电子的动能为10电子伏.故相比之下, 其他因素是完全可以忽略的. 例2普通导体中,电子的热力学函数、 在普通导体中,原子菲列是紧凑的.电子的动能约为数个电 子伏,其大小为10厘米 33

假设地球表面温皮为300K,热能就相当于0电子代.它比电 子的动能小得多,故可认为导体中的电子是非常简并的。在普通 固体中势能与动能相近。在非导体中的电子就不能任意地运动. 在导体中,在布里渊区运动的电子可认为是自由的.在这里不去 详细研究导体的具体性质,我们只是对电子构成的费米子系统进 行统计 每个粒子的吉布斯热力势分=“≈e:(电子伏量级),而 室温T一品电子伏显然, e芹e《1可以认为是军. (4.42) 由前面证明的,=。十,其中x三7,知 T=0, 故每一模式的平均电子数呈一阶跃函数: j1当e<4时, n,={0当e>4时. (4.43) T=0 在低温时,。的微商是和δ函 数差不多的,如图4.3所示, T40 a&=d(e-). (4.44) dne D d.e 当计算T年0K时的热力学函数时, 一4 应该考虑kT的影响,不过eT实 花太小,可以略去 图4.3 当e=0时,n,=1, 34