
考虑到三维方向V=L3→∞时 (2.51) 再对螺旋度求利 (2.52) 由(2.35)式可求出能t E=一 a ∂8 InQ=shwe-ai k之1e8m. (2.53) 当V-∞,将(2.53)式写成积分: E- 2V ho 8 (2.54) 先对立体角积分,得北4x囚子,再利用变数变换最后得到 E站(日) 其中x=Bna. π2kT4V 15c3h3, (2.55) (2.55)式表明黑体的能量与B“成反比.但从实验上我们知道黑体 的能量与纯对温度T成正比,这就证明了T就是绝对温度 例2导证普朗克公式. 配分函数中每一项都是相应态的相对几率.由黑体辐射的配 分函数知 Q=I(1+eo+e8*0+…). (2.56) K. 如果在光子的分布{nk,1}中,只考虑某一特定模式K,2的光 子,而不管其他光子的模式时,那么就有以下的相对几率: K,1模式的光子数nK,4三 2 3 对应的行对几率为: e-日春· e-26片u g-58若■ 15

因此,我们可以从配分函数中,瑕出任一模式光子的信息,假 如,我们要问某种模式K,入的光子的平均数耳元k.A,立即可以写出 1:eB0+2ez9t0+3e-方0十… 元k,A=i+e0十e90+e9B和+ -a a(Bho)Inl+e+ a (Bno)In[1-es"] (2.58) 这就是著名的普朗克公式 例3系统能量的涨落. 设任-一系统有能量交换,温度虽固定,但能量E并不固定. 根据标准的统计涨落公式有 (AE)=∑P(E-E)'=〈E〉-〈E, (2.59) 其中 E=∑PEi=〈E). 而 2器-公Eg5-E (2.60) 从(2.60)式可知1Q对B的一次微商就是负的能量平均值.更巧 妙的是对B的二次微商就是能量张落的平方, 器-空所。+日器2治Ee西, =∑PE号-〈E) =(△E). (2.61) 再由(2.60)和(2.61)式可得 4-8器-r(器)=7C (2.62) 16

故能量的相为对涨落为 授-√-o(N (2.63) 由于C,和E都与N成正比,因此只要N足够大能量的相对涨落就 趋于零,所谓N足够大,使得热交换项比起本身可忽略即可,不 一定要求W一定非常大的数甘.因此,这一结论,对任何系统都 是适用的. 小结:到这里,我们得到一个相当广泛的结论:对任何一力 学系统,只要知道这个系统的哈密顿量,并且该系统是与热库有 热交换的,对系统也不做过苛的要求,即不一定包括有102”量级 的粒子,唯一的要求是热交换能量比其木身的能量小得多.那么 就可按以下程序计算一·切热力学函数 (a)先写出系统的哈密顿量H. H (b)计算算符eT的迹,即求出配分函数 E Q=3e T」 =tracee kT (c)山F=一TinQ计算出系统的亥姆霍兹自由能.再对 F进行各种变量的微商,即可得出一切的热力学函数, 在这里对哈密顿量H的要求并无限制,它可能是很复杂的, 但唯一要求就是热交换项可被忽略,以上的办法才是正确的.正 明这个结论用到的唯一假设就是(1.4)式, 在证明过程中,关键是引入了“正则系综”的概念,它被想 像成由M个系统组成的.这是做统计问题所必须的,但并不是一 个假设.这样计算几率P,只有当M(系统数)→∞才是正确的 用这种广泛处理问题的方法,可定出由热力学无祛确定的绝对零 度时的嫡值 应该看到,在这里我们是不论系统的复杂程度一并加以解决 的.如果肖先对系统中的粒子进行讨论,并用自由粒子来展开, 17

那会无法摆脱自由粒予的框框,将会反笼无穷的.所以广泛的处 理方法并不是复张的,反而是简单的. 另外一种方法,是从经典统计方学出发.丁经典统计力学 是复杂的,它的变数连续性带来麻烦.从量子统计开始就简单、 明确.因量子统计状态是分立的、可数的.在经典统计中碰到的 是连续的变量:,dx,…,由一组)“义坐标变换成另一组广义坐标 时,雅可俾行列式引:不一定等丁1.体积是与所用的坐标有关的, 相空间又是对何丛标言?因此引用相空间的定义也是有困摊 的,所以经典统计本身就有名混之处 自然界的某木原理是简单的,应州却很“泛、知朵我们找到 的基本假设是简单的,而应用广泛,那无凝是重要的.现在我们 君到做为理论物理的分皮之一,统计力学确实具有这种特色 S3 巨正则系综 巨正如则系综是推广了的正则系综, 气 它是月来研究不但交换能童,而且交换 粒子的系统.知水与空气之间交换水分 子,在这里水分子数是不固定的.吉布 斯为了研究这类交换粒子的过程,把热 力学公式推}为: 图3.1 dE=-pdy+Tds+udN.(3.1) 其中N是粒子数,“是每个粒子的吉布斯热力势,或称这种 粒子的化学势, G (3.2) 在这里我们引用了热力学公式(3,1)并不表明统计力学依赖 于热力学.对统计力学,本身完全可以自成体系的,我们引入热 力学公式是说明可以从巨正则系综导出这些热力学公式来, 假设由体积'相等的M个相同的系统组成的系综,每个系统 18
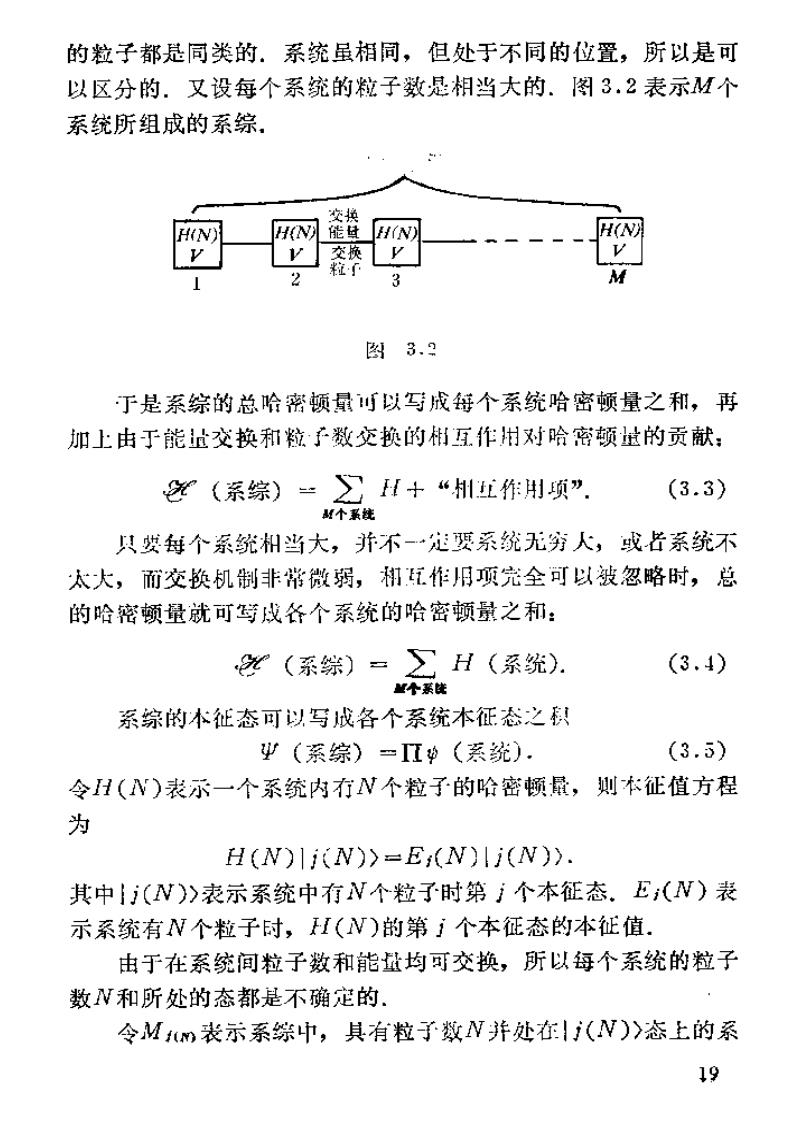
的粒子都是同类的.系统虽相同,但处于不同的位置,所以是可 以区分的.又设每个系统的粒子数是相当大的.图3.2表示M个 系统所组成的系综。 能旦 交换 图3. 丁是系综的总哈密顿量以战每个系统哈密顿量之和,再 加上由于能止交换和粒子数交换的相互作州对哈密顿啦的贡献: (系综)二之H+“州红作用项”. (3.3) M个最统 只要每个系统州当大,并不-…定要系统无穷人,或片系统不 太大,而交换机制非常微弱,初五作旧顶完全可以被忽略时,总 的哈密颜量就可写成各个系统的哈密顿量之和: (系综)=∑H(系统). (3,4) M个系饯 系综的本征态可以写成各个系统本征态之积 Ψ(系综)=几的(系统). (3.5) 令H()表示一个系统内行N个粒子的哈密顿量,知本征值方程 为 H(N)i(N)>=E;(N)i(N)>. 其中{j(N)》表示系统中有V个粒子时第j个本征态.E(N)表 示系统有N个粒子时,I(V)的第j个本征态的本征值! 由于在系统间粒子数和能量均可交换,所以每个系统的粒子 数N和所处的态都是不确定的 令M表示系踪中,具有粒子数N并处在(N)》态王的系 19