
x x'e-2 dx x x2 e dx 0 =48[haeda] =A2 (2.32) 比较(2.29)式和(2.32)式 (M,一M)2=M-M;=MP, 代入涨落公式得 指√寇√ MP; 度子 厂石=0,当M-→oo时. NMPi 这样证明了当H和F固定时,M→∞,几率的最大分布就是 真实的分布 现在再来讨论B常数的物理意义.山公式(2.17)和(2.18) 知,当系统之间有热交换时,只要可以忽略热接触线对哈密顿量 的贡献,都得到同样的表示式(2.17).这表明不同系统之间B是 相同的.在给出的习题中,读者还可证明由许多不同类的互相有 热接触的系统组成的系综,B也是相同的.因此B具有温度的意 义,由于几率是与BE:呈负指数的关系,B越大,几率越小.B 增大倾向于低能态。这表明B确是一个温度的标记,不过它与我 们通常的温度概念相反,即9越大,温度越低 定义{ 10

写成等式则为 1 在此是玻尔兹曼诈数, k=1.38×10-1尔格/开=8.31×10-5电子伏/开. 以后还要论证T正是绝对湛度 由于人们在近代对分子、原子的结构深入的研究,因此多用 电子伏这个能量单位,如在室温下,T兰300水,它相当于能量 T兰40电子伏. 这是个很容易记的数据,它便丁我们随时了解和比较通常温 度下的物理状态,我们应该记牢它. 从(2.18)式所定义的配分函数知,其巾的每一项表示处在状 态j的相对儿率.这是一个非常重要的函数.在统计力学中,买 要我们有了配分函数Q就可导出一切热力学函数. 定义引!入一函数 F=-kTIn. (2.33) 可以证明,函数F狱是亥奶霍兹自由能(热力学). 为证明它是热力学的亥姆霜兹月由能,让:我们首先证明能聚 的平均值为 -r())=∑P,E,=E: (2.34) 证明:由配分厨数Q的定义知 -a的-8∑Ee-2PE=E. (2.35) 但是 B=KT, dB 所以 (2.36) 11

(2.35)乘(2.36)式得 ainQ E ar 将(2.33)式F的定义代入上式得 -()-nQ-E. 得证, 另外,从热力学知亥姆霍兹自由能存在以下关系: dF热=一SdT-pdV. (2.37) 在此F热、S和p分别表示热力学的亥姆霍兹自中能、熵和压强 扩表体积. 由此可得: -Ta(6)w-r[F(-)7器] -户s+TA =F热+TS=E. (2.38) (2.34)式中,微商是在系统的哈密顿量不变下进行的,即在 体积V和粒子数N不变下求出的.故由(2,38)和(2.34)式可得出 (2.39) 当温度T→0时,系统都处在基态.设基态能量为E。,基态 的简并度为⊙。,配分函数头有一项 E Q京0e (2.40) 从(2.33)式F的定义知,当温度T-→0时, F-E。-kTln0o, (2.41) 12

另由热力学知,当温度T→0时有 F热E。-TSo, (2.42) 其中E。是最低能量,S。是绝对零度时的脑.从热力学本身是无 法定山绝对零度时的嫡值的,尽管能脱斯曾规定绝对零度时的嫡 为零.因此,我们只要规定 S。三kln⊙o, (2.43) 连同(2.39)式就可得出这个结论:在任何温度下统计力学的F就 是热力学的亥姆霍兹白由能F然,即 F=F&. (2.4) 从统计力学观点看,只有在基态不简并的情况下,S。是零.如果 基态是简并的,S就不是零。 以下列举儿个简单的应用例子: 例1论证温度T'就是绝对温度. 由丁黑体中的光子间几乎是没有相互作用的,故可认为光于 气是一一种理想气体*,光子只是通过与黑体的器壁碰撞达到平衡. 因此只要让黑体容器足够火就可忽路光子与容器面的作用.这样 的系统确定的温度无疑最为精确。 考虑一边长为L的立方体容器,如图2.2所示,体积为L 其中的光子状态可以用它的动量K和螺旋性几一士1来描写. 让K.表示具有波数矢量为K,螺旋性为1的光子数目, nk.4=0,1,2,…. 因此只要给定一组集{k,a},就确了系统的一个态.系统的 总能量 E-∑ nk.ah, (2.45) {K,} 其中0为角频率 目前光子之间的枳互作用的微小盘,可以用母子电动力学计算出来,但是实 验还测量不出这微小爵,即使用最先进的激光技术也未量出.故我们完会可以忽略掉 光子之间的相五作用,而认为它们是理想的光子气. 13
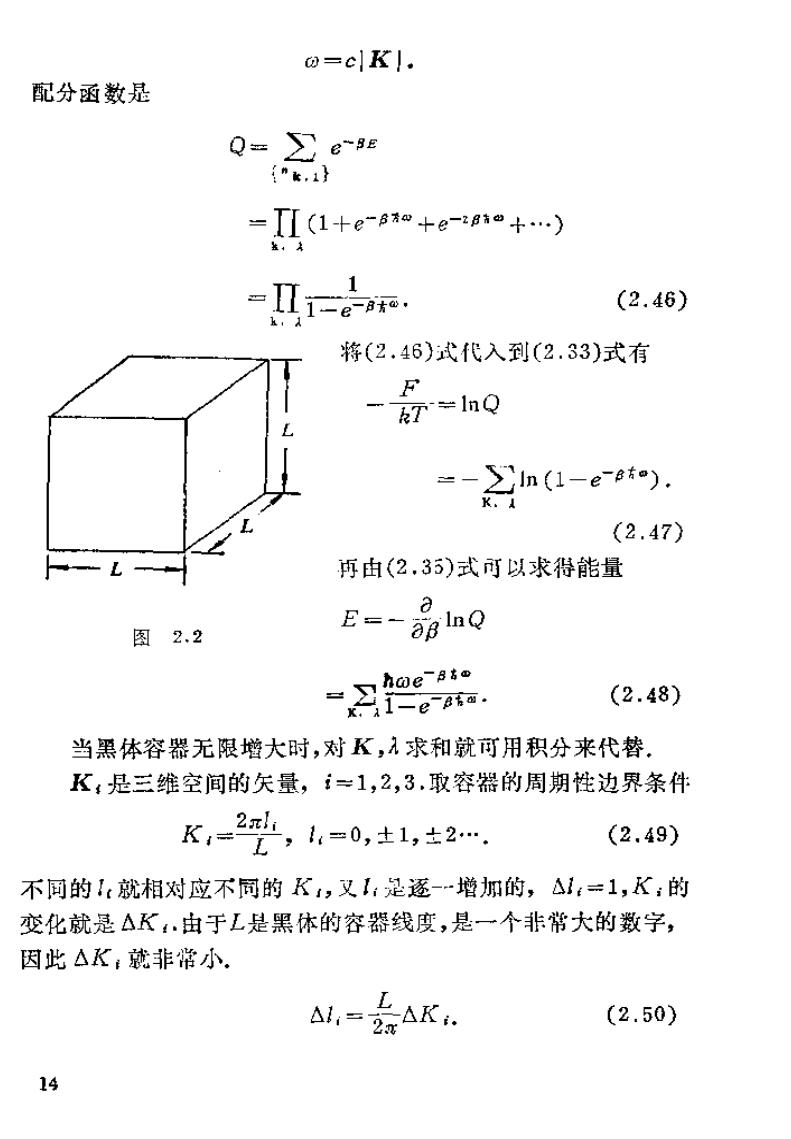
@=c]K. 配分函数是 Q=∑.e8E nk,1} =T[(1-十eB*o+e-28@+…) (2.46) 将(2.46)式代入到(2.33)式有 F T=InQ =2m(1-e). (2.47) 再由(2,35)式可以求得能量 a 图2,2 E=-a弟hQ (2.48) 当黑体容器无限增大时,对K,1求和就可用积分来代替。 K4是三维空间的矢量,i=1,2,3,取容器的周期性边界条件 K-2,=0,±1,2 (2.49) 不同的1:就相对应不同的K1,又【;是逐-一增加的,△1=1,K:的 变化就是△K·由于L是黑体的容器线度,是一个非常大的数字, 因此△K:就非常小. A,=÷AK (2.50) 14