
之和. 正则系综给定后,假设只知道系综总能量为8,但并不]道 某系统处在哪个态,我们要问,某系统处在中;态上的儿率是 多少? 设M裘示在中态上的系统数,E,表示第j个态的能量.显 然,总的系统数 M=2M, (2.5) 系综的总能量 8=M,E,. (2.6) 尽管我们知道了总能耻和总的系统数M,并且给定了一分 布{M},但是各系统的状态仍然没有完全确定.例如,已知有3 个系统在j:态,5个系统在j2态,但是到底哪3个系统在j态,哪 5个系统在2态,还是不确定的.很容易证明,对某一给定分布 {M},系综的态数2为 IM小 (2.7) 证明如下: M个系统所有不同排列的总数是M!,但是在同一状态的系统 之间的交换并不产生新的态,因此,应该把它们除去,于是(2.7) 式得证 现列举一简单的由三个系统构成的小系综为例加以说明,即 M=3. ()如一个系统在j,态,两个系统在j:态,所以系综的态 31 数0-1121 3. (i)如有三个系统在j:态,有0个系统在i:态,所以系综 31_ 的态数2=0131 =1 5

这些简例的果是明显可见的.同理,当M很大时也是正确 的。 由此可知,尽管给定了8,M和分布{M;},系统的状态并不 确定.另一方间,如采仅仅给定了后和M,{M,》分布并不确定, 我们要问,哪种分布《M}的儿率最大?根据(1.4)式的基本假 设,每种分布几率应与所对应的态数2成正比,因为态越多,几 率越大,对分布几率求极大值,就是求2的极大值.利用求微商 的方法并光虑到(2,5)和(2.6)式对M利8给定的约束条件,要引 入两个拉格朗日乘子α和B.所以极值的条件是 a a(∑M)3Me,) aMij Ing-a -=0.(2.8) aMi OM 要淮确计算几落就要要求系综中的系统数很大,但系统本 身不一定很大,任何统计分析问题必须要重复非常多次同样的过 程才能得到较正确的几率.以掷骰子为例,掷骰子的次数越多, 几率就越接近某-一固定数,这见做-·切统计问题的方法,它并不 是一个假设.当M趋向无穷大时,相应地,各M;也趋向无穷大 对于M》1,可以用斯特灵公式(Stirling formula)来近似地代替 阶乘: M1-(0'2a1++a88M+… (2.9) 这一公式收敛得很快,郑使M不很大也是一个很好的近似公式」 读者可以自行证明这一公式.利用斯特灵公式得到 lnQ=MnM-M-∑M,lnM;+∑M. (2.10) 在对?求偏微商时,有两种不同的方法.一种方法是视I 为固定.另一种方法是视M为M:的函数,因此也要对M求偏微 商.不过,所得的结架是一致的,只是α的值相差一个常数.为 简便计,我们采用M面定的方法,得出 6

OIn OM; =一lnM, (2.11) aM 2Mi =1, (2.12) 88=E: a (2.13) 将以上(2.11)、(2.12)和(2.13)式代入(2.8)式得 --In M;-a-BE=0, (2.14) 即 In Mj=-a-BEi, (2.15) 所以 Mj=e-a-BEi. (2.16) (2.16)式表示在正则系综中,在系统数M给定和总能量8周 定的条件下,系统处在第j态上的儿率最大的分布.式中出现了 两个常数a和B,以后对B的物理意义还要讨论, 定义P,表示最大几率分布时,系统处在第j态的几率: e-BE Pi=M (2,17) 2 e-BEj 定义 配分函数Q=∑eE1. (2.18) 它表示各个状态的相对儿率之和.在(2.17)式,配分函数是 作为归一化因子出现的 在求P时就消去了α因子,B因子可以出系统的平均能量 E=哥 (2.19) 来确定, E=古Be. (2.20) 这个等式给出一重要结果:在正则系综中,给定至,而M趋向无 7

限大时,P;和B与M无关. 下面再来证明,在给定系统的和E,当M趋向无穷大时, 以上的几率最大分布就是真实的分布,换言之,涨落趋向于袋 证明如下: 试考虑一函数 f=f(M)=ln2-a∑M-B∑ME1,(2.21) 手达到极值的条件为 af OM; =0. (2.22) 达到极值时,M,=MP;三亚;,P;与M无关. 而 a'f 8'InQ 1 aMaM “i,<0. (2.23)》 由于f的第二项和第三项均为M;的一次式,故对M:二阶以上的 微商均为零。只剩下第一项取不为零的负值.这表明极值是稳定 的. f对M;每求一次微商,其分母就增加一个M:因子.由于 →c∞,M→c∞,所以高次微商很快地趋向零. 用泰勒级数把f(M)在及附近展开: )-)+子 af (M;-)+ +2号影M,-r+ (2.24) =-f(及)-22MP(M1-,)× x{1+o(x)以 (2.25) 8
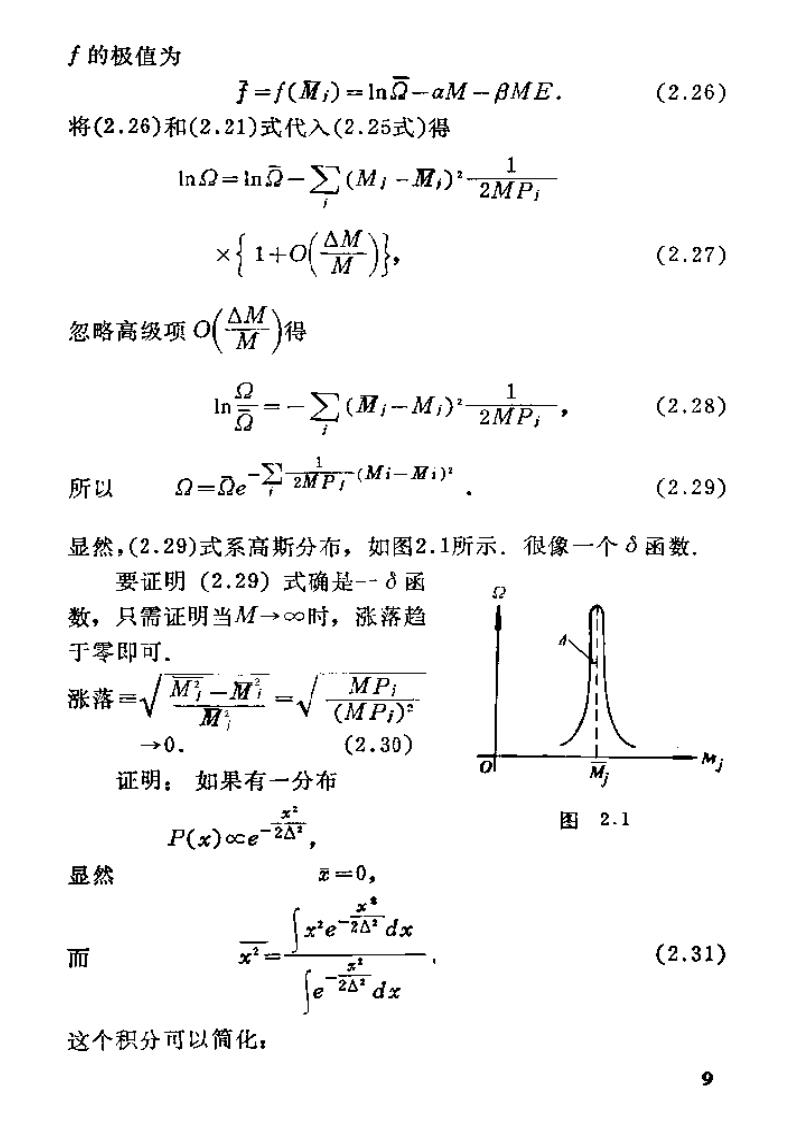
手的极值为 子=f()=ln-aM-BME. (2.26) 将(2.26)和(2.21)式代入(2.25式)得 ln2=n2-∑(M1-,)22MP, ×{1+o(以, (2.27) 忽略高级项0(器)舟 ∑(及1-M)22MP,, (2,28) 所以 Q=DeP (Mi-i) (2.29) 显然,(2.29)式系高斯分布,如图2.1所示.很像一个8函数. 要证明(2.29)式确是--6函 2 数,只需证明当M→∞时,涨落趋 于零即可. 涨落三√ 福--√ MPi (MP)? →0. (2.30) 0 M 证明:如果有一分布 M P(x)ce-2」 图2.1 显然 2=0, xt x'e 26dx 而 x- (2.31) e 2A dx 这个积分可以筒化: 9