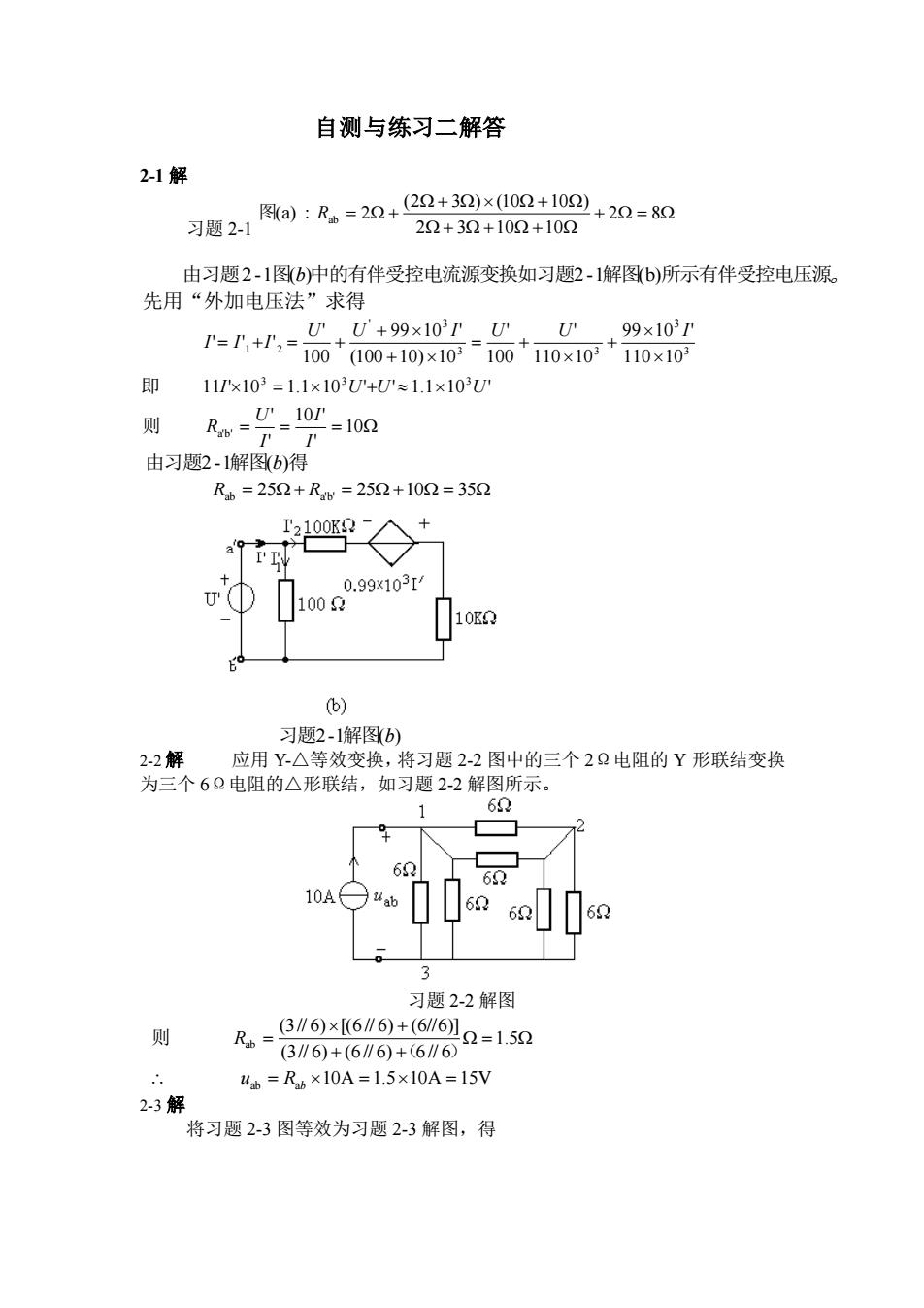
自测与练习二解答2-1解图(a) : Rs =22+(22+30)x(102+100)2+22=82习题2-120+30+100+100由习题2-1图(b)中的有伴受控电流源变换如习题2-1解图(b)所示有伴受控电压源。先用“外加电压法”求得U"UU+99×10"99×1031I=I+I2=(100+10)×103100110×103110×103100即11/x103=1.1x103U'+U'~1.1x103UU10则=102Rab =T-1由习题2-1解图(b)得Rab=252+Rab=252+102=35212100KS2I'IJ0.99x1031100Q10KQ(b)习题2-1解图(b)2-2解应用Y-A等效变换,将习题2-2图中的三个2Q电阻的Y形联结变换为三个6Q电阻的△形联结,如习题2-2解图所示。6021626010A593习题2-2解图(3 // 6)×[(6 // 6) +(6//6)]则Rab :2=1.5(3 // 6)+(6 // 6) +(6 // 6)..u=Rb×10A=1.5×10A=15V2-3解将习题2-3图等效为习题2-3解图,得
自测与练习二解答 2-1 解 习题 2-1 + = + + + + + = + 2 8 2 3 10 10 (2 3 ) (10 10 ) 图(a) : Rab 2 由习题2 -1图(b)中的有伴受控电流源变换如习题2-1解图(b)所示有伴受控电压源。 先用“外加电压法”求得 10 ' 10 ' ' ' 即 11 ' 10 1.1 10 ' ' 1.1 10 ' 110 10 99 10 ' 110 10 ' 100 ' (100 10) 10 99 10 ' 100 ' ' ' ' a'b' 3 3 3 3 3 3 3 ' 3 1 2 = = = = + + = + + + = + = + I I I U R I U U U U U I U U I I I I 则 由习题2 -1解图(b)得 Rab = 25 + Ra'b' = 25 +10 = 35 习题2-1解图(b) 2-2 解 应用 Y-△等效变换,将习题 2-2 图中的三个 2Ω电阻的 Y 形联结变换 为三个 6Ω电阻的△形联结,如习题 2-2 解图所示。 习题 2-2 解图 = + + + = 1.5 (3// 6) (6 // 6) 6 // 6 (3// 6) [(6 // 6) (6//6)] ab ( ) 则 R uab = Rab 10A =1.510A =15V 2-3 解 将习题 2-3 图等效为习题 2-3 解图,得
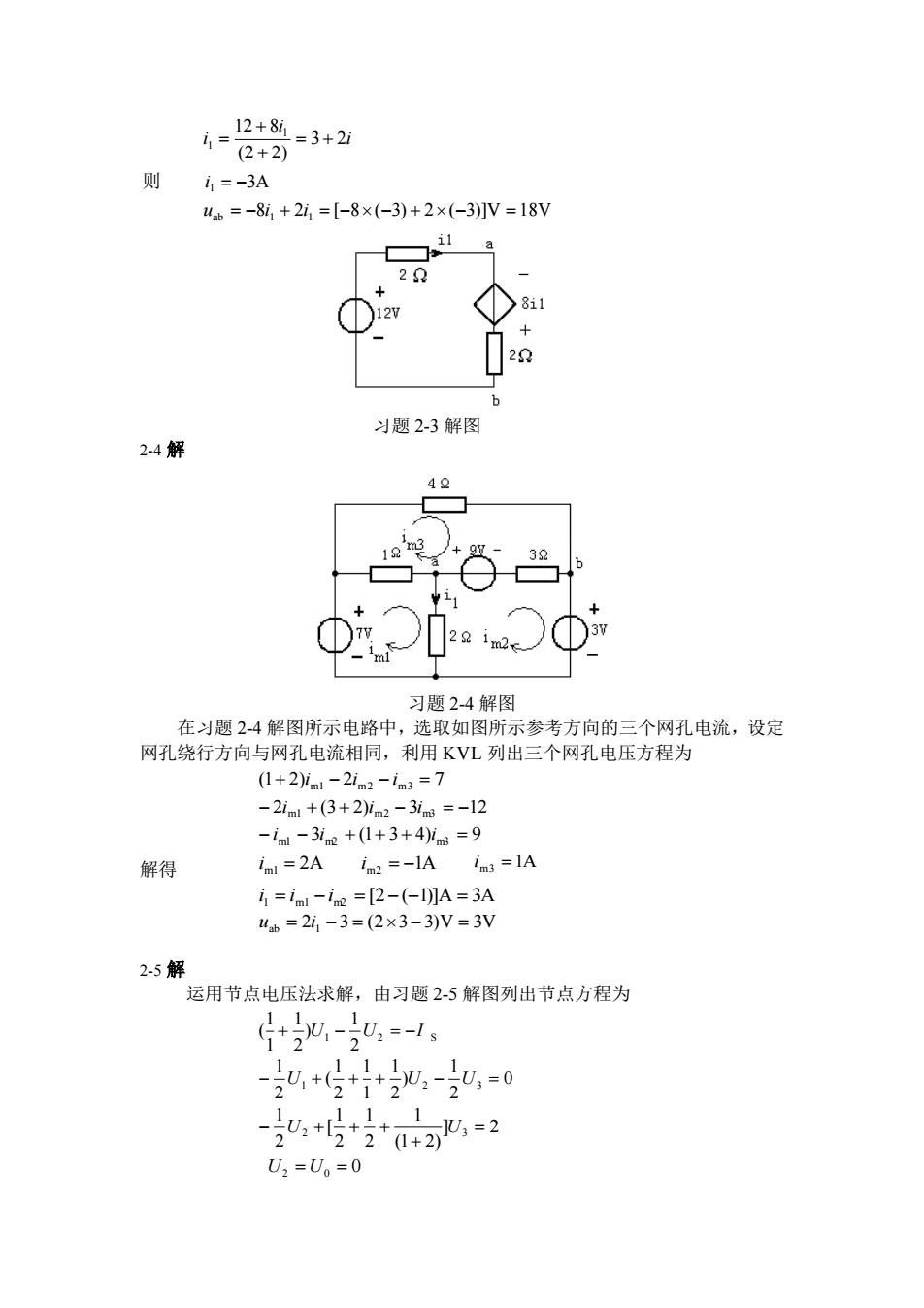
12 + 8i,1=3+2ii=(2 + 2)则i = -3Auab = -8i, + 2i, =[-8 ×(-3) + 2 ×(-3)]V = 18Vi12.0X12V252b习题2-3解图2-4解42m31239习题2-4解图在习题2-4解图所示电路中,选取如图所示参考方向的三个网孔电流,设定网孔绕行方向与网孔电流相同,利用KVL列出三个网孔电压方程为(1+2)iml-2im2 -im3 =7-2iml +(3+2)im2 -3im =-12-iml-3im+(1+3+4)im=9im3 =1Aim=2Aim2=-1A解得i =iml-ime =[2-(-1)]A=3Auab=2i,-3=(2×3-3)V=3V2-5解运用节点电压法求解,由习题2-5解图列出节点方程为11-(+-)U,--u, =-I s12211111U,+(++=)U-U, =022212211U, +[JU, = 2-222(1 + 2)U, =U.=0
8 2 [ 8 ( 3) 2 ( 3)]V 18V 3A 3 2 (2 2) 12 8 ab 1 1 1 1 1 = − + = − − + − = = − = + + + = u i i i i i i 则 习题 2-3 解图 2-4 解 习题 2-4 解图 在习题 2-4 解图所示电路中,选取如图所示参考方向的三个网孔电流,设定 网孔绕行方向与网孔电流相同,利用 KVL 列出三个网孔电压方程为 (1 2) 2 7 + im1 − im2 − im3 = 2 (3 2) 3 12 − im1 + + im2 − im3 = − 3 (1 3 4) 9 − im1 − im2 + + + im3 = 解得 2A im1 = 1A im2 = − 1A im3 = [2 ( 1)]A 3A i 1 = im1 −im2 = − − = 2 3 (2 3 3)V 3V uab = i 1 − = − = 2-5 解 运用节点电压法求解,由习题 2-5 解图列出节点方程为 2 1 ) 2 1 1 1 ( 1 2 S + U − U = −I 0 2 1 ) 2 1 1 1 2 1 ( 2 1 − U1 + + + U2 − U3 = ] 2 (1 2) 1 2 1 2 1 [ 2 1 2 3 = + − U + + + U 0 U2 = U0 =
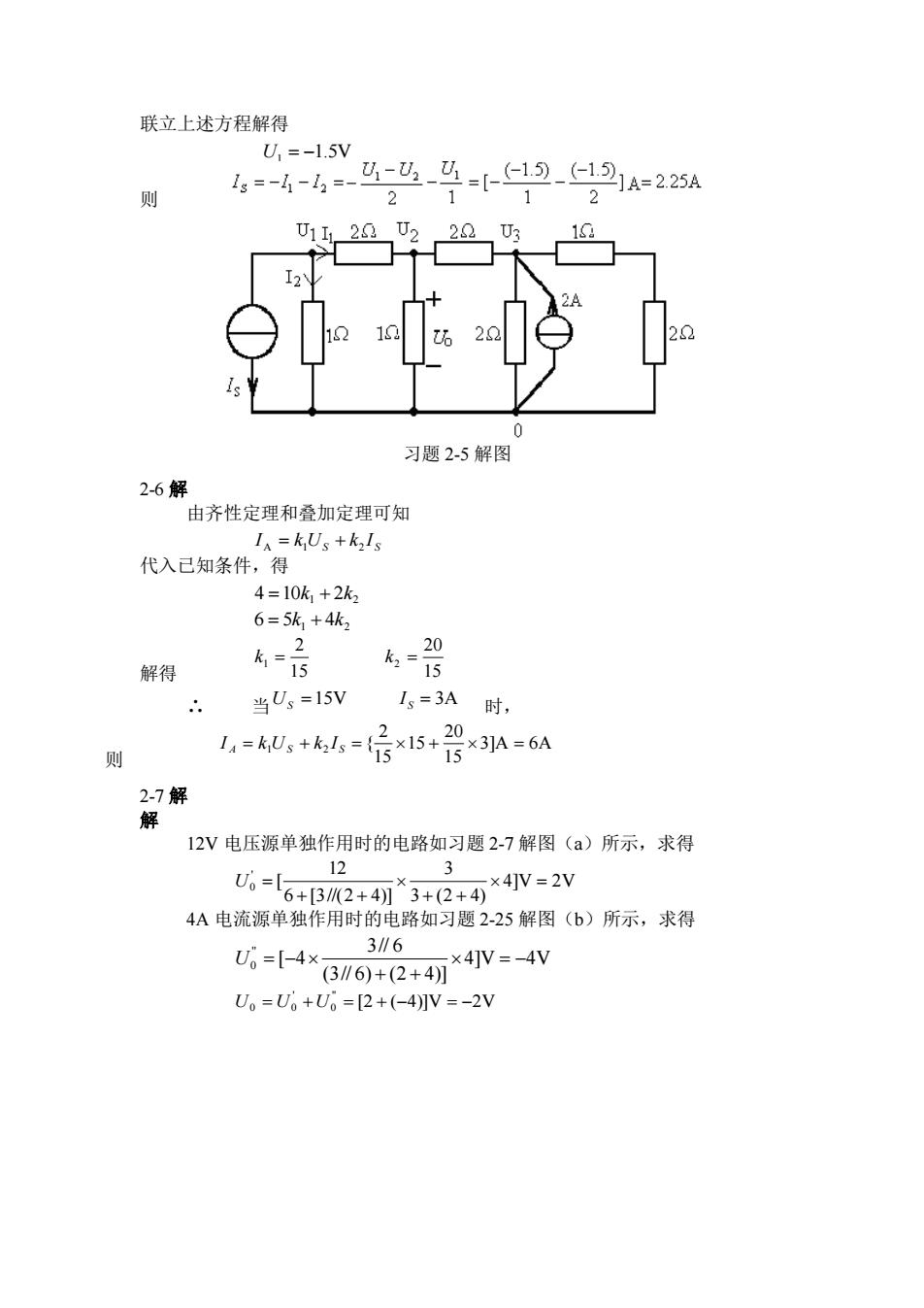
联立上述方程解得U, = -1.5VU,U,-U,(-1.5)(-1.5)=2.25AIg =-1 -12 =-2112则U215U1I,2922U3I21+2A192222102UoIs0习题2-5解图2-6解由齐性定理和叠加定理可知I =k,U、+k,I代入已知条件,得4= 10k, +2kz6=5k, +4kz=220k, =1515解得当U,=15VI,=3A时,.:×15+20.2I,=kUs+k,Is=(×31A=6A15则152-7 解解12V电压源单独作用时的电路如习题2-7解图(a)所示,求得123U。=[X4/V=2V6 +[3 //(2 + 4)]*3 +(2 + 4)4A电流源单独作用时的电路如习题2-25解图(b)所示,求得3// 6U, =[-4x×4IV=-4V(3 // 6)+(2 +4))U。=U。 +U。=[2 +(-4)]V = -2V
联立上述方程解得 1.5V U1 = − 则 习题 2-5 解图 2-6 解 由齐性定理和叠加定理可知 A 1 S 2 S I = k U + k I 代入已知条件,得 4 10 2 1 2 = k + k 6 5 4 1 2 = k + k 解得 15 2 k1 = 15 20 k2 = ∴ 当 =15V US = 3A S I 时, 则 3]A 6A 15 20 15 15 2 { I A = k1US + k2 I S = + = 2-7 解 解 12V 电压源单独作用时的电路如习题 2-7 解图(a)所示,求得 4]V 2V 3 (2 4) 3 6 [3//(2 4)] 12 [ ' 0 = + + + + U = 4A 电流源单独作用时的电路如习题 2-25 解图(b)所示,求得 4]V 4V (3// 6) (2 4)] 3// 6 [ 4 '' 0 = − + + U = − [2 ( 4)]V 2V '' 0 ' U0 = U0 +U = + − = −
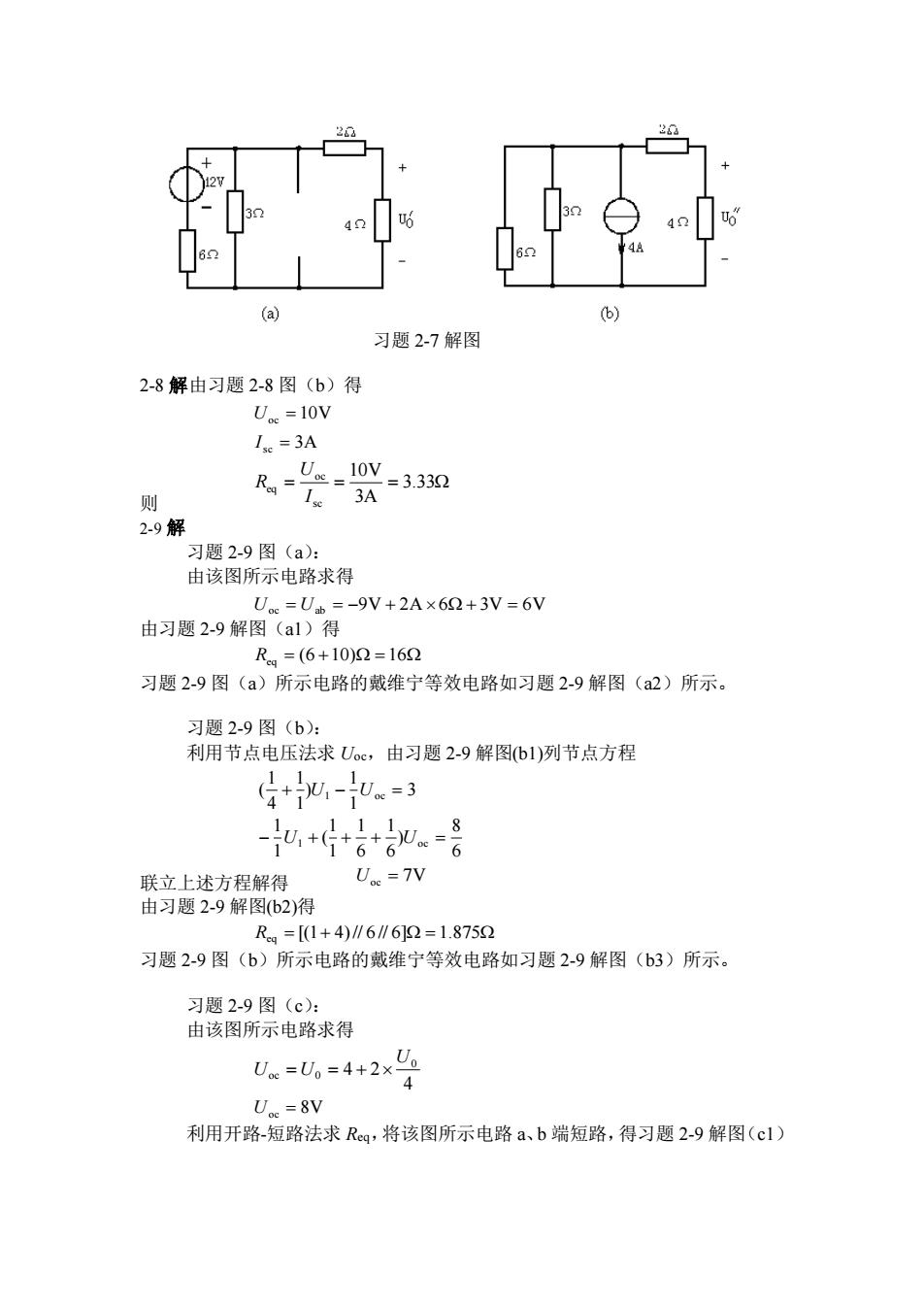
20UO404.8(a)(b)习题2-7解图2-8解由习题2-8图(b)得U.c=10VIs.=3AUo._10VR.=3.33Q-3AIs则2-9解习题2-9图(a:由该图所示电路求得U.=Ub=-9V+2A×62+3V=6V由习题2-9解图(al)得R..= (6+10)Q=162习题2-9图(a)所示电路的戴维宁等效电路如习题2-9解图(a2)所示。习题2-9图(b):利用节点电压法求Uoc,由习题2-9解图(b1)列节点方程G+u.-jus =3.811+U-U, +(G6166U.. =7V联立上述方程解得由习题2-9解图(b2)得Reg =[(1+4)// 6 // 6]Q=1.8752习题2-9图(b)所示电路的戴维宁等效电路如习题2-9解图(b3)所示。习题2-9图(c):由该图所示电路求得Uo =U。=4+2×g4U..=8V利用开路-短路法求Reg,将该图所示电路a、b端短路,得习题2-9解图(c1))
习题 2-7 解图 2-8 解由习题 2-8 图(b)得 Uoc = 10V I sc = 3A 则 3.33 3A 10V sc oc eq = = = I U R 2-9 解 习题 2-9 图(a): 由该图所示电路求得 Uoc = Uab = −9V + 2A 6 + 3V = 6V 由习题 2-9 解图(a1)得 (6 10) 16 Req = + = 习题 2-9 图(a)所示电路的戴维宁等效电路如习题 2-9 解图(a2)所示。 习题 2-9 图(b): 利用节点电压法求 Uoc,由习题 2-9 解图(b1)列节点方程 3 1 1 ) 1 1 4 1 ( + U1 − Uoc = 6 8 ) 6 1 6 1 1 1 ( 1 1 − U1 + + + Uoc = 联立上述方程解得 Uoc = 7V 由习题 2-9 解图(b2)得 [(1 4)// 6 // 6] 1.875 Req = + = 习题 2-9 图(b)所示电路的戴维宁等效电路如习题 2-9 解图(b3)所示。 习题 2-9 图(c): 由该图所示电路求得 4 4 2 0 oc 0 U U = U = + Uoc = 8V 利用开路-短路法求 Req,将该图所示电路 a、b 端短路,得习题 2-9 解图(c1)
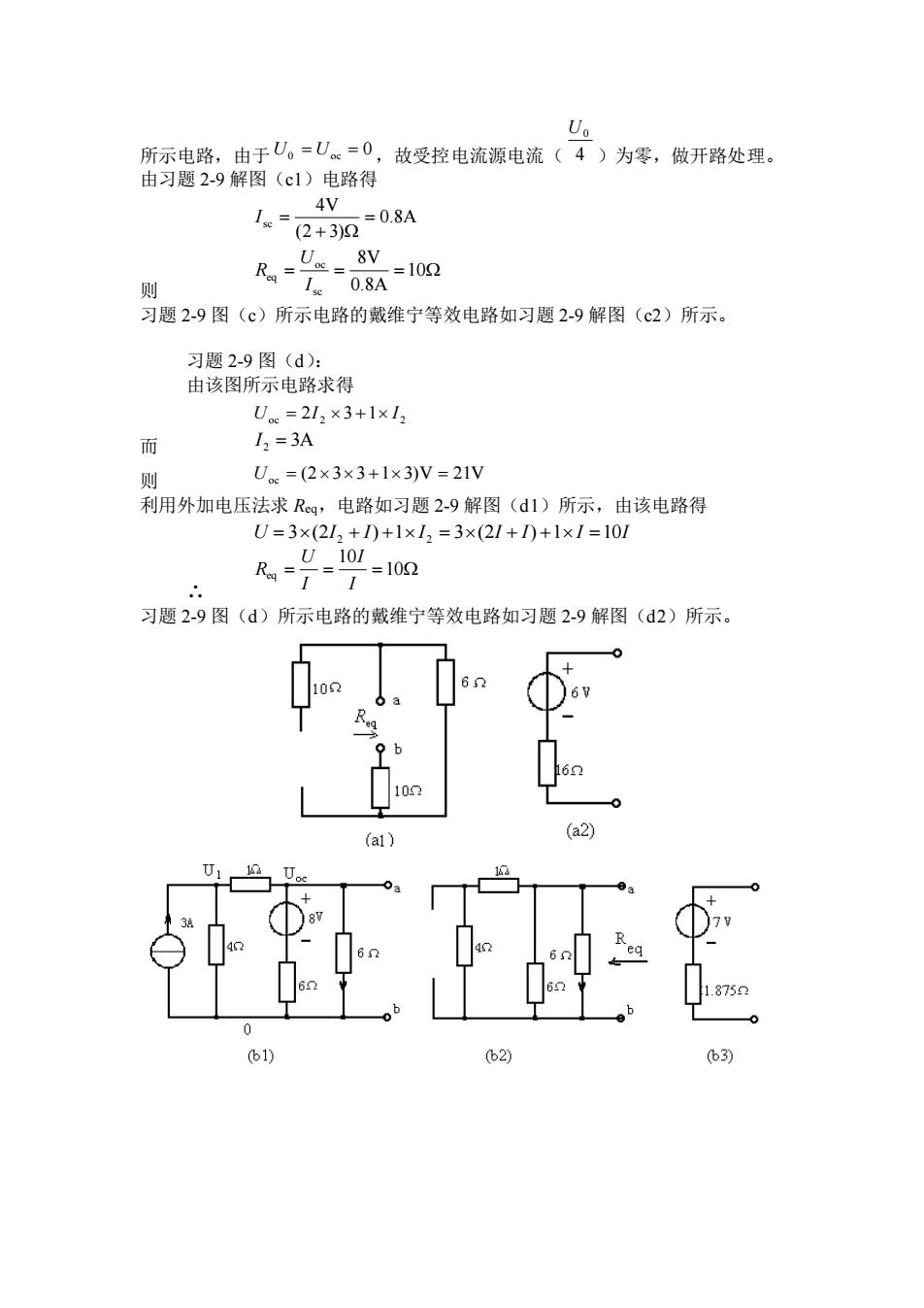
U。所示电路,由于U。=U=0,故受控电流源电流(4)为零,做开路处理。由习题2-9解图(c1)电路得4V=0.8AIse =(2 + 3)2Uo=8VRe==102Is0.8A则习题2-9图(c)所示电路的戴维宁等效电路如习题2-9解图(c2)所示。习题2-9图(d):由该图所示电路求得U.=2l,×3+1x1,I, =3A而U.。=(2×3×3+1×3)V=21V则利用外加电压法求Reg,电路如习题2-9解图(d1)所示,由该电路得U=3×(21, +I)+1×1, =3×(21+D)+1×I=101U101Req==102II.:.习题2-9图(d)所示电路的戴维宁等效电路如习题2-9解图(d2)所示。6.26VRob162102(a2)(al)U16eg6.521.8750(b1)(b2)(b3)
所示电路,由于 U0 = Uoc = 0 ,故受控电流源电流( 4 U0 )为零,做开路处理。 由习题 2-9 解图(c1)电路得 0.8A (2 3) 4V sc = + I = 则 10 0.8A 8V sc oc eq = = = I U R 习题 2-9 图(c)所示电路的戴维宁等效电路如习题 2-9 解图(c2)所示。 习题 2-9 图(d): 由该图所示电路求得 oc 2 2 3 1 2 U = I + I 而 I 2 = 3A 则 Uoc = (233 +13)V = 21V 利用外加电压法求 Req,电路如习题 2-9 解图(d1)所示,由该电路得 U 3 (2I I) 1 I 3 (2I I) 1 I 10I = 2 + + 2 = + + = ∴ 10 10 eq = = = I I I U R 习题 2-9 图(d)所示电路的戴维宁等效电路如习题 2-9 解图(d2)所示