
或者从直角坐标系中的柯西-黎曼方程(1.3.3)出发,按照变换公 式(1.1.2)变换到极坐标系,也可得到极坐标系中的柯西-黎曼方 程(1.3.4). 习 题 试推导极坐标系中的柯西-黎曼方程(1.3.4). S1.4解析函数 若函数f()在点z。及其邻域上处处可导,则称f(x)在。点 解析.又若f(z)在区域B上每一点都解析,则称f(x)是区域B上 的解析函数.可见,函数若在某一点解析,则必在该点可导.反之却 不一定成立.例如,函数f(x)=|之2仅在x=0点可导,而在其它 点均不可导,由解析性的定义可知,它在x=0点并且在整个复平 面上处处不解析.这表明函数在一点可导与解析是不等价的.但 是,函数若在某区域B上解析,意味着函数在区域B上处处可 导.因此,函数在某区域上可是与解析是等价的 解析函数是一类具有特殊性质的复变函数,在物理学中有着 重要的用途.下面介绍解析函数的几条主要的性质, l.若函数f(x)=u十iw在区域B上解析,则 u(x,y)=C1,v(z,y)=Ca (C,C2为常数)是B上的两组正交曲线族 事实上,将柯西-黎曼条件(1.3.3)两边分别相乘,得 au av 9x9x ey ay 即 ou aveu av axax ayay 二0. (1.4.1) 这是说,梯度7其直角坐标分量为和影 跟梯度v其直角 坐标分量为和)正交.我们知道,7u和口分别是曲线u= ·13

常数”和“v=常数炒的法向矢量,因而(1.4.1)表明“u=常数”和“v 一常数”是互相正交的两曲线族 2.若函数f(z)一u十iw在区域B上解析,则4v均为B上的 调和函数.[“调和函数”一词说的是,如果某函数H(x,y)在区域 B上有二阶连续偏导数,且满足拉普拉斯方程口H=0,则称 H(x,y)为区域B上的调和函数.门 §2.3将证明,某个区域上的解析函数在该区域上必有任意 阶的导数这样,二阶偏导数整股·和导 当然 都存在且连续、现在拿柯西黎曼方程 =, ax ay ay ax 的前一式对x求导,后一式对y求导,然后相加,这就消去了v而 得到 + ay20. (1.4.2) 同理消去“可得 20. (1.4.3) 这是说,u(x,y)和v(x,y)都满足二维的拉普拉斯方程,换句话说, 它们都是调和函数.由于它们是同一个复变函数的实部和虚部,所 以又特别叫作共轭调和函数. 这样,若给定一个二元的调和函数,我们可以把它看作某个解 析函数的实部(或虚部),利用柯西-黎曼条件求出相应的虚部(或 实部),这也就确定了这个解析函数. 为确定起见,设给定的二元调和函数u(x,y)是解析函数的实 部,试求相应的虚部(x,y).首先,二元函数(x,y)的徽分式是 dud+dy. 根据柯西-黎曼条件,上式可以改写为 ·140

(1.4.4) ey 易于验证上式是全微分.事实上, 32u au日 ay 0y2 ax2 于是,可用下列方法计算出v(x,y)=du. (1)曲线积分法全微分的积分与路径无关,故可选取特殊积 分路径,使积分容易算出. (2)凑全微分显式法把微分式(1.4.4)的右端凑成全微分显 式,v(x,y)自然就求出了. (3)不定积分法 这些方法同样适用于从虚部v求实部“的情况.具体运作请 见下面的例题. 例1已知解析函数f(z)的实部u(x,y)=x2一y2,求虚部和 这个解析函数 解首先验证“是调和函数,我们有 因此,“确是某个解析函数的实部. (1)曲线积分法 先计算u的偏导数 =2x, ar 3u=-2y. o 根据柯西-黎曼条件,我们有 av ax -2y, 30二2x. ey 于是 dv=2ydx+2xdy. 右端应是全微分,积分值 (z.y) v= 2ydx+2xdy+C· ·15-
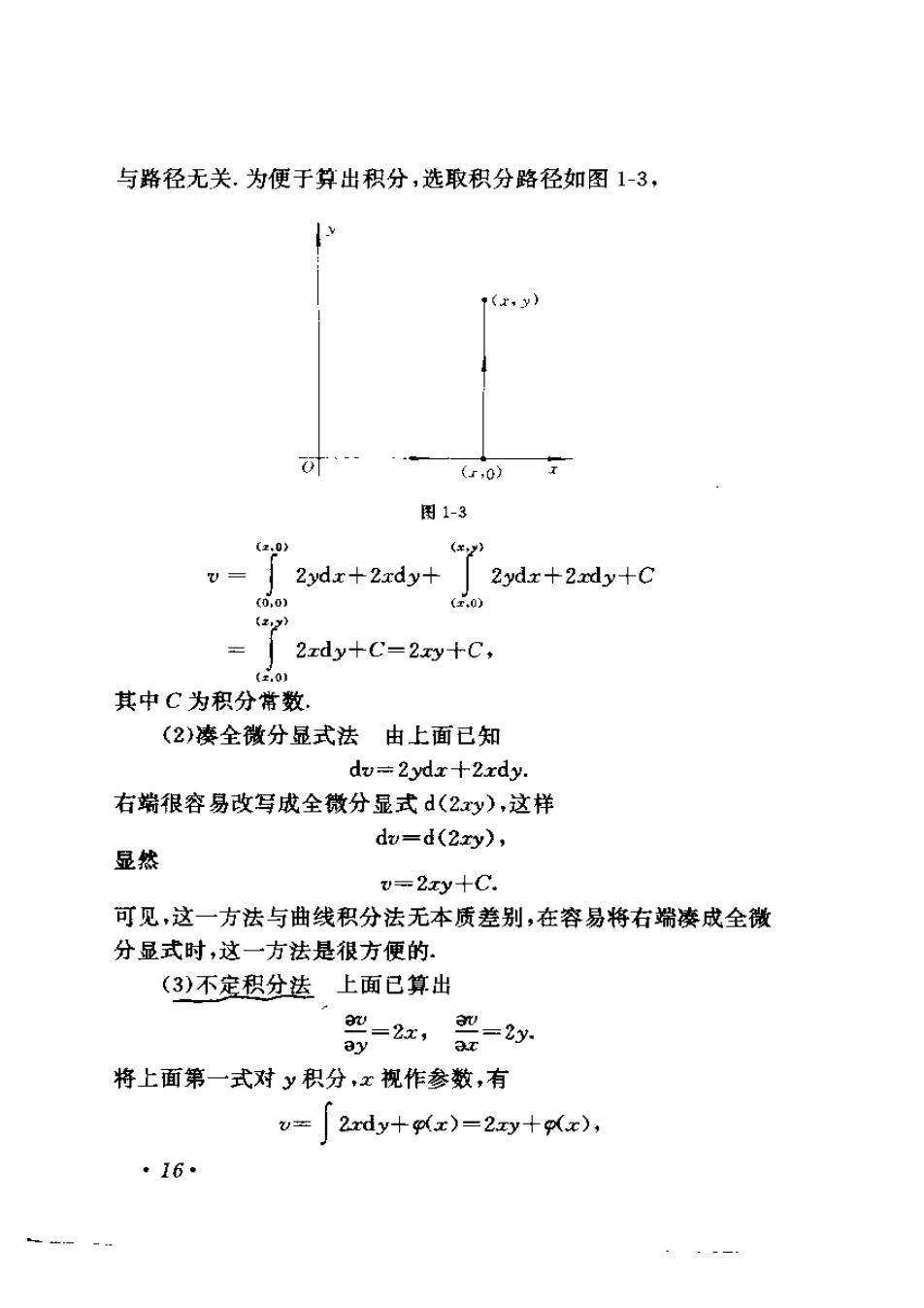
与路径无关.为便于算出积分,选取积分路径如图1-3, (x.y) (,0)x 图1-3 (z,0 (¥y》 v=2ydx+2xdy+2ydx+2xdy+C (0,0) (r,0) 〔2,y3 =2xdy+C=2xy+C, {z,01 其中C为积分常数. (2)凑全微分显式法 由上面已知 dv=2ydx12xdy. 右端很容易改写成全微分显式d(2y),这样 dv=d(2zy), 显然 v=2xy十C. 可见,这一方法与曲线积分法无本质差别,在容易将右端凑成全微 分显式时,这一方法是很方便的. (3)不定积分法上面已算出 0=2x, ay 器=2 将上面第一式对y积分,x视作参数,有 v= 2xdy+px)=2xy十g(x), ·16

其中(x)为x的任意函数,将上式两边再对x求导, =2y十9. 由柯西-黎曼条件知,(x)=0,从而p(x)=C(常数),因此 v=2xy+C. 最后,我们得到所求的解析函数为 f(x)=x2-y2+i(2xy+C)=之2+C. 例2已知解析函数∫(:)的虚部v(x,y)=W一x十√x2+y2, 求实部u(x,y)和这个解析函数f(之. 解 偏导数二和的计算比较费事,试改用极坐标系, =√/-osp叶e=Vp1-c0s9=√2psin罗. 下面先求(x,y).和例1一样,可用三种方法计算,只是柯 西-黎曼条件需改用极坐标形式.这里只介绍全微分显式法.其它 两种方法,请读者自行演算. 计算v的偏导数, 1 9那-√分in号, 按照柯西-黎曼方程(1.3.4),这是说, 2 -√号si 2 于是 du-dp+ag√cos号4p√台in号9 1 =√co√p+√Pco}=d2c罗}. 因此、 u=√2pcos号+C=√x+V+y+C, ±17