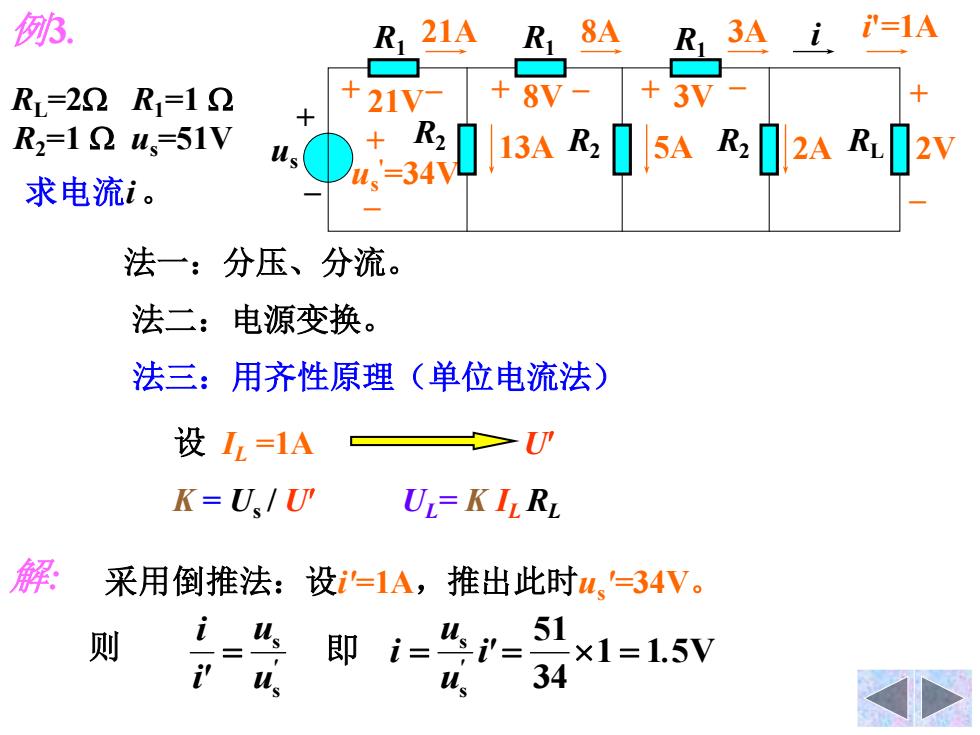
3. R1 21A R 8A R 3A i'=1A R=22R1=12 +21V- +8V-+3V R2=12u、=51V -系3AR小5AR2AR2y 求电流i。 法一:分压、分流。 法二: 电源变换。 法三:用齐性原理(单位电流法) 设I=1A >UU' K=U、/U' UL=K ILRL 解 采用倒推法:设'=1A,推出此时u、'=34V。 则 即 i=4= 51 ×1=1.5V us ls 34
例3. 解: 采用倒推法:设i'=1A,推出此时us '=34V。 则 求电流i 。 RL=2 R1=1 R2=1 us=51V R1 R1 R1 R2 R2 RL + – us i + – 13A 5A 2A 2V 21A 8A 3A + – + 21V– + 8V – 3V + – us '=34V R2 i'=1A 1 1 5V 34 51 s s s s i' . u u i u u i' i ' ' = 即 = = = 设 IL =1A 法一:分压、分流。 法二:电源变换。 法三:用齐性原理(单位电流法) U K = Us / U UL= K ILRL

可加性(additivity property) R 例4 us2 R R 线性 R 例5 ky ust k1r1+k22 k2 us2, R R k22. kus2 例6 usl kust kus2 kr. us R R 线性电路中,所有激励都增大(或减小)同样的倍数, 则电路中响应也增大(或减小)同样的倍数
可加性 (additivity property) 线性电路中,所有激励都增大(或减小)同样的倍数, 则电路中响应也增大(或减小)同样的倍数。 R us1 r1 R us2 r2 R k1 us1 k1 r1 R k2 us2 k2 r2 us1 us2 r R k us1 k us2 k r R 线性 例4 例5 例6 r1+ r2 us1 us2 R k2 us2 k1 r1+ k2 r2 R k1 us1

4.2替代定理(Substitution Theorem 替代定理:给定一个线性电阻电路,其中第k支路的电压u和电流i 为已知,那么此支路就可以用一个电压等于u的电压源u,或一个 电流等于的电流源1,替代,替代后电路中全部电压和电流均将保持 原值. 第 替代定理 k 或 N Wk N N 支路 us N:第k支路外的电路其余分 第k支路: 可以是电阻、电压源和电阻的串联组合或电流源和电阻 的并联组合。 如果第k支路中的电压或电流为N中受控源的控制量,而 替代后该电压或电流不复存在,则该支路不能被替代
替代定理: 给定一个线性电阻电路,其中第k支路的电压uk和电流ik 为已知,那么此支路就可以用一个电压等于uk的电压源us,或一个 电流等于ik的电流源i s替代,替代后电路中全部电压和电流均将保持 原值. 第 k 支 路 uk + _ N ik N:第k支路外的电路其余部分 uk + _ N ik + _ uS uk + _ N ik iS 或 第k支路:可以是电阻、电压源和电阻的串联组合或电流源和电阻 的并联组合。 如果第k支路中的电压或电流为N中受控源的控制量,而 替代后该电压或电流不复存在,则该支路不能被替代。 替代定理 4. 2 替代定理(Substitution Theorem)
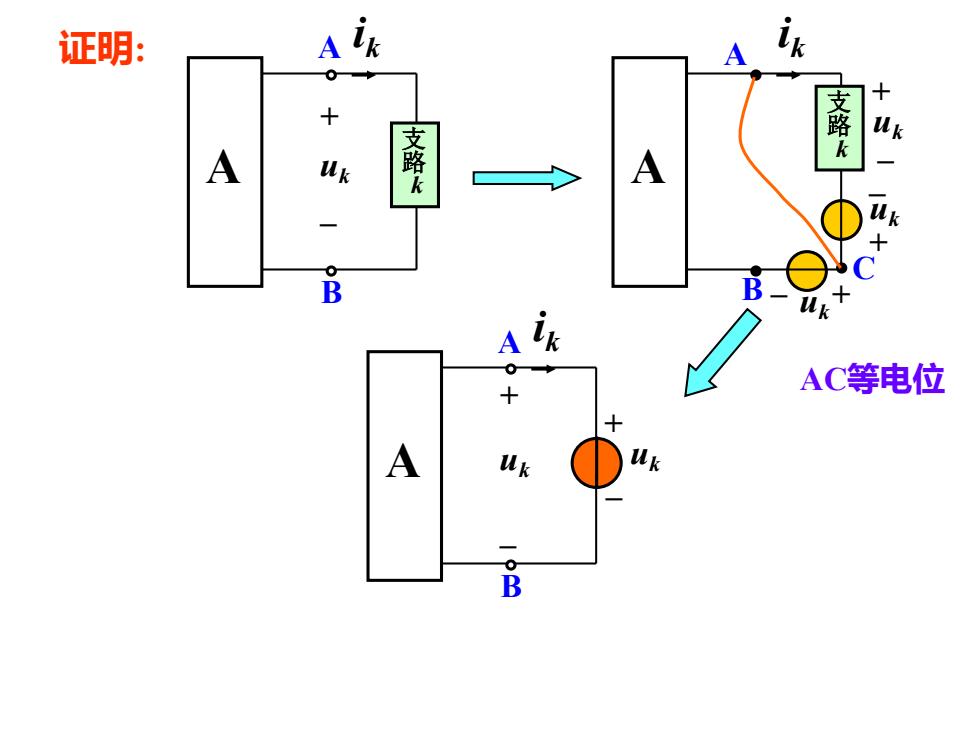
证明: A ik k 支路k 路k A A B AC等电位 A B
证明 : u k u k A ik +–uk 支路k – + +– A C B A ik +–u k 支路k AB AC等电位 +– A u k ik +–u k AB
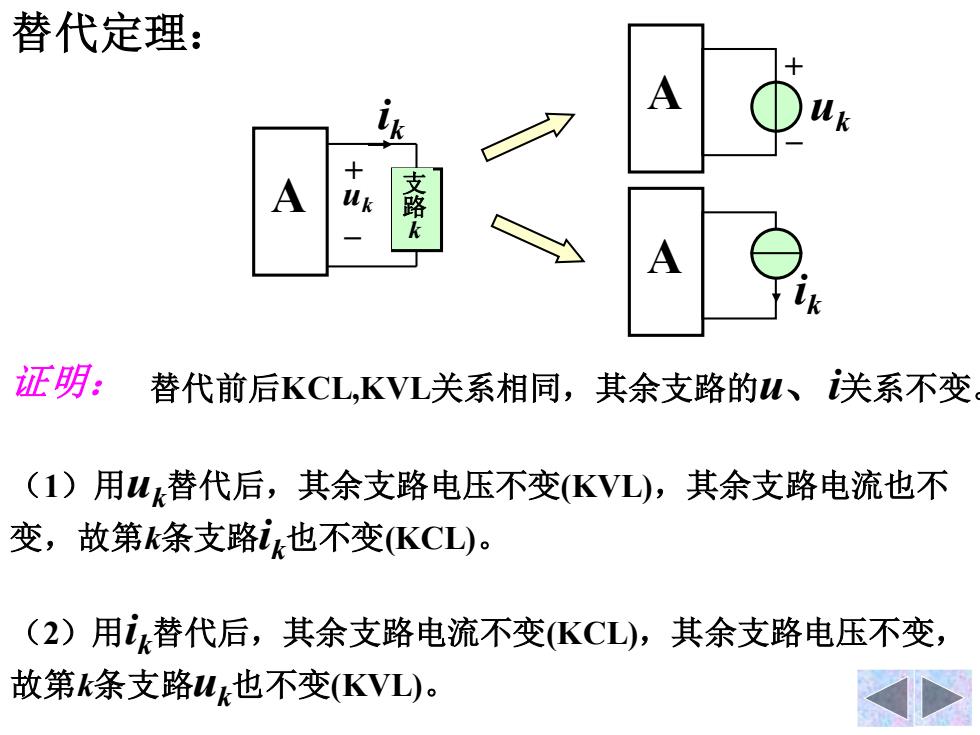
替代定理: A A Uk 支路k A 证明: 替代前后KCL,KVL关系相同,其余支路的u、关系不变 (1)用Wk替代后,其余支路电压不变(KVL),其余支路电流也不 变,故第k条支路k也不变(KCL)。 (2)用替代后,其余支路电流不变(KCL),其余支路电压不变, 故第k条支路W也不变(KVL)
替代定理: 证明: 替代前后KCL,KVL关系相同,其余支路的u、i关系不变。 (2)用ik替代后,其余支路电流不变(KCL),其余支路电压不变, 故第k条支路uk也不变(KVL)。 (1)用uk替代后,其余支路电压不变(KVL),其余支路电流也不 变,故第k条支路ik也不变(KCL)。 A ik + – uk 支 路 k A + – uk ik A