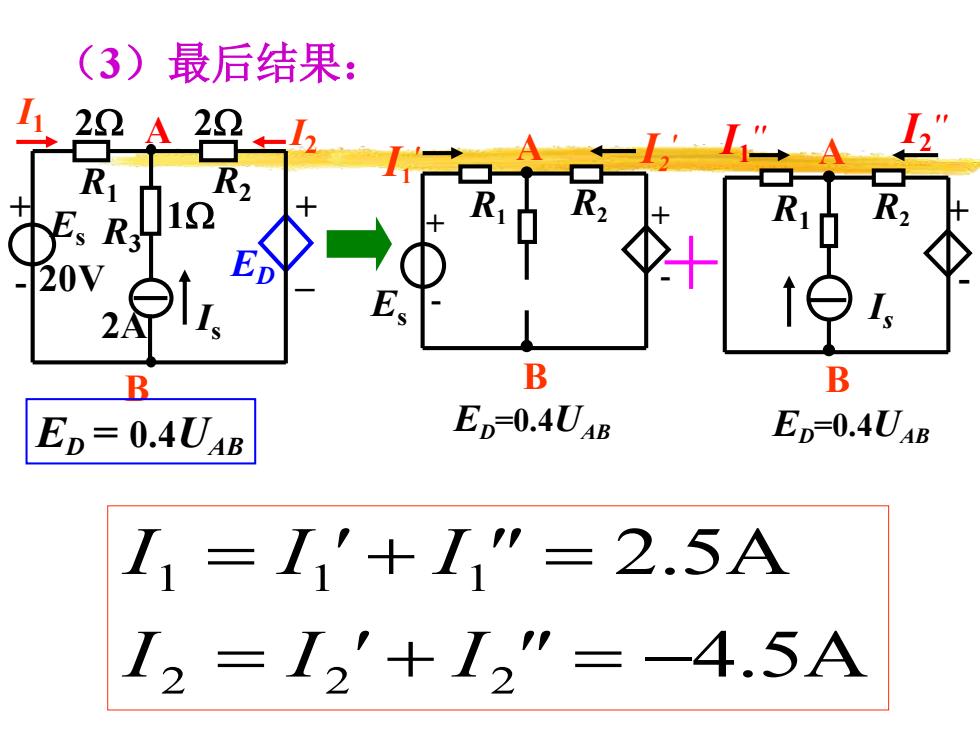
(3)最后结果: 22 A R Es R3 20V B B B ED=0.4UAB Ep=0.4UAB Ep=0.4UAB I1=I1'+I1"=2.5A 12=I2'+I2"=4.5A
(3)最后结果: 4.5A 2.5A 2 2 2 1 1 1 = + = − = + = I I ' I " I I ' I " Es + + - - R1 R2 A B ED=0.4UAB I1 ' I2 ' + - R1 R2 A B Is I2 '' I1 '' ED=0.4UAB + + - _ Es 20V R1 R3 R2 2A 2 2 1 Is A B I1 I2 ED ED = 0.4UAB
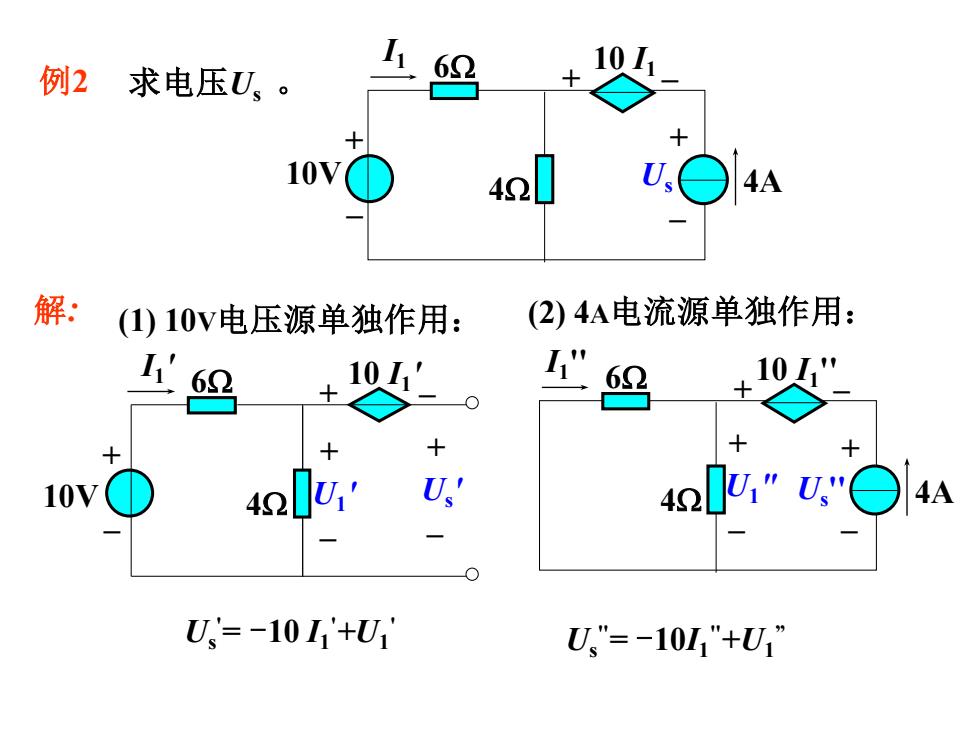
例2求电压U、。 62 10V 42L 4A 解: (1)10V电压源单独作用: (2)4A电流源单独作用: 10 " 10 42 U' U,' 42L U=-10I'+U1 U"=-101"+Ui
例2 求电压Us 。 解: (1) 10V电压源单独作用: (2) 4A电流源单独作用: + – 10V 6 I1 4A + – Us + – 10 I1 4 10V + – 6 I1 ' + – 10 I1 ' 4 + – Us ' 6 I1 '' 4A + – Us '' + – 10 I1 '' 4 + – U1 ' + – U1 " Us ' = -10 I1 '+U1 ' Us " = -10I1 "+U1
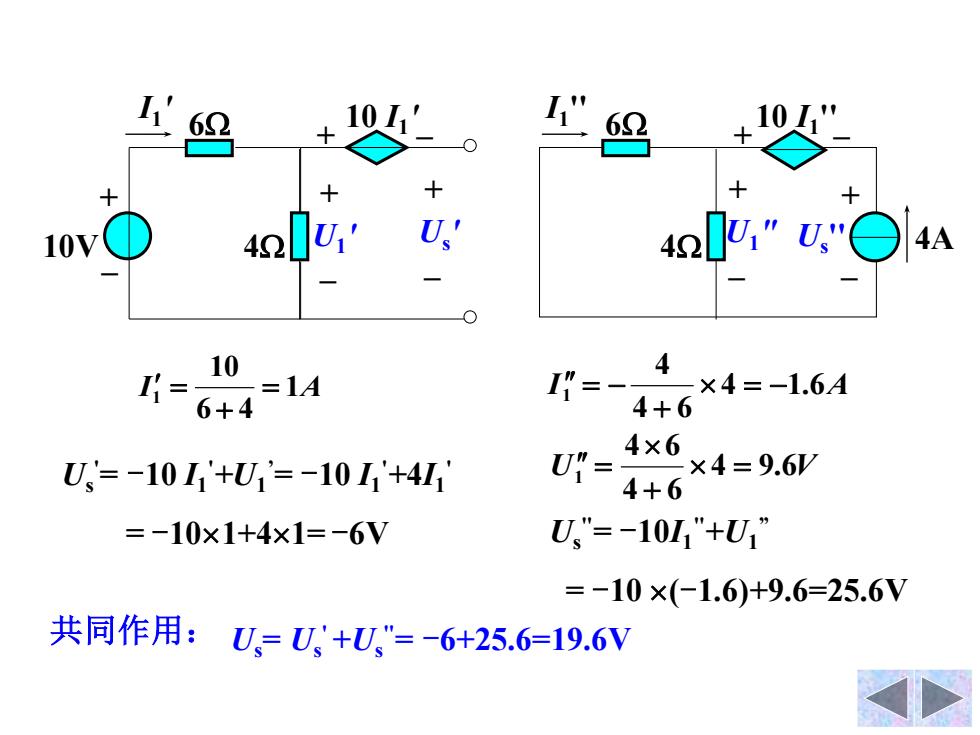
11 62 42 421 10 4 = =1A I=- ×4=-1.6A 6+4 4+6 U=-101'+U1'=-10I1'+4I1 Ui- 4×6 ×4=9.6V 4+6 =-10x1+4x1=-6V U"=-10M1"+U1” =-10×(-1.6)+9.6=25.6V 共同作用:Ug=U+U,"=-6+25.6=19.6V
Us ' = -10 I1 '+U1 ’ = -10 I1 '+4I1 ' = -101+41= -6V Us " = -10I1 "+U1 ” = -10 (-1.6)+9.6=25.6V 共同作用: Us= Us ' +Us " = -6+25.6=19.6V 10V + – 6 I1 ' + – 10 I1 ' 4 + – Us ' + – U1 ' 6 I1 '' 4A + – Us '' + – 10 I1 '' 4 + – U1 " I 1A 6 4 10 1 = + = I 4 1.6A 4 6 4 1 = − + = − U 4 9.6V 4 6 4 6 1 = + =
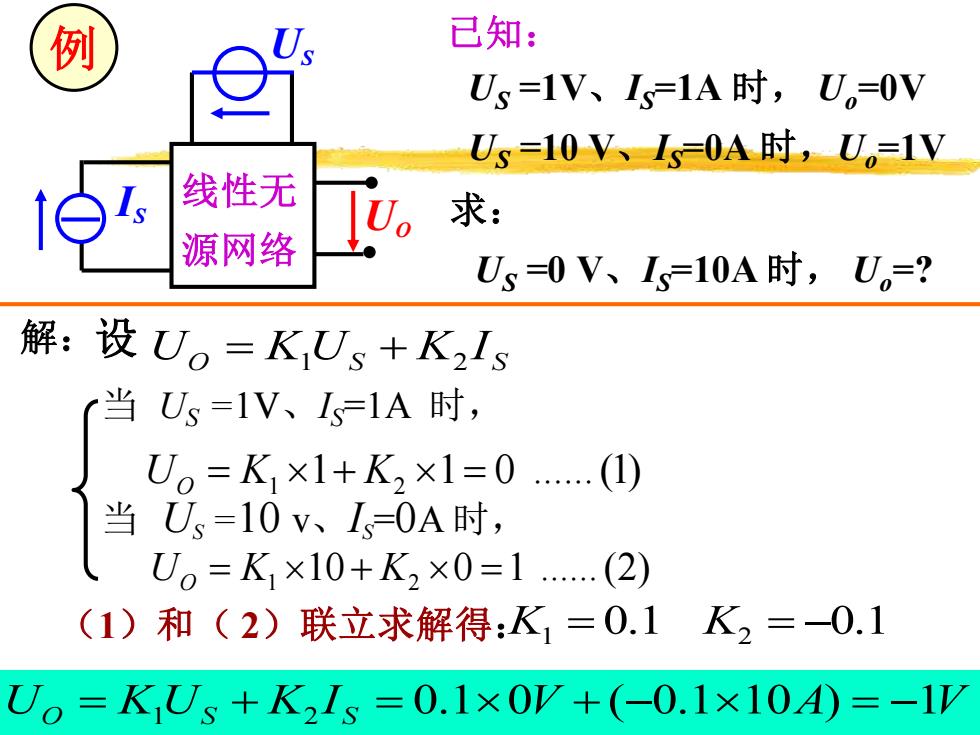
例 已知: Us=1V、Is=1A时,U。=0V Us=10V、I=0A时,U。=1V 线性无 求: 源网络 U Us=0V、I=10A时,U,=? 解:设U。=KUs+K2Is 当Us=1V、1s=1A时, U。=K×1+K2×1=0.(1) 当U=10v、I=0A时, Uo=K×10+K2×0=1.(2) (1)和(2)联立求解得:K1=0.1K2=0.1 Uo=KUs+K2Is=0.1×0V+(-0.1×10A)=-1/
例 US =1V、IS=1A 时, Uo=0V 已知: US =10 V、IS=0A 时,Uo=1V 求: US =0 V、IS=10A 时, Uo=? US 线性无 源网络 UO IS 解:设 O S S U K U K I = 1 + 2 (1)和( 2)联立求解得: K1 = 0.1 K2 = −0.1 当 US =1V、IS=1A 时, 1 1 0 .(1) UO = K1 + K2 = 当 US =10 v、IS =0A 时, 10 0 1 .(2) UO = K1 + K2 = UO = K1 US + K2 I S = 0.10V + (−0.110A) = −1V
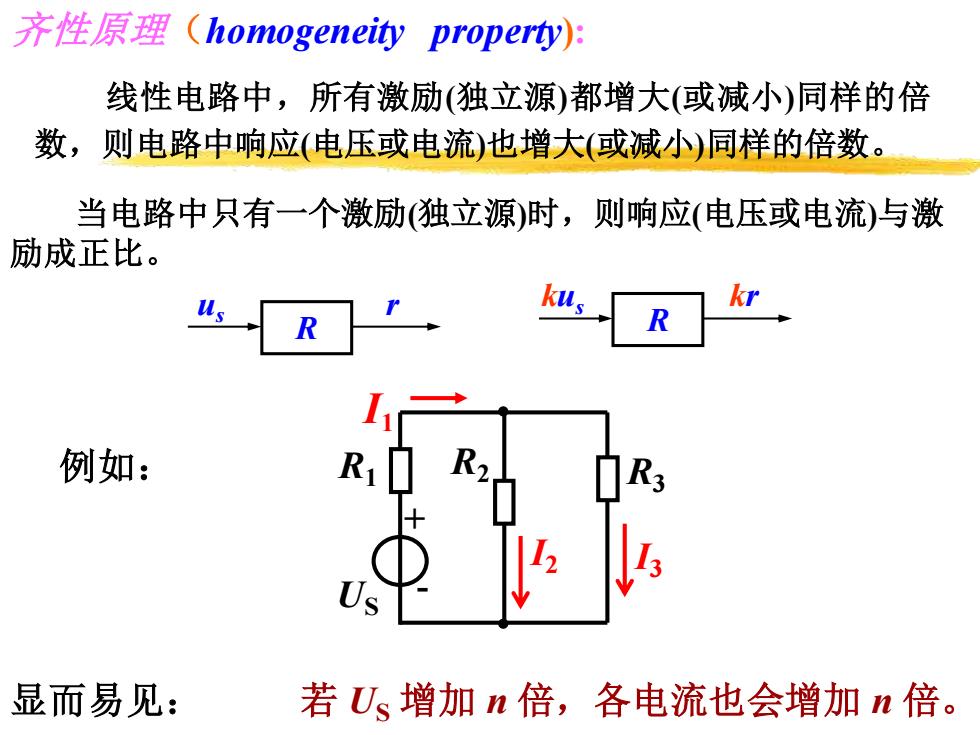
齐性原理(homogeneity property): 线性电路中,所有激励(独立源)都增大(或减小)同样的倍 数,则电路中响应(电压或电流)也增大(或减小)同样的倍数。 当电路中只有一个激励(独立源)时,则响应(电压或电流)与激 励成正比。 R 例如: R2. 显而易见: 若U增加n倍,各电流也会增加n倍
例如: R2 + U - S R3 I2 I3 R1 I1 显而易见: 若 US 增加 n 倍,各电流也会增加 n 倍。 齐性原理(homogeneity property): 线性电路中,所有激励(独立源)都增大(或减小)同样的倍 数,则电路中响应(电压或电流)也增大(或减小)同样的倍数。 当电路中只有一个激励(独立源)时,则响应(电压或电流)与激 励成正比。 R us r R kus kr