
i=i= R2 ust △ △ +Rug=t △ 或=1-6={ tRu Ru+R+R R+R24g △ △ △ =方+2+ =元=尽1队1+Rt尼L十尼,=话+6+写 △ △ △ 由上式可见,各支路电流均为各电压源的一次函数,所以 各支路电流(如)均可看成各电压源单独作用时,产生 的电流(如,i”,”)之叠加
' '' ''' u i i i R u R R u R i i s 3 1 1 1 1 2 s 2 1 2 2 2 s 1 2 2 1 a + = + + + = = − Δ Δ Δ ' '' ''' i i i u R R u R R R R u R R i i i 2 2 2 s 3 1 1 1 2 s 2 1 1 1 2 2 2 s 1 2 1 2 2 2 a b 1 = + + + + + + + − + = − = Δ Δ Δ ' '' ''' u i i i R u R R u R i i s 3 3 3 3 11 s 2 11 21 s 1 21 3 b = + + − + + + − = = Δ Δ Δ 各支路电流(如i1)均可看成各电压源单独作用时,产生 的电流(如i1 ' ,i1 " ,i1 "')之叠加。 由上式可见, 各支路电流均为各电压源的一次函数,所以

当一个电源单独作用时,其余电源不作用,就意味着取零 值。即对电压源看作短路,而对电流源看作开路。即如下图: 3 一3' R3 三个电源共同作用 Ws单独作用 3" R3 R 山、2单独作用 + 山s3单独作用
当一个电源单独作用时,其余电源不作用,就意味着取零 值。即对电压源看作短路,而对电流源看作开路。 三个电源共同作用 = = us1单独作用 + us2单独作用 + + us3单独作用 + 即如下图: R1 us1 R2 us2 R3 us3 i1 i2 i3 + – + – + – ia ib R1 us1 R2 R3 i1 ' i2 ' i3 ' + – R1 R2 us2 R3 i1 '' i2 '' i3 '' + – R1 R2 R3 us3 i1 ''' i2 ''' i3 ''' + –
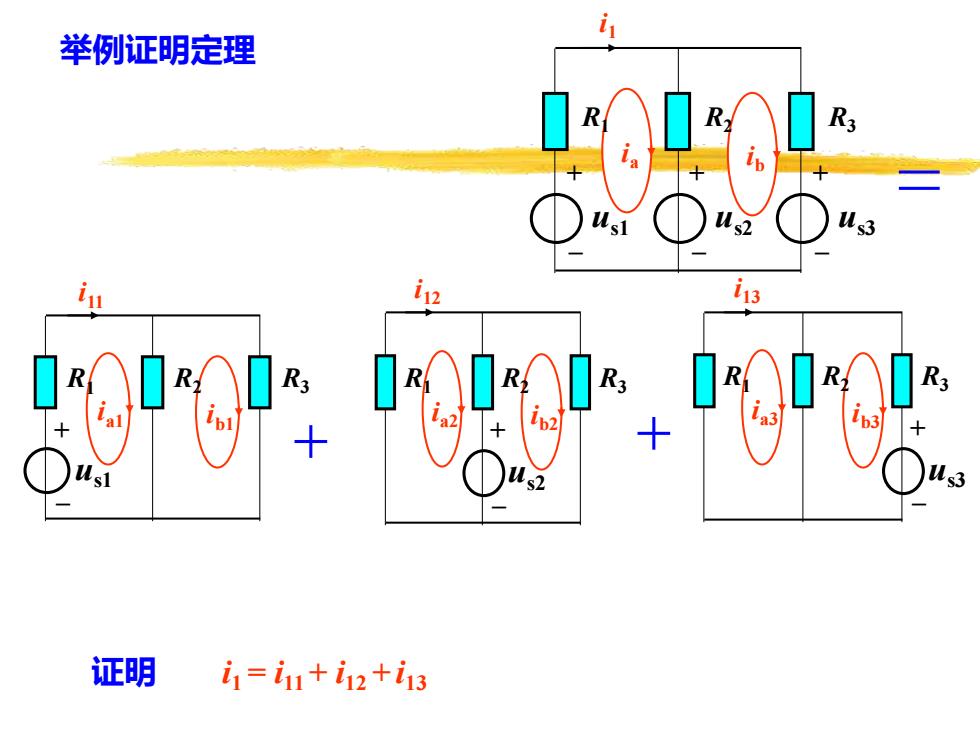
i 举例证明定理 113 1a2 证明 i1=i11+i12+i13
举例证明定理 ib1 ia1 R1 R2 R3 + – us1 i11 ib ia R2 + – R3 + – R1 + – us1 us2 us3 i1 ib2 ia2 R2 + – R1 R3 us2 i12 ib3 ia3 R2 R3 + – R1 us3 i13 i1 = i11 + i12 + i 证明 13
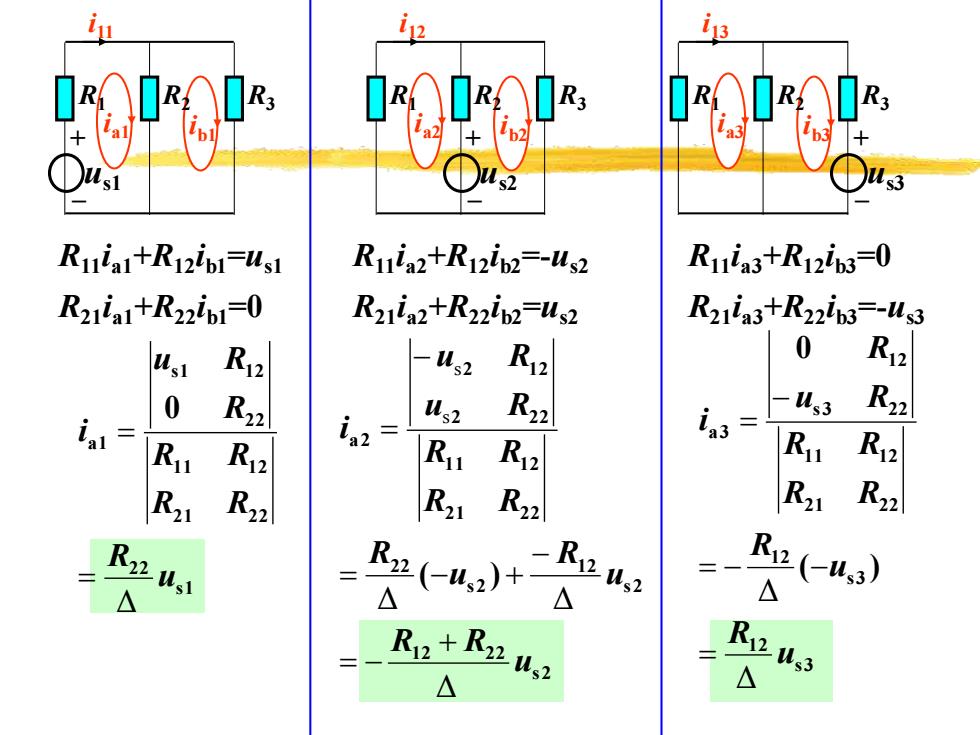
IOIROR b3 Ruiat+Rizipl=ust Ruia2+R12in2=-us2 R11a3+R12b3=0 Rziial+R22ipI=0 Rzia2+R22i2=us2 R21ia3+R22ib3=-us3 ust R12 -Us2 Ri2 0 R12 0 R22 us2 R22 in3 -Us3 R22 R12 R R12 R R2 R2 R22 R21 R22 R21 R22 R业1 △ (-,2)+ △ △ △ z+Riu? Ryus △ △
ib1 ia1 R1 R2 R3 + – us1 i11 ib2 ia2 R2 + – R1 R3 us2 i12 ib3 ia3 R2 R3 + – R1 us3 i13 R11ia1+R12ib1=us1 R21ia1+R22ib1=0 R11ia2+R12ib2=-us2 R21ia2+R22ib2=us2 R11ia3+R12ib3=0 R21ia3+R22ib3=-us3 Δ s1 22 21 22 11 12 22 s1 12 a1 0 u R R R R R R u R i = = Δ Δ Δ s s s2 12 22 s2 12 s2 22 21 22 11 12 2 22 2 12 a2 ( ) u R R u R u R R R R R u R u R i + = − − = − + − = Δ Δ s3 12 s3 12 21 22 11 12 s3 22 12 a3 ( ) 0 u R u R R R R R u R R i = = − − − =
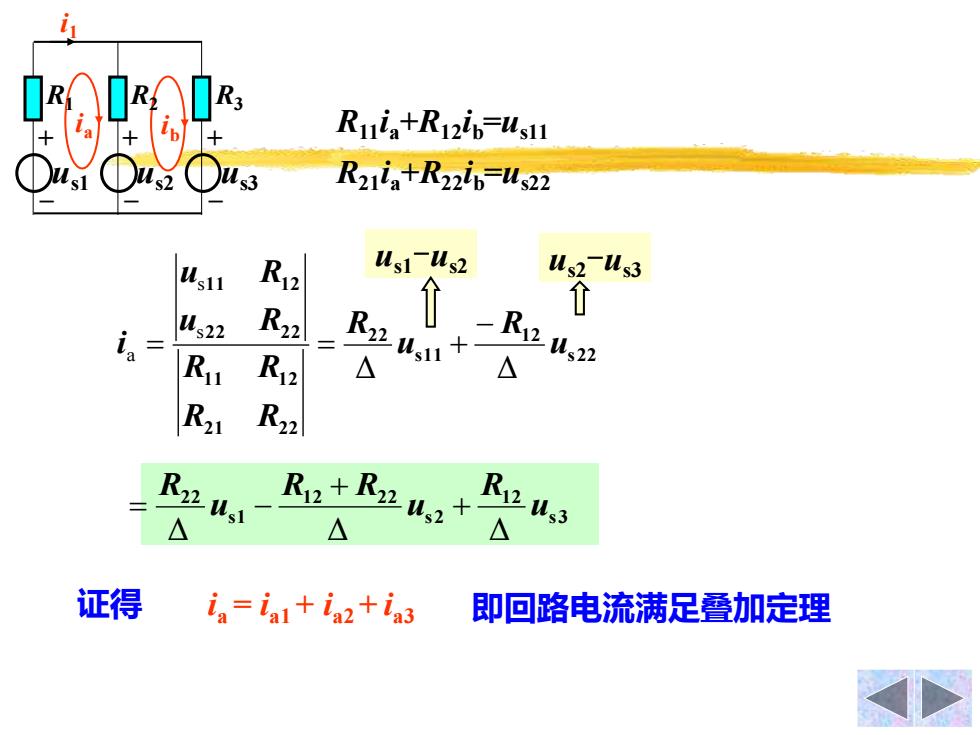
Ruia+Rizip-usu 3 Rzia+Rzip-us22 R12 us1-儿s2 us2 Us3 个 i= Us22 R22 Ru Ri2 △ △ R21 R22 △ R2+R2W,+ △ Rzus3 △ 证得 ia=ia+in2+ia3 即回路电流满足叠加定理
ib ia R2 + – R3 + – R1 + – us1 us2 us3 i1 R11ia+R12ib =us11 R21ia+R22ib =us22 Δ Δ s s a s2 2 1 2 s1 1 2 2 2 1 2 2 1 1 1 2 2 2 2 2 1 1 1 2 u R u R R R R R u R u R i − = = + s3 1 2 s2 1 2 2 2 s1 2 2 u R u R R u R Δ Δ Δ + + = − us1-us2 us2-us3 ia = ia1 + ia2 + i 证得 a3 即回路电流满足叠加定理