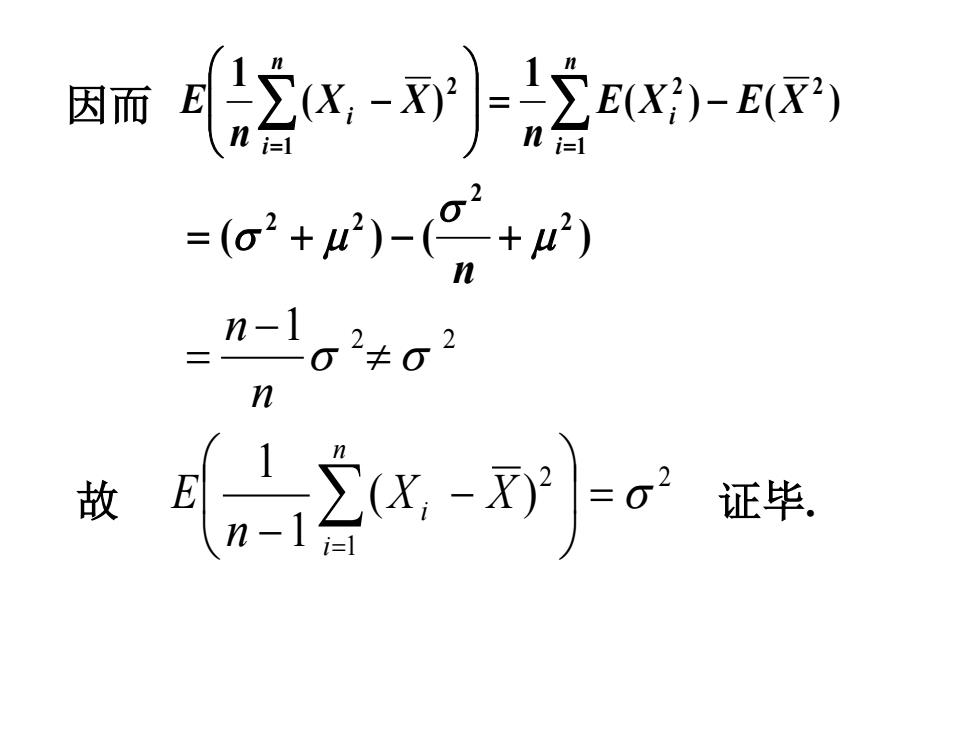
因而2x-W24- =(a2+)-g+2) =n-1g2 故 cn2-wj。 证毕
( ) ( ) 1 ( ) 1 2 1 2 1 2 E X E X n X X n E n i i n i i = − ∑ − ∑ = = 因而 ( ) ( ) 2 2 2 2 µ σ = σ + µ − + n 1 2 2 σ ≠ σ − = n n 2 1 2 ( ) 1 1 = σ − − ∑ = n i Xi X n 故 E 证毕

例3设X1,X2,,Xm)是总体X的一个样本, X~B(n,p)n>1,求p2的无偏估计量. 解由于样本矩是总体矩的无偏估计量以及 数学期望的线性性质,只要将未知参数表示成 总体矩的线性函数,然后用样本矩作为总体矩 的估计量,这样得到的未知参数的估计量即为 无偏估计量. 令X=E(X)=np 1x?=E(X2)=(np)2+p(1-p) m i=l
例3 设( , , , ) X1 X2 X m 是总体 X 的一个样本 , X ~ B ( n , p ) n > 1 , 求 p 2 的无偏估计量. 解 由于样本矩是总体矩的无偏估计量以及 数学期望的线性性质, 只要将未知参数表示成 总体矩的线性函数, 然后用样本矩作为总体矩 的估计量, 这样得到的未知参数的估计量即为 无偏估计量. 令 X = E(X ) = np ( ) ( ) (1 ) 1 2 2 1 2 X E X np np p m m i ∑ i = = + − =
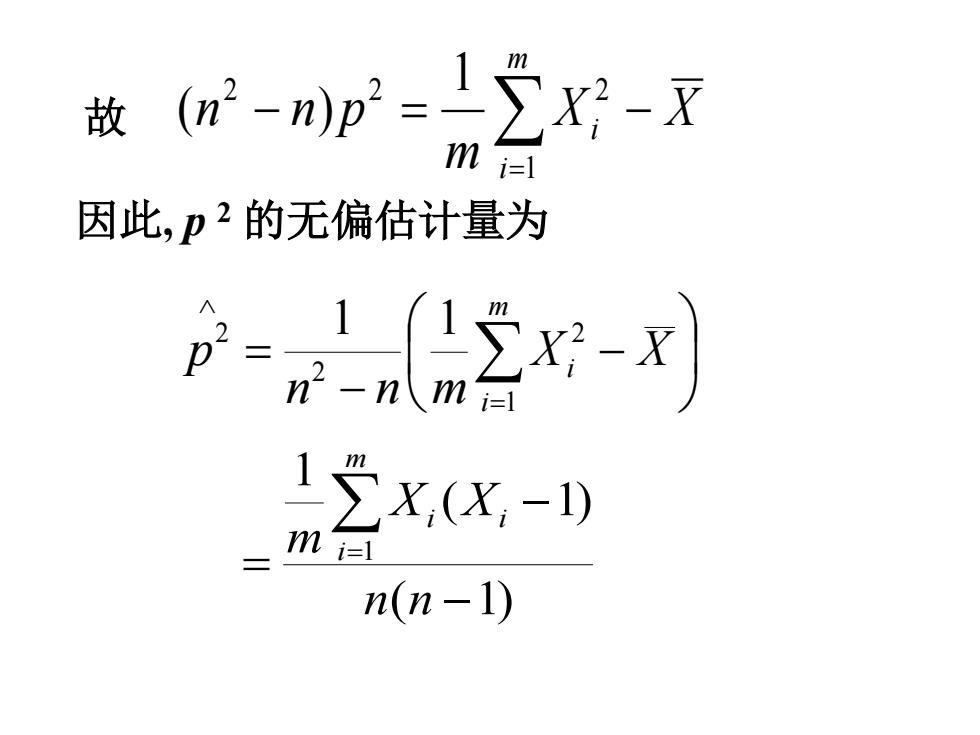
故m2-mp2=12x-X m i=1 因此,p2的无偏估计量为 p-eΣ-了 12X,(X,-1) m i=l n(n-1)
− − = ∑ = ∧ X X n n m p m i i 1 2 2 2 1 1 因此, p 2 的无偏估计量为 ( 1) ( 1) 1 1 − − = ∑ = n n X X m m i i i 故 X X m n n p m i − = ∑ i − =1 2 2 1 2 ( )