
40 Ly() (w) L1() Ls(o) (e) (a) (V) 90 () () ()h(@) 90 〔 () -180 (b) (Vs) 图5-9例5一1的伯德图 绘制开环对数相频特性曲线时,先作出各环节的相频特性曲线?,()一 p,(0),然后进行代数相加,如图5一9b)所示的0(o). 由上述例题可见,串联环节的对数幅频特性也可以直接绘出。从典型环节的对 数幅频特性可见,在低频段,惯性、振荡和比例微分等环节的低频渐近线,均为零 分贝线。因此,对数幅频特性L()的低频段主要取决于比例环节和积分环节(理想 微分环节一般很少出现)。而在0=1处,积分环节为过零点,因此在⊙=1处,对 数幅频特性的高度仅取决于比例环节。即L(⊙以=20gK,此时的斜率,则主 要取决于积分环节的多少,每多一个积分环节,则斜率便降低一20dB/dcc。若有V 个积分环节,则在0=1处的斜率便为一20VdB/dec。在确定了低频段以后,往后 0
70 图 5-9 例 5—1 的伯德图 绘制开环对数相频特性曲线时,先作出各环节的相频特性曲线 (1 )一 (5 ) ,然后进行代数相加,如图 5—9(b)所示的 ()。 由上述例题可见,串联环节的对数幅频特性也可以直接绘出。从典型环节的对 数幅频特性可见,在低频段,惯性、振荡和比例微分等环节的低频渐近线,均为零 分贝线。因此,对数幅频特性 L() 的低频段主要取决于比例环节和积分环节(理想 微分环节一般很少出现)。而在 =1 处,积分环节为过零点,因此在 =1 处,对 数幅频特性的高度仅取决于比例环节。即 L() =1 = 20lg K ,此时的斜率,则主 要取决于积分环节的多少,每多一个积分环节,则斜率便降低—20dB/dec。若有 V 个积分环节,则在 =1 处的斜率便为—20VdB/dec。在确定了低频段以后,往后

若遇到一阶惯性环节,经交接频率,L(o)的斜率便降低一20dB/dec:遇到二阶振 荡环节,过交接频率,则斜率便降低一40dB/dec:若遇到比例微分环节,过交接频 率,则斜率增加+20dB/dec。这样,掌握了以上规律,就可以直接画出串联环节的 总的渐近对数幅频特性。其步骤是: ①分析系统是由哪些典型环节串联组成的,将这些典型环节的传递函数都化 成标准形式。即各典型环节传递函数的常数项为1。 ②根据比例环节的K值,计算20gK。 ③在半对数坐标纸上,找到横坐标为0=1、纵坐标为L(四a=20gK的 点,过该点作斜率为一20VdB/dec的斜线,其中V为积分环节的数目。 ④计算各典型环节的转角频率,将各转角频率按由低到高的顺序进行排列, 并按下列原则依次改变L(o)的斜率: 若过一阶惯性环节的转角频率,斜率减去20dB/dec: 若过比例微分环节的转角频率,斜率增加20dB/dec: 若过二阶振荡环节的转角频率,斜率减去40dB/dec。 如果需要,可对渐近线进行修正,以获得较精确的对数幅频特性曲线。 例5一2引绘出开环传递函数为 G(s)= 5(s+2) s(s+1)0.05s+1) 的系统开环对数频率特性。 解:将G(s)中的各因式换成典型环节的标准形式,即 G(s)= 10(0.5s+1) s(s+1)(0.05s+1) 如果直接绘制系统开环对数幅频特性渐近线,其步骤如下: (1)转折频率01=1,02=2,03=20。 (2)在0=1处,L(o。1=20gK=20lg10=20dB. 之
71 若遇到一阶惯性环节,经交接频率, L() 的斜率便降低—20dB/dec;遇到二阶振 荡环节,过交接频率,则斜率便降低—40dB/dec;若遇到比例微分环节,过交接频 率,则斜率增加+20dB/dec。这样,掌握了以上规律,就可以直接画出串联环节的 总的渐近对数幅频特性。其步骤是: ① 分析系统是由哪些典型环节串联组成的,将这些典型环节的传递函数都化 成标准形式。即各典型环节传递函数的常数项为 1。 ② 根据比例环节的 K 值,计算 20lg K 。 ③ 在半对数坐标纸上,找到横坐标为 =1、纵坐标为 L() =1 = 20lg K 的 点,过该点作斜率为—20VdB/dec 的斜线,其中 V 为积分环节的数目。 ④ 计算各典型环节的转角频率,将各转角频率按由低到高的顺序进行排列, 并按下列原则依次改变 L() 的斜率: 若过一阶惯性环节的转角频率,斜率减去 20dB/dec; 若过比例微分环节的转角频率,斜率增加 20dB/dec; 若过二阶振荡环节的转角频率,斜率减去 40dB/dec。 ⑤ 如果需要,可对渐近线进行修正,以获得较精确的对数幅频特性曲线。 [例 5—2] 绘出开环传递函数为 ( 1)(0.05 1) 5( 2) ( ) + + + = s s s s G s 的系统开环对数频率特性。 解:将 G(s) 中的各因式换成典型环节的标准形式,即 ( 1)(0.05 1) 10(0.5 1) ( ) + + + = s s s s G s 如果直接绘制系统开环对数幅频特性渐近线,其步骤如下: (1)转折频率 1 =1,2 =2,3=20。 (2)在 =l 处, L() =1 = 20lg K = 20lg10 = 20dB
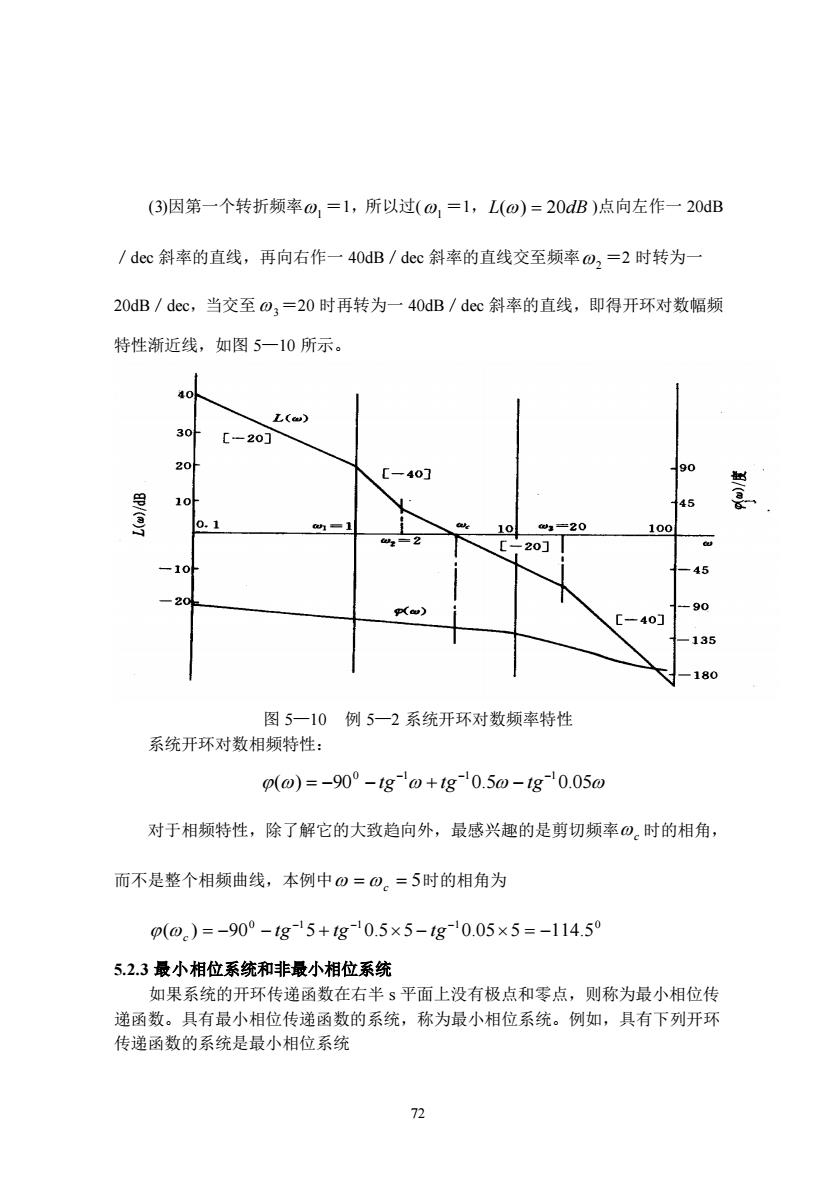
(3)因第一个转折频率o,=1,所以过(o,=1,L(o)=20dB)点向左作一20B /dcc斜率的直线,再向右作一40dB/dec斜率的直线交至频率o,=2时转为一 20dB/dec,当交至0,=20时再转为一40dB/dec斜率的直线,即得开环对数幅频 特性渐近线,如图5一10所示。 35 图5一10例5一2系统开环对数频率特性 系统开环对数相频特性: p(o)=-90°-tgo+tg10.50-1g10.050 对于相频特性,除了解它的大致趋向外,最感兴趣的是剪切频率⊙。时的相角, 而不是整个相频曲线,本例中0=0。=5时的相角为 p(0.)=-90°-g15+g10.5×5-g10.05×5=-114.59 5.2.3最小相位系统和非最小相位系统 如果系统的开环传递函数在右半s平面上没有极点和零点,则称为最小相位传 递函数。具有最小相位传递函数的系统,称为最小相位系统。例如,具有下列开环 传递函数的系统是最小相位系统
72 (3)因第一个转折频率 1 =1,所以过( 1 =1,L() = 20dB )点向左作一 20dB /dec 斜率的直线,再向右作一 40dB/dec 斜率的直线交至频率 2 =2 时转为一 20dB/dec,当交至 3=20 时再转为一 40dB/dec 斜率的直线,即得开环对数幅频 特性渐近线,如图 5—10 所示。 图 5—10 例 5—2 系统开环对数频率特性 系统开环对数相频特性: () 90 0.5 0.05 0 −1 −1 −1 = − − tg + tg − tg 对于相频特性,除了解它的大致趋向外,最感兴趣的是剪切频率 c 时的相角, 而不是整个相频曲线,本例中 =c = 5 时的相角为 0 1 1 1 0 ( ) = −90 − 5 + 0.55 − 0.055 = −114.5 − − − c tg tg tg 5.2.3 最小相位系统和非最小相位系统 如果系统的开环传递函数在右半 s 平面上没有极点和零点,则称为最小相位传 递函数。具有最小相位传递函数的系统,称为最小相位系统。例如,具有下列开环 传递函数的系统是最小相位系统

K(Ts+1) G,()=(gs+IXTs+D (K,T,T2,T3均为正数) 开环传递函数在右半s平面上有一个或多个)极点和零点,称为非最小相位传 递函数(若开环传递函数有一个或多个极点位于右半;平面,这意味着开环不稳定) 具有非最小相位传递函数的系统称为非最小相位系统。例如,具有下列开环传递函 数的系统为非最小相位系统 K(Ts-1) G(s)= (K,T,T2,T均为正数) (Ts+1X(Ts+1) K G()sD" (K,T,T2,x均为正数) G,(S)和G2()都具有相同的幅频特性,即幅频特性都是 K1+To2 M(o)= 0+T2o21+T2o2) 但它们的相频特性却大大不同:设G,(s)和G,(s)的相频特性分别为口,(o)和 p2(),则 p,(@)=g'(To)-g(To)-g'(T,o) 0,o=g9-g口o)-gg, 当0=0时 p,(o)=0°,p2()=180° 当0→∞时 9,(∞)=90°-90°-90°=-909 p,(0)=90°-90°-90°=-90 对于最小相位系统G,(s)来说,当0从0一∞时的相角变化为 l0(∞)-m,(0=90°-0|=90% 73
73 ( 1)( 1) ( 1) ( ) 1 2 3 1 + + + = T s T s K T s G s ( 1 2 3 K,T ,T ,T 均为正数) 开环传递函数在右半 s 平面上有一个(或多个) 极点和零点,称为非最小相位传 递函数(若开环传递函数有一个或多个极点位于右半 s 平面,这意味着开环不稳定)。 具有非最小相位传递函数的系统称为非最小相位系统。例如,具有下列开环传递函 数的系统为非最小相位系统 ( 1)( 1) ( 1) ( ) 1 2 3 2 + + − = T s T s K T s G s ( 1 2 3 K,T ,T ,T 均为正数) s e T s T s K G s − + + = ( 1)( 1) ( ) 1 2 3 ( , , , K T1 T2 均为正数) ( ) 1 G s 和 ( ) 2 G s 都具有相同的幅频特性,即幅频特性都是 (1 )(1 ) 1 ( ) 2 2 2 2 2 1 2 2 3 T T K T M + + + = 但它们的相频特性却大大不同;设 ( ) 1 G s 和 ( ) 2 G s 的相频特性分别为 ( ) 1 和 ( ) 2 , 则 ) ( ) ( ) 1 ( ) ( ( ) ( ) ( ) ( ) 2 1 1 1 3 1 2 2 1 1 1 3 1 1 tg T tg T T tg tg T tg T tg T − − − − − − − − − = = − − 当 =0 时 0 2 0 1 () = 0 , () =180 当 →∞时 0 0 0 0 2 0 0 0 0 1 ( ) 90 90 90 90 ( ) 90 90 90 90 = − − = − = − − = − 对于最小相位系统 ( ) 1 G s 来说,当 从 0→∞时的相角变化为 0 0 0 1 () −1 (0) = − 90 − 0 = 90

对于非最小相位系统G,(s)来说,当0从0一∞时的相角变化为 p2(o)-p2(0y=90°-180|=270 显然,最小相位系统的相角变化为最小。 自动控制系统中迟延环节是最常见的非最小相位传递函数。例如上述的G(S) 包含了延迟环节e·。当延迟时间x比较小的时候,ea可近似为 es≈1-石(泰勒级数展开取前两项) 因此,对G,(s)而言,延迟环节若按上式近似,则G,(s)= K(1-s) (Ts+10(T2s+1D 3(@)=1g(-ro)-1g(T@)-1g-(T@) 当0=0时 p(@)=0 当0→∞时 p,(∞)=-90°-90°-90°=-270° 当0从0一∞时,相角变化为 1p,(∞)-p,0=-270°-0|=270 所以它具有非最小相位系统的特性。如果要对G,(S)求取精确的相角变化,则 可对G(S)求取相频特性p,(o) p(⊙)=-gT0-gT0-57.3t0 当0=0时 03(0)=0° 当0→∞时p,()=-90°-90°-57.3.0=-0 由此得相角变化为 p3(o)-p3(0=0
74 对于非最小相位系统 ( ) 2 G s 来说,当 从 0→∞时的相角变化为 0 0 0 2 () − 2 (0) = − 90 −180 = 270 显然,最小相位系统的相角变化为最小。 自动控制系统中迟延环节是最常见的非最小相位传递函数。例如上述的 ( ) 3 G s 包含了延迟环节 s e − 。当延迟时间 比较小的时候, s e − 可近似为 e s s − − 1 (泰勒级数展开取前两项) 因此,对 ( ) 3 G s 而言,延迟环节若按上式近似,则 ( 1)( 1) (1 ) ( ) 1 2 3 + + − = T s T s K s G s ( ) ( ) ( ) ( ) 2 1 1 1 1 3 tg tg T tg T − − − = − − − 当 =0 时 0 3 () = 0 当 →∞时 0 0 0 0 3 () = −90 − 90 − 90 = −270 当 从 0→∞时,相角变化为 0 0 0 3 () − 3 (0) = − 270 − 0 = 270 所以它具有非最小相位系统的特性。如果要对 ( ) 3 G s 求取精确的相角变化,则 可对 ( ) 3 G s 求取相频特性 ( ) 3 = − − − − − ( ) 2 57.3 1 1 1 3 tg T tg T 当 =0 时 0 3 (0) = 0 当 →∞时 () = −90 − 90 − 57.3 = − 0 0 3 由此得相角变化为 3 () −3 (0) =