新疆大学：《自动控制理论》课程教学资源（教案讲义）第五章 频率响应法

4.二阶振荡环节 02 32+255+0) 和二阶微分环节(52+250s+o) 二阶环节中参数5（阻尼比）如果大于1，则可用两个一阶惯性环节 *1和 万9中的乘积来表示。或两个一阶微分环节5+1和5+1的桑积来表示。如 1 果0<5<1，则成为二阶振荡环节或二阶微分环节。由于二阶振荡环节和二阶微分 环节互为倒数（只相差一常数®）。所以只要讨论其中的一个，就可以方便地得到另 一个的对数幅频特性和相频特性（如上两小节的积分环节对微分环节，一阶惯性环节 对比例微分环节，只要画出对称于0轴的伯德图即可)。现着重讨论常见的二阶振荡 02 环节 的伯德图的绘制方法。 s2+250ns+01 二阶振荡环节的幅相频率特性为 G(j@)- 250 式中 p(@)=-1g 所以，二阶振荡环节的对数幅频特性和相频特性为 65

65 4．二阶振荡环节         + + 2 2 2 2 n n s  s   和二阶微分环节 ( ) 2 2 2 n n s +  s + 二阶环节中参数  (阻尼比)如果大于 l，则可用两个一阶惯性环节 1 1 T1 s + 和 1 1 T2 s + 的乘积来表示。或两个一阶微分环节 T1 s +1 和 T2 s +1 的乘积来表示。如 果 0＜  ＜1，则成为二阶振荡环节或二阶微分环节。由于二阶振荡环节和二阶微分 环节互为倒数(只相差一常数 2  n )。所以只要讨论其中的一个，就可以方便地得到另 一个的对数幅频特性和相频特性(如上两小节的积分环节对微分环节，一阶惯性环节 对比例微分环节，只要画出对称于  轴的伯德图即可)。现着重讨论常见的二阶振荡 环节         + + 2 2 2 2 n n s  s   的伯德图的绘制方法。 二阶振荡环节的幅相频率特性为 ( ) 2 2 2 2 2 1 2 1 2 1 1 ( )              j n n n n e j j G j         +         − = +        +         = 式中                       − = − − 2 1 1 2 ( ) n n tg        所以，二阶振荡环节的对数幅频特性和相频特性为

uo-e-gg】 250 p(0)=-g 依照一阶惯性环节的方法，先求出二阶振荡环节的对数幅频特性的渐近线 (1)当0<<0时，（低频段），L(o)≈-20g1=0(dB) 上式表明，低频段的渐近线为一条零分贝的直线，它与轴重合。 (②)当0>0，时，（高频段），L(o)≈-20g包=-40g2 0n 上式表明，高频段的渐近线为一条斜率为一40(dB/dec)的直线，它与o轴相交 于0=0n的点。 以上两条低频段和高频段的渐近线相交处频率0=0，称为二阶振荡环节的转 角频率，两条渐近线与转角频率如图5一6(a)所示。 图5一6二阶报荡环节，+20+@的伯德图

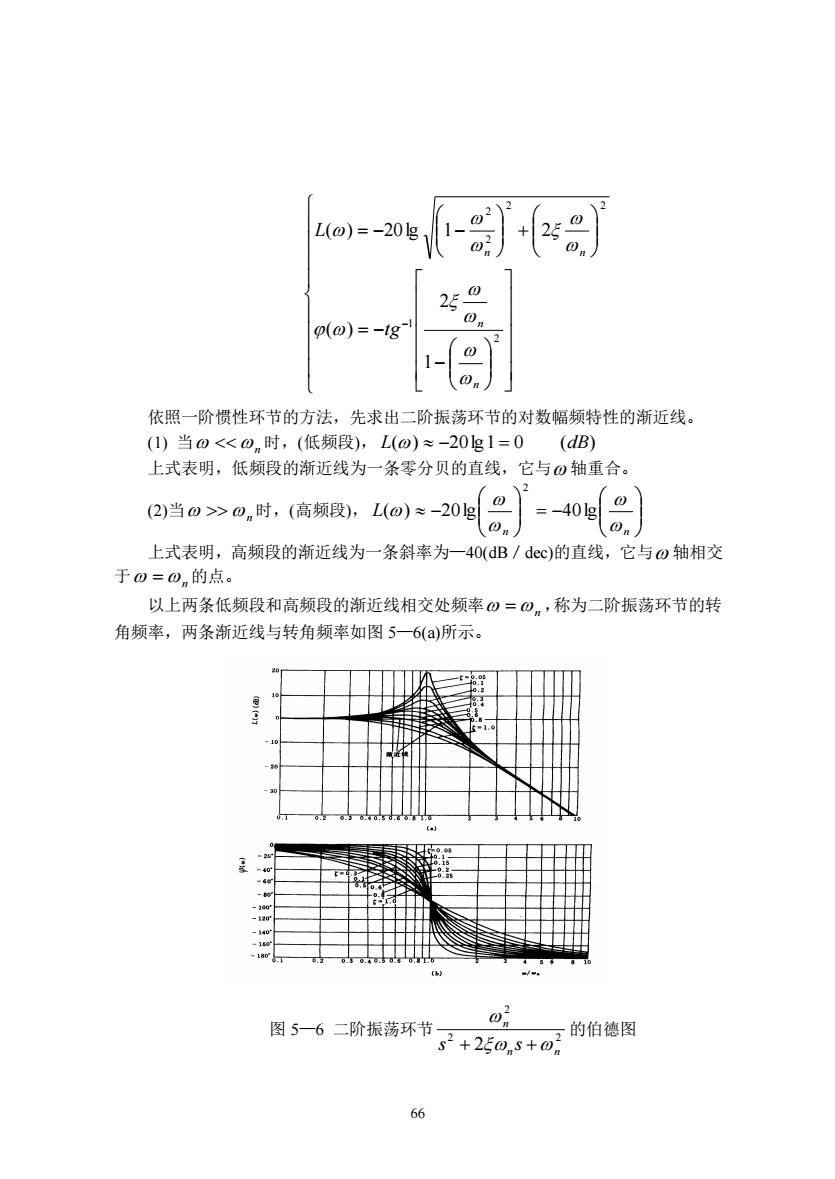
66                                  − = −         +         = − − − 2 1 2 2 2 2 1 2 ( ) ( ) 20lg 1 2 n n n n tg L              依照一阶惯性环节的方法，先求出二阶振荡环节的对数幅频特性的渐近线。 (1) 当   n 时，(低频段)， L()  −20lg1 = 0 (dB) 上式表明，低频段的渐近线为一条零分贝的直线，它与  轴重合。 (2)当   n 时，(高频段)，         = −          − n n L     () 20lg 40lg 2 上式表明，高频段的渐近线为一条斜率为—40(dB／dec)的直线，它与  轴相交 于  =n 的点。 以上两条低频段和高频段的渐近线相交处频率  =n ，称为二阶振荡环节的转 角频率，两条渐近线与转角频率如图 5—6(a)所示。 图 5—6 二阶振荡环节 2 2 2 2 n n n s  s   + + 的伯德图

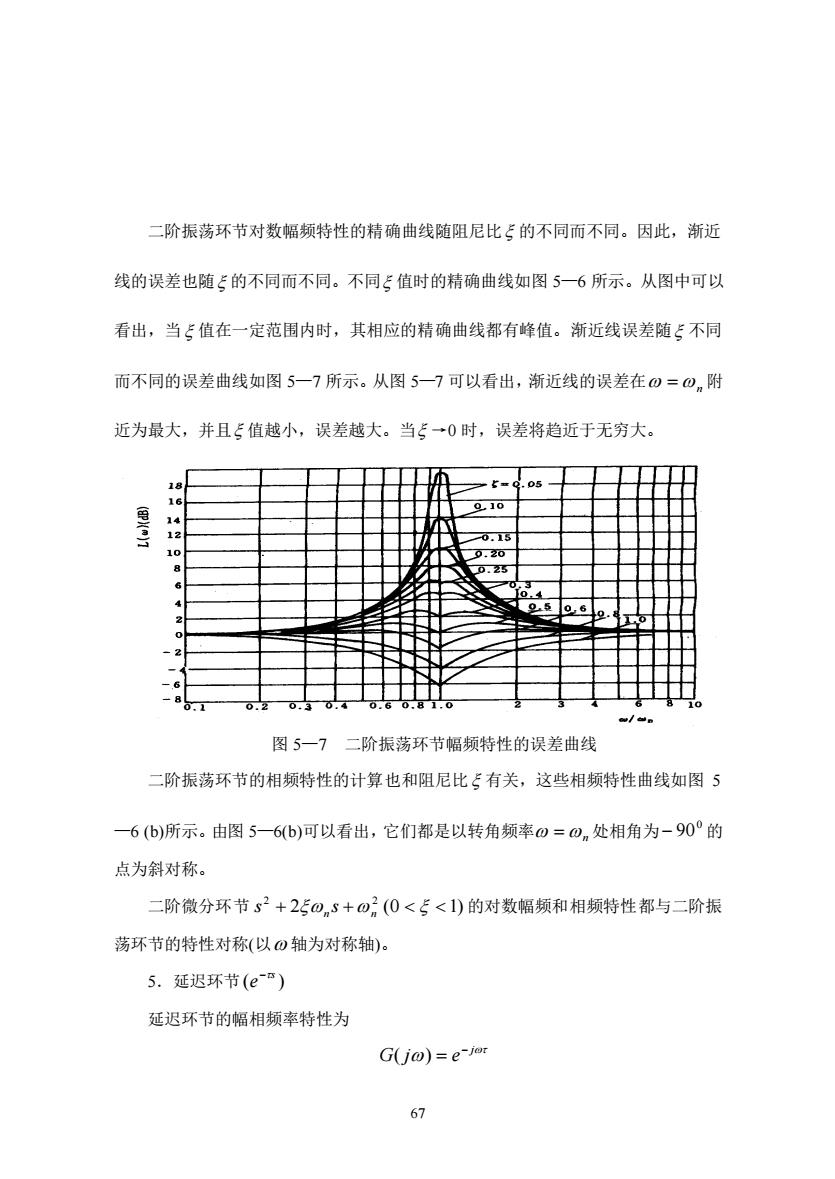
二阶振荡环节对数幅频特性的精确曲线随阻尼比5的不同而不同。因此，渐近 线的误差也随￡的不同而不同。不同￡值时的精确曲线如图5一6所示。从图中可以 看出，当5值在一定范围内时，其相应的精确曲线都有峰值。渐近线误差随5不同 而不同的误差曲线如图5一7所示。从图5一7可以看出，渐近线的误差在@=⊙.附 近为最大，并且5值越小，误差越大。当5→0时，误差将趋近于无穷大。 210 w/w 图5一7二阶振荡环节幅频特性的误差曲线 二阶振荡环节的相频特性的计算也和阻尼比ξ有关，这些相频特性曲线如图5 -6(b)所示。由图5一6(b)可以看出，它们都是以转角频率0=0n处相角为-90°的 点为斜对称。 二阶微分环节s2+250+o2(0<5<1)的对数幅频和相频特性都与二阶振 荡环节的特性对称（以0轴为对称轴） 5.延迟环节(ea) 延迟环节的幅相频率特性为 G(j@)=e-J: 6

67 二阶振荡环节对数幅频特性的精确曲线随阻尼比  的不同而不同。因此，渐近 线的误差也随  的不同而不同。不同  值时的精确曲线如图 5—6 所示。从图中可以 看出，当  值在一定范围内时，其相应的精确曲线都有峰值。渐近线误差随  不同 而不同的误差曲线如图 5—7 所示。从图 5—7 可以看出，渐近线的误差在  =n 附 近为最大，并且  值越小，误差越大。当  →0 时，误差将趋近于无穷大。 图 5—7 二阶振荡环节幅频特性的误差曲线 二阶振荡环节的相频特性的计算也和阻尼比  有关，这些相频特性曲线如图 5 —6 (b)所示。由图 5—6(b)可以看出，它们都是以转角频率  =n 处相角为 0 − 90 的 点为斜对称。 二阶微分环节 2 2 2 n n s +  s + (0    1) 的对数幅频和相频特性都与二阶振 荡环节的特性对称(以  轴为对称轴)。 5．延迟环节 ( ) s e − 延迟环节的幅相频率特性为   j G j e − ( ) =

其幅频和相频特性为 M(o)=1 p(o)=-t0 所以对数幅相频率特性为 L(o)=20g1=0 p(o)=-to(rad)=-57.3×to() 其对应的伯德图如图5一8所示。从图5一8可以看出，延迟环节的对数幅频特性 曲线为L(o)=0的直线，与0轴重合。相频特性曲线p(o)当0→∞时， p(0)-→-0。 图5-8延迟环节e-s的伯德图 5.2.2系统开环伯德图的绘制 【例5一1刂设系统的开环传递函数为 G(s)H(s)= 4(0.5s+1) s(2s+1)0.125s)2+0.05s+1 试绘制开环对数频率特性图（伯德图）。 解从系统的开环传递函数G(s)H(s)可知，系统由比例环节(4)、积分环节 、比例微分环节(0.5s+1)和二阶振荡环节 (2s+1月 1 1(0.1259)2+0.05s+1 等5个典型环节所组成，除比例环节和积分环节无转角频 68

68 其幅频和相频特性为    = − =     ( ) M ( ) 1 所以对数幅相频率特性为    = − = −  = = ( ) ( ) 57.3 ( ) ( ) 20lg1 0 0      rad L 其对应的伯德图如图 5—8 所示。从图 5—8 可以看出,延迟环节的对数幅频特性 曲线为 L() ＝0 的直线，与  轴重合。相频特性曲线 () 当  →∞时， () → −。 图 5-8 延迟环节 s e − 的伯德图 5.2.2 系统开环伯德图的绘制 [例 5—1] 设系统的开环传递函数为 (2 1)(0.125 ) 0.05 1 4(0.5 1) ( ) ( ) 2 + + + + = s s s s s G s H s 试绘制开环对数频率特性图(伯德图)。 解 从系统的开环传递函数 G(s)H(s) 可知，系统由比例环节(4)、积分环节       s 1 、惯性环节       2 +1 1 s 、比例微分环节 (0.5s +1) 和二阶振荡环节       (0.125 ) + 0.05 +1 1 2 s s 等 5 个典型环节所组成，除比例环节和积分环节无转角频

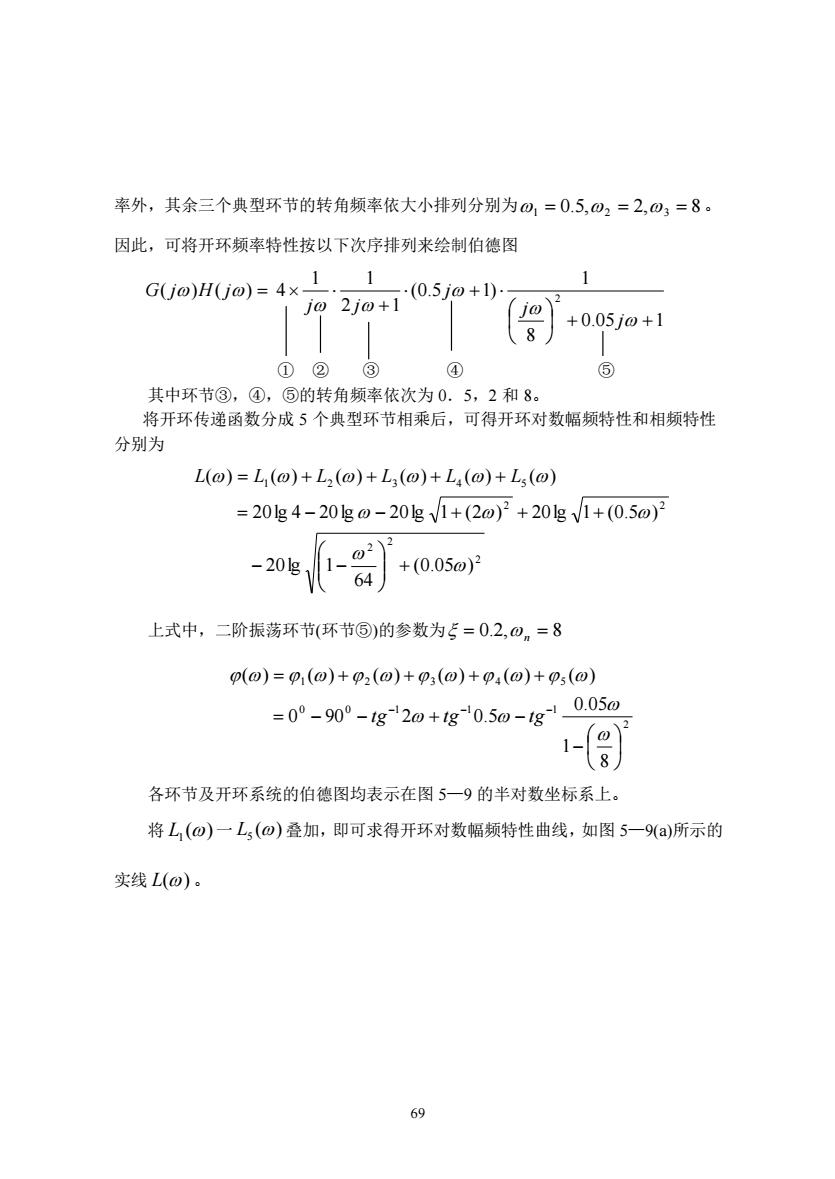
率外，其余三个典型环节的转角频率依大小排列分别为0，=0.5,02=2,0，=8。 因此，可将开环频率特性按以下次序排列来绘制伯德图 G(jo)H(jo)=4x1.1 1 (0.5j0+1)- j02j0+1 jo 8 +0.05j0+1 ①②③ ④④ ⑤ 其中环节③，④，⑤的转角频率依次为0.5,2和8。 将开环传递函数分成5个典型环节相乘后，可得开环对数幅频特性和相频特性 分别为 L(o)=L,(o)+L2(o)+L(o)+L,(o)+L(o) =20g4-20go-20gV1+(20)2+20gV1+(0.5o) +(0.05)月 上式中，二阶振荡环节（环节⑤）的参数为5=0.2,0n=8 p(o)=p(@)+p2(⊙)+p3(o)+p,(o)+p5(0) =0-90°-g20+g050-g000 各环节及开环系统的伯德图均表示在图5一9的半对数坐标系上。 将L,(o)一L,(o)叠加，即可求得开环对数幅频特性曲线，如图5一9(a)所示的 实线L(o)。 69

69 率外，其余三个典型环节的转角频率依大小排列分别为 1 = 0.5,2 = 2,3 = 8。 因此，可将开环频率特性按以下次序排列来绘制伯德图 0.05 1 8 1 (0.5 1) 2 1 1 1 ( ) ( ) 4 2  + +       +  + =          j j j j j G j H j ① ② ③ ④ ⑤ 其中环节③，④，⑤的转角频率依次为 0．5，2 和 8。 将开环传递函数分成 5 个典型环节相乘后，可得开环对数幅频特性和相频特性 分别为 2 2 2 2 2 1 2 3 4 5 (0.05 ) 64 20lg 1 20lg 4 20lg 20lg 1 (2 ) 20lg 1 (0.5 ) ( ) ( ) ( ) ( ) ( ) ( )            +         − − = − − + + + = + + + + L L L L L L 上式中，二阶振荡环节(环节⑤)的参数为  = 0.2,n = 8 2 0 0 1 1 1 1 2 3 4 5 8 1 0.05 0 90 2 0.5 ( ) ( ) ( ) ( ) ( ) ( )       − = − − + − = + + + + − − −                 tg tg tg 各环节及开环系统的伯德图均表示在图 5—9 的半对数坐标系上。 将 ( ) L1  一 ( ) L5  叠加，即可求得开环对数幅频特性曲线，如图 5—9(a)所示的 实线 L()