对控制系统来说,相位纯滞后越大,对系统的稳定性越不利,因此要尽量减小 延迟环节的影响和尽可能避免有非最小相位特性的元件。 5.3极坐标图 5.3.1典型环节频率特性的极坐标图 1,比例环节 比例环节的传递函数为 G(s)=K 所以比例环节的频率特性为 G(a)=K十j0=Ke0 其频率特性极坐标图如图5-11所示。其中幅值M(ω)=K。相位移中(o)=0°。 并且与无关它表示输出入的信且相仓相。 K R(o) 图5一11比例环节频率特性极坐标图 2.积分环节 积分环节的传递函数为 G(s)=1 所以积分环节的频率特性为 G(jo)= jo 其频率特性极坐标图如图5一12所示,它是整个负虚轴,且当∞时,趋向 原点0,显然积分环节是一个相位滞后环节[因为中(“)=-90],每当信号通过一个 积分环节,相位将滞后90
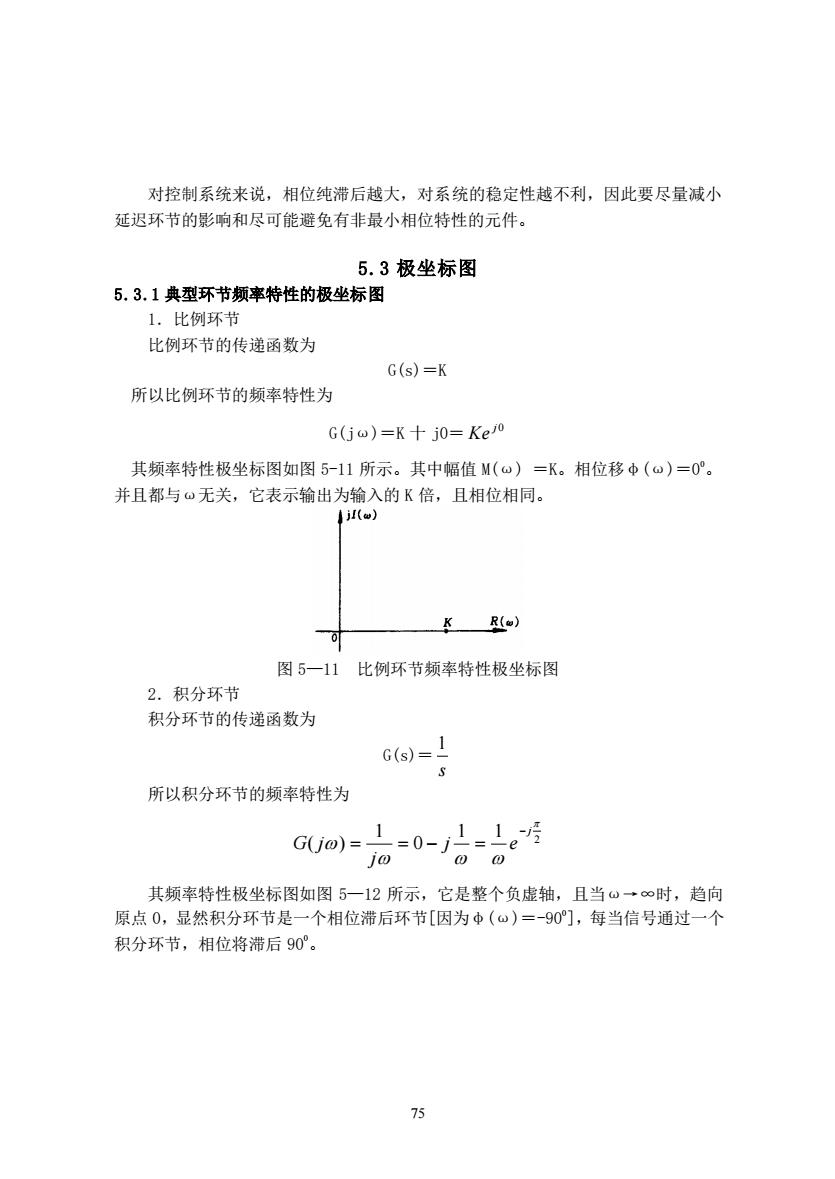
75 对控制系统来说,相位纯滞后越大,对系统的稳定性越不利,因此要尽量减小 延迟环节的影响和尽可能避免有非最小相位特性的元件。 5.3 极坐标图 5.3.1 典型环节频率特性的极坐标图 1.比例环节 比例环节的传递函数为 G(s)=K 所以比例环节的频率特性为 G(jω)=K 十 j0= j0 Ke 其频率特性极坐标图如图 5-11 所示。其中幅值 M(ω) =K。相位移φ(ω)=0 0。 并且都与ω无关,它表示输出为输入的 K 倍,且相位相同。 图 5—11 比例环节频率特性极坐标图 2.积分环节 积分环节的传递函数为 G(s)= s 1 所以积分环节的频率特性为 2 1 1 0 1 ( ) j j e j G j − = = − = 其频率特性极坐标图如图 5—12 所示,它是整个负虚轴,且当ω→∞时,趋向 原点 0,显然积分环节是一个相位滞后环节[因为φ(ω)=-90 0 ],每当信号通过一个 积分环节,相位将滞后 90 0
0 图5一12积分环节频率特性极坐标图 3.微分环节 微分环节的传递函数为 G(s)=s 所以微分环节的频率特性为 GU)=jo=0+jm=0e片 其极坐标图如图5一13所示。是整个正虚轴,恰好与积分环节的特性相反。其 幅值变化与w成正比:M(a)=a,当a=0时,M(o)也为零,当w→oo时,M(o) 也一∞。微分环节是一个相位超前环节[中()=+90]。系统中每增加一个微分环 节将使相位超前90°。 图5-13微分环节频率特性极坐标图 4.一阶惯性环节 阶惯性环节的传递函数为 G()=Ts+1 1 所以一阶惯性环节的频率特性为 1 1 To G(je)-I+jfo+To1+To 幅频特性和相频特性为
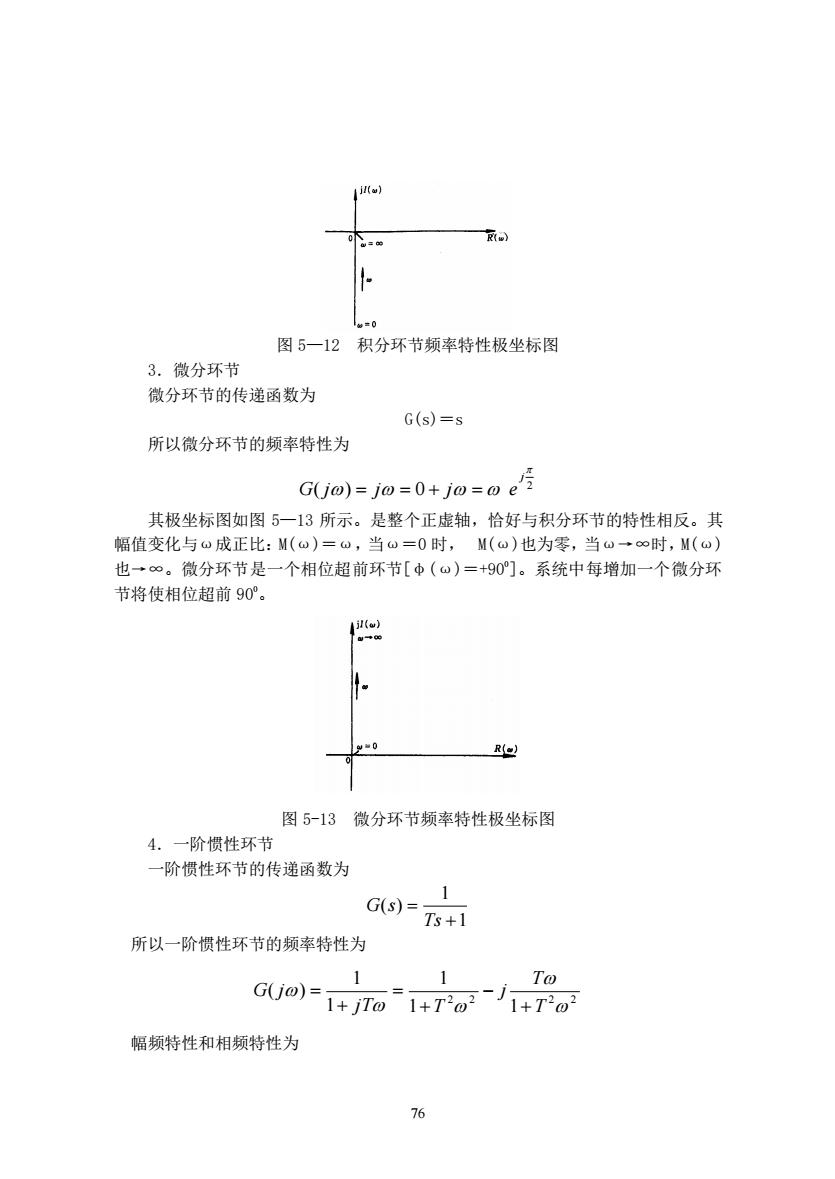
76 图 5—12 积分环节频率特性极坐标图 3.微分环节 微分环节的传递函数为 G(s)=s 所以微分环节的频率特性为 2 ( ) 0 j G j = j = + j = e 其极坐标图如图 5—13 所示。是整个正虚轴,恰好与积分环节的特性相反。其 幅值变化与ω成正比:M(ω)=ω,当ω=0 时, M(ω)也为零,当ω→∞时,M(ω) 也→∞。微分环节是一个相位超前环节[φ(ω)=+90 0 ]。系统中每增加一个微分环 节将使相位超前 90 0。 图 5-13 微分环节频率特性极坐标图 4.一阶惯性环节 一阶惯性环节的传递函数为 1 1 ( ) + = Ts G s 所以一阶惯性环节的频率特性为 2 2 2 2 1 1 1 1 1 ( ) T T j jT T G j + − + = + = 幅频特性和相频特性为