
部分习题分析与解答 第十四章机械振动 第十朦部分腾肯濞餐
部分习题分析与解答 第十四章机械振动
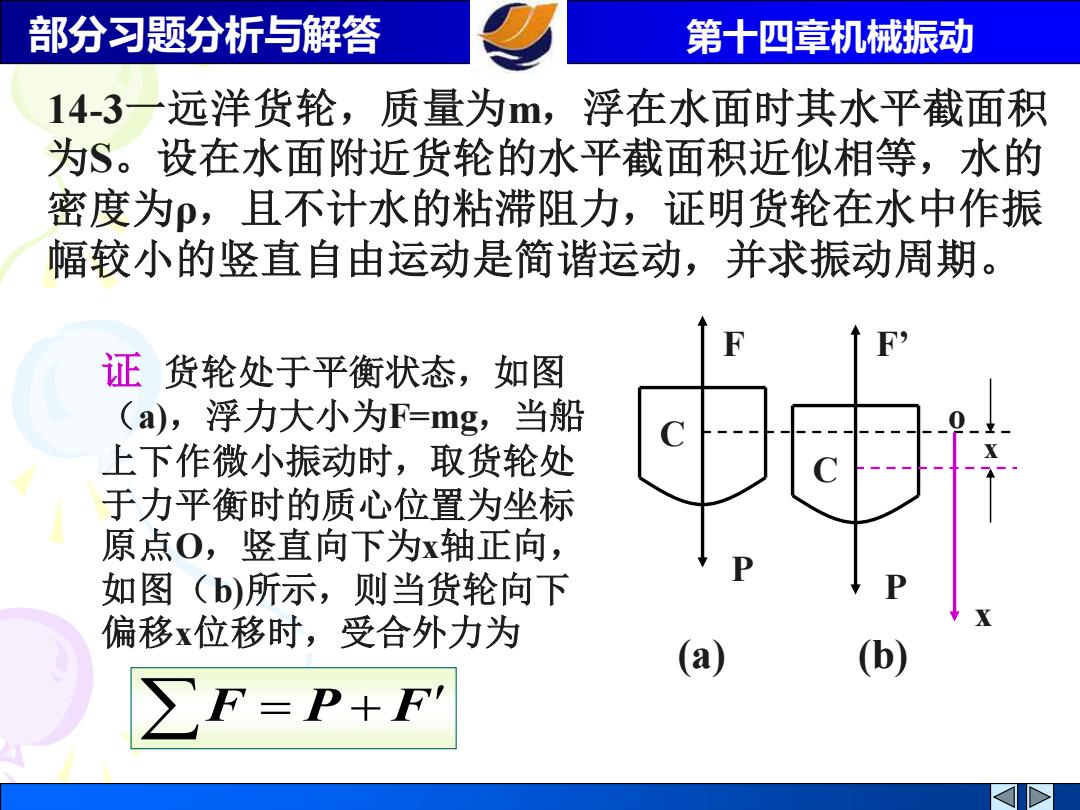
部分习题分析与解答 第十四章机械振动 14-3一远洋货轮,质量为m,浮在水面时其水平截面积 为S。设在水面附近货轮的水平截面积近似相等,水的 密度为,且不计水的粘滞阻力,证明货轮在水中作振 幅较小的竖直自由运动是简谐运动,并求振动周期。 证货轮处于平衡状态,如图 (a),浮力大小为F=mg,当船 上下作微小振动时,取货轮处 于力平衡时的质心位置为坐标 原点O,竖直向下为x轴正向, 如图(b)所示,则当货轮向下 偏移x位移时,受合外力为 (a) (b) ∑F=P+F
部分习题分析与解答 第十四章机械振动 证 货轮处于平衡状态,如图 (a),浮力大小为F=mg,当船 上下作微小振动时,取货轮处 于力平衡时的质心位置为坐标 原点O,竖直向下为x轴正向, 如图(b)所示,则当货轮向下 偏移x位移时,受合外力为 F = P +F 14-3一远洋货轮,质量为m,浮在水面时其水平截面积 为S。设在水面附近货轮的水平截面积近似相等,水的 密度为ρ,且不计水的粘滞阻力,证明货轮在水中作振 幅较小的竖直自由运动是简谐运动,并求振动周期。 F P C (a) P C F’ x o x (b)
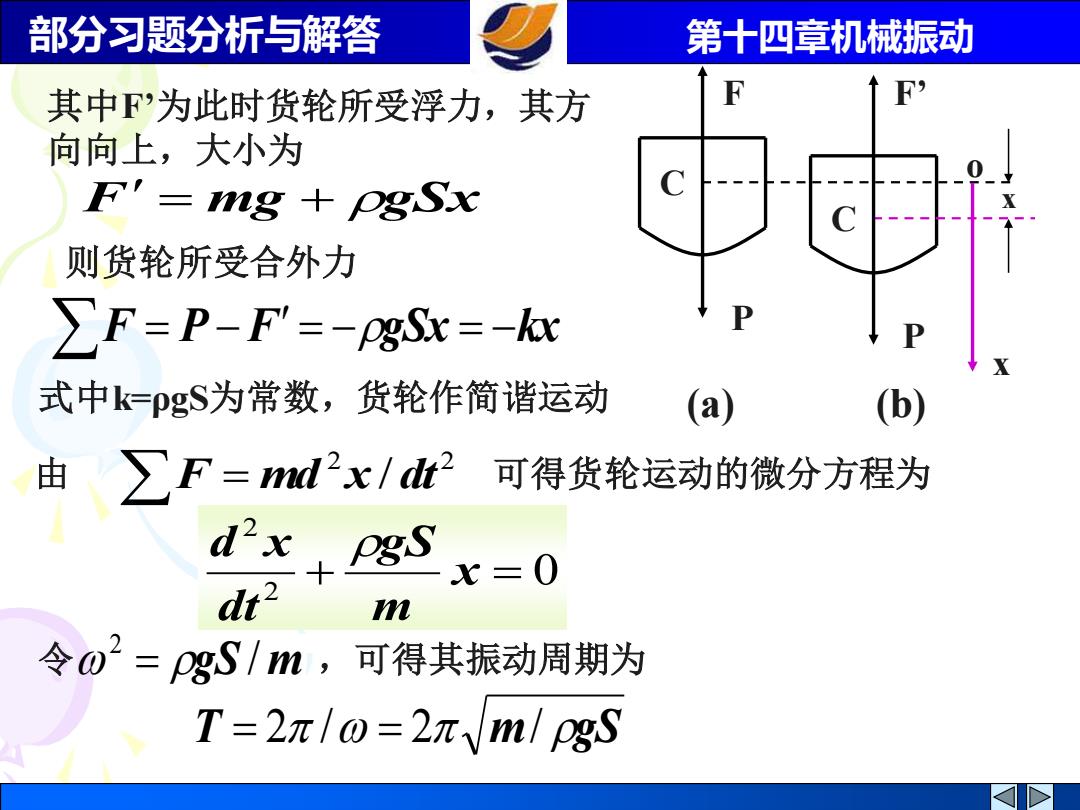
部分习题分析与解答 第十四章机械振动 其中℉为此时货轮所受浮力,其方 向向上,大小为 F'=ig +pgSx 则货轮所受合外力 ∑F=P-F'=-PgS=-lx 式中k=pgS为常数,货轮作简谐运动 (a) (b) 由 ∑F=l2x/dh2可得货轮运动的微分方程为 d2x x=0 dr2 m 令o2=pgS1m, 可得其振动周期为 T=2π/o=2πVm/pgS
部分习题分析与解答 第十四章机械振动 F = mg + gSx 其中F’为此时货轮所受浮力,其方 向向上,大小为 则货轮所受合外力 F = P −F = −gSx = −kx 式中k=ρgS为常数,货轮作简谐运动 0 2 2 + x = m gS dt d x 由 F = md 2 x / dt 2 可得货轮运动的微分方程为 令 gS / m ,可得其振动周期为 2 = T = 2 / = 2 m/ gS F P C (a) P C F’ x o x (b)

部分习题分析与解答 第十四章机械振动 14-5如图(a)所示,两个轻弹簧的劲度系数分别为k1和 k2,物体在光滑斜面上振动。(1)证明其运动仍是简 谐运动;(2)求系统的振动频率。 K 证设物体平衡时两弹簧伸长分别为x1、 x2,则物体受力平衡,有 mg sin 0=kx=k2x2 1) (a) 按图(b)所取坐标,物体沿x轴移动 位移x时,两弹簧又分别被拉伸x',和 x2,即x=x'1+x'2,则物体受力为 F=mg sin -k2 (x2+x2) (b) =mg sin e-k (x+x) (2)
部分习题分析与解答 第十四章机械振动 sin ( ) (2) sin ( ) 1 1 1 2 2 2 mg k x x F mg k x x = − + = − + 证 设物体平衡时两弹簧伸长分别为x1、 x2,则物体受力平衡,有 sin (1) mg = k1 x1 = k2 x2 按图(b)所取坐标,物体沿x轴移动 位移x时,两弹簧又分别被拉伸x’ 1 和 x’ 2,即x= x’ 1 +x’ 2,则物体受力为 14-5如图(a)所示,两个轻弹簧的劲度系数分别为k1和 k2,物体在光滑斜面上振动。(1)证明其运动仍是简 谐运动;(2)求系统的振动频率

部分习题分析与解答 第十四章机械振动 将式(1)代入式(2)得 F=-kx=-k2x2 (3) 由式(3)得x=-F/k,,=-F/k2) 而x=X1+x2,则得到 kk2 (b) F-- x=-kox k +k2 式中k=kk,(k,+k,)为常数,则物体作简谐运 动,振动频率为 01 kk2 /(k+k2)m 2π1 2πVm 2元 讨论:斜面倾角对弹簧作简谐运动及振动的频率均不产生影响
部分习题分析与解答 第十四章机械振动 x kx k k k k F = − + = − 1 2 1 2 将式(1)代入式(2)得 (3) F k1 x1 k2 x2 = − = − 由式(3)得 而x= x’ 1 +x’ 2, ,则得到 / , / ) 1 1 2 2 x = −F k x = −F k 式中 为常数,则物体作简谐运 动,振动频率为 /( ) k = k1 k2 k1 + k2 k k k k m m k /( ) 2 1 2 1 2 = = = 1 2 1 + 2 讨论:斜面倾角对弹簧作简谐运动及振动的频率均不产生影响