广东海洋大学：《大学物理》课程教学资源（习题分析与解答）第八章 静电场

第八章 静电场部分习题分析与解答 第小章部分同题仟与掷餐

第八章 静电场部分习题分析与解答

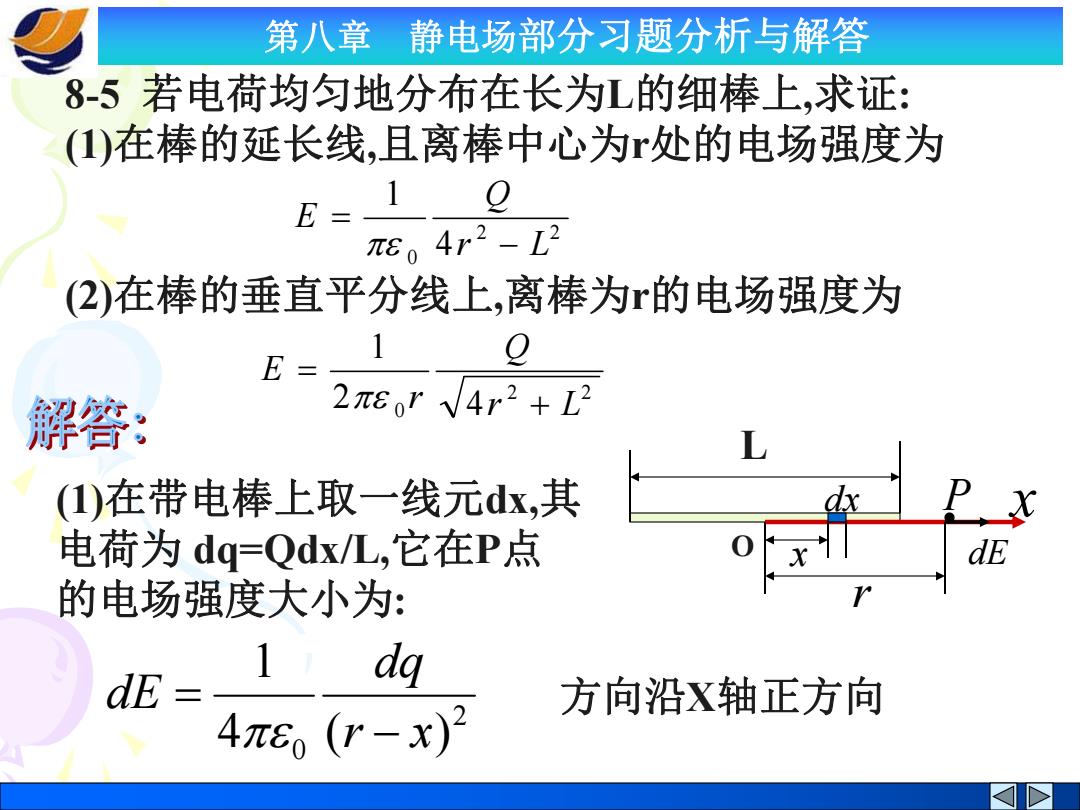
第八章 静电场部分习题分析与解答 8-5若电荷均匀地分布在长为L的细棒上，求证： ()在棒的延长线，且离棒中心为r处的电场强度为 E=_ Q 6.4r2-L2 (2)在棒的垂直平分线上，离棒为的电场强度为 E= Q 解答： 2πE0rV4r2+L2 (1)在带电棒上取一线元dx,其 电荷为dq=Qdx/L,它在P点 dE 的电场强度大小为： 1 dE dq 方向沿X轴正方向 4π6(r-x)2

第八章 静电场部分习题分析与解答 8-5 若电荷均匀地分布在长为L的细棒上,求证: (1)在棒的延长线,且离棒中心为r处的电场强度为 (2)在棒的垂直平分线上,离棒为r的电场强度为 2 2 0 4 1 r L Q E    2 2 2 0 4 1 r L Q r E    (1)在带电棒上取一线元dx,其 电荷为 dq=Qdx/L,它在P点 的电场强度大小为: 2 0 4 ( ) 1 r x dq dE    方向沿X轴正方向 L O dx x x P r dE

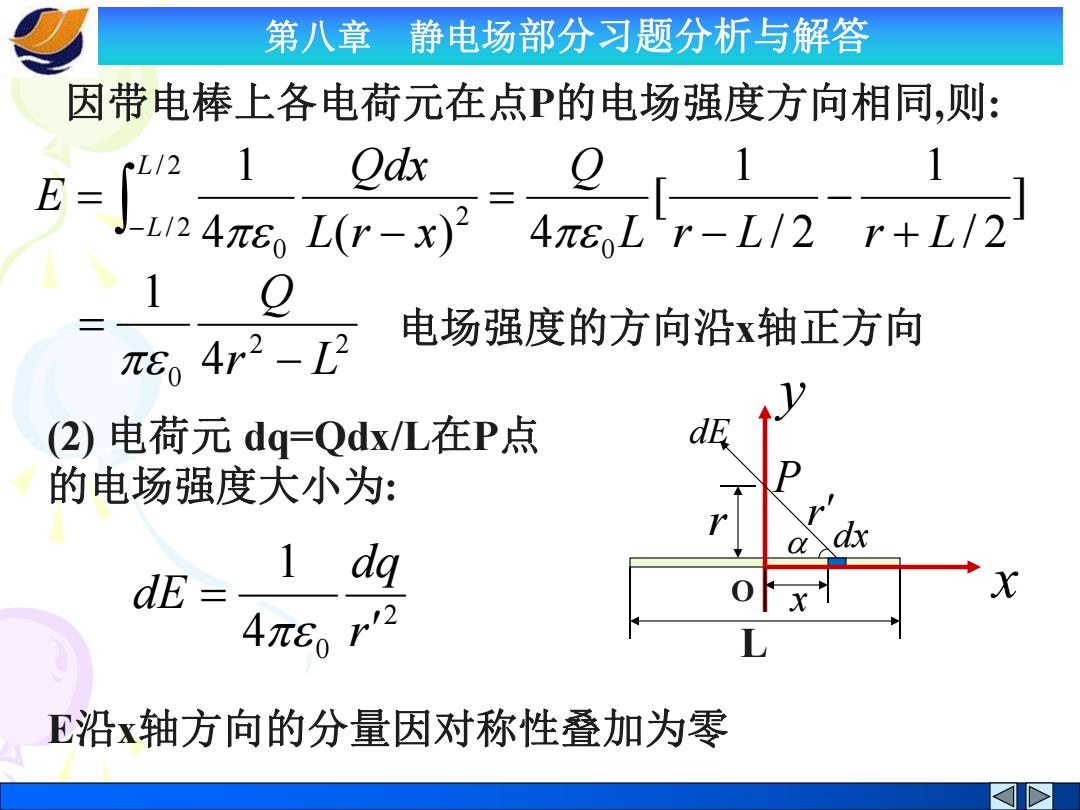
第八章 静电场部分习题分析与解答 因带电棒上各电荷元在点P的电场强度方向相同，则： L/2 1 E= Odx J-L24π6。L(r-x)24 Q E,4r2-L2 电场强度的方向沿x轴正方向 (2)电荷元dq=Qdx/L在P点 的电场强度大小为： dE dq 4πr2 E沿x轴方向的分量因对称性叠加为零

第八章 静电场部分习题分析与解答 因带电棒上各电荷元在点P的电场强度方向相同,则: ] / 2 1 / 2 1 [ 4 ( ) 4 1 0 / 2 / 2 2 0 L r L r L Q L r x Qdx E L L          2 2 0 4 1 r L Q    电场强度的方向沿x轴正方向 (2) 电荷元 dq=Qdx/L在P点 的电场强度大小为: L O x dx x P r r  dE y  2 0 4 1 r dq dE    E沿x轴方向的分量因对称性叠加为零

第八章 静电场部分习题分析与解答 故，点P的电场强度大小为 -,-[逃，1wiE- sin adq F方向沿y轴的正方向 因为sina=r/r',r'=Vr2+x2统一积分变量，则 L/2 rOdx Q E=24（+r 2π8rVL2+4r2 当棒长L→0时，P点的电场强度为 1 E=lim- Q/L λ L→∞2π8orV1+4r2/L2 2π8or 此结果与无限长带电直线周围的电场强度分布相同

第八章 静电场部分习题分析与解答 故,点P的电场强度大小为:         L L L y y r dq E E dE dE 2 4 0 sin sin    因为 sin  r /r  , r   r 2  x 2 统一积分变量,则 E方向沿y轴的正方向  2 2 / 2 / 2 0 2 2 3/ 2 0 2 4 1 4 ( ) L r Q x r r rQdx E L L        当棒长 L   时,P点的电场强度为 L r r Q L r E L 0 2 2 0 1 4 / 2 / 2 1 lim        此结果与无限长带电直线周围的电场强度分布相同

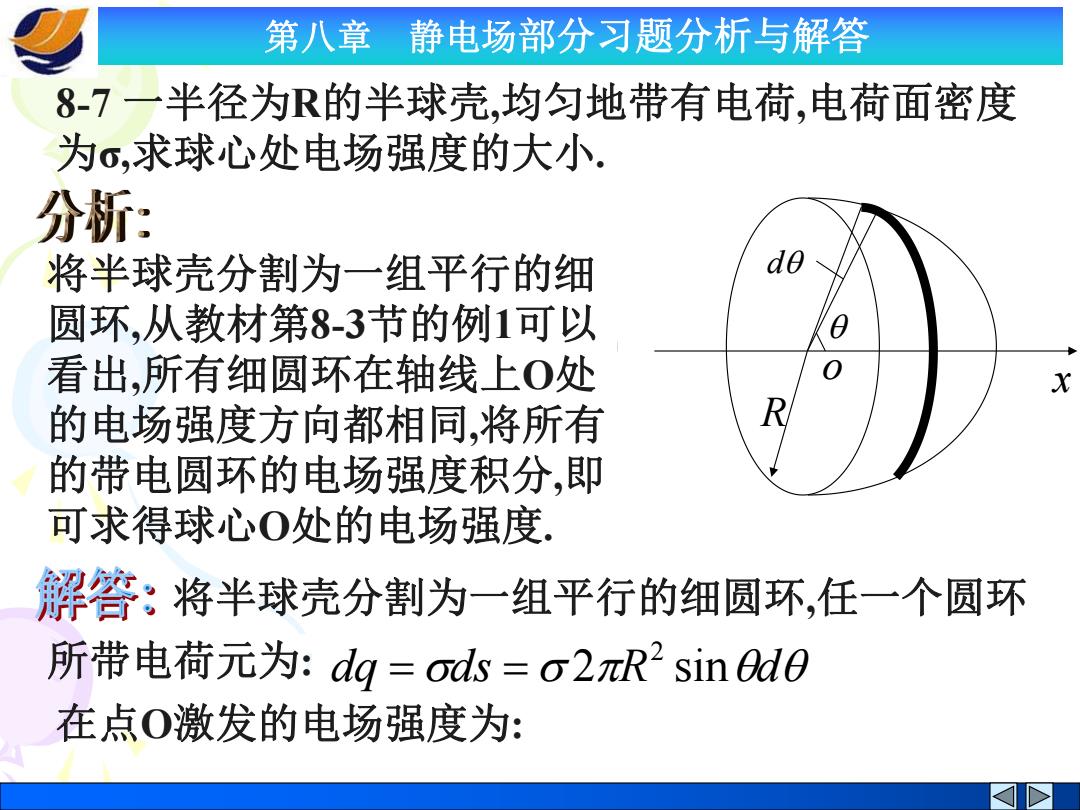
第八章静电场部分习题分析与解答 8-7一半径为R的半球壳，均匀地带有电荷，电荷面密度 为ō，求球心处电场强度的大小. 分析： 将半球壳分割为一组平行的细 do 圆环，从教材第83节的例1可以 看出，所有细圆环在轴线上0处 的电场强度方向都相同，将所有 R 的带电圆环的电场强度积分，即 可求得球心O处的电场强度！ 解答：将半球壳分割为一组平行的细圆环，任一个圆环 所带电荷元为：dg=ods=o2πR2sind0 在点O激发的电场强度为：

第八章 静电场部分习题分析与解答 8-7 一半径为R的半球壳,均匀地带有电荷,电荷面密度 为σ,求球心处电场强度的大小. 将半球壳分割为一组平行的细 圆环,从教材第8-3节的例1可以 看出,所有细圆环在轴线上O处 的电场强度方向都相同,将所有 的带电圆环的电场强度积分,即 可求得球心O处的电场强度. R o  d x dq ds  2R sind 2 所带电荷元为:   将半球壳分割为一组平行的细圆环,任一个圆环 在点O激发的电场强度为: