
第十一章 稳恒磁场部分习题分析与解答 第卜章粉氨箭离餐
第十一章 稳恒磁场部分习题分析与解答

第十一章稳恒磁场部分习题分析与解答 11-4 如图所示,几种载流导线在平面内分布,电 流均为,它们在点O的磁感强度各为多少? 解:(a)长直电流对点O而言,有Idxr=O,因此它在点 O产生的磁场为零,则点0处总的磁感强度为1/4圆弧 电流所激发,故有 8R 方向垂直纸面向外
第十一章 稳恒磁场部分习题分析与解答 11-4 如图所示,几种载流导线在平面内分布,电 流均为I,它们在点O的磁感强度各为多少? 解: (a)长直电流对点O而言,有Idℓ r=0,因此它在点 O产生的磁场为零,则点O处总的磁感强度为1/4圆弧 电流所激发,故有 R I B 8 0 0 方向垂直纸面向外
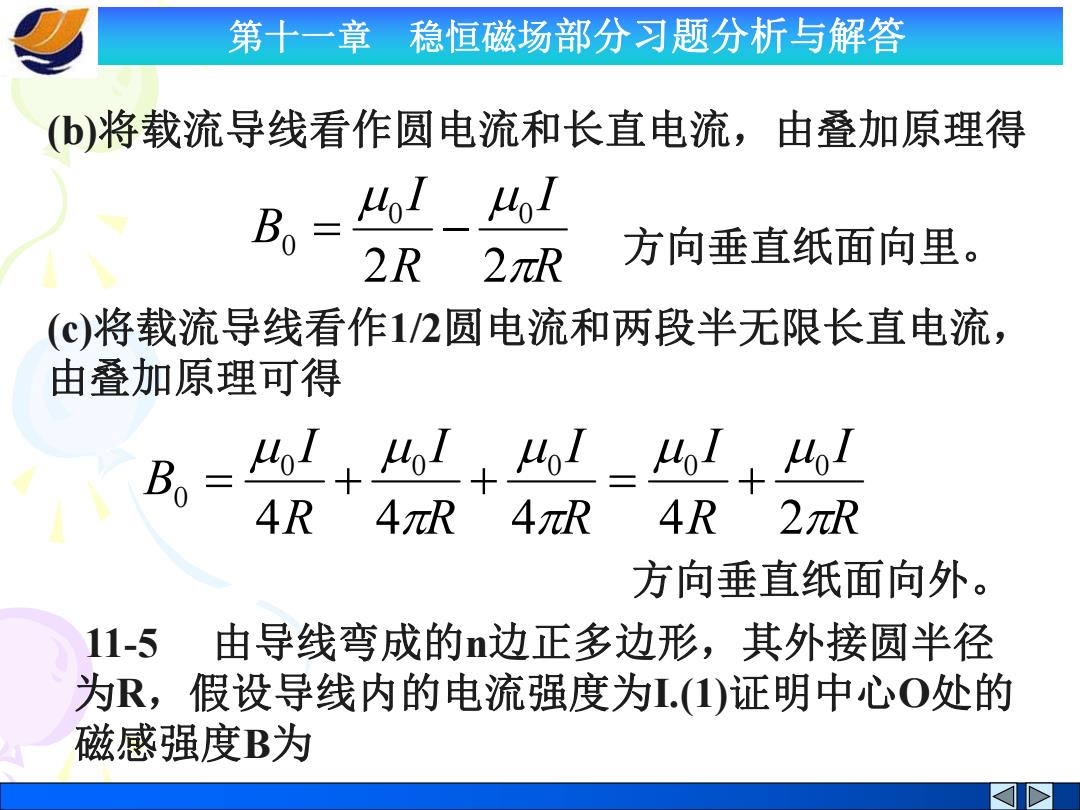
第十一章 稳恒磁场部分习题分析与解答 ()将载流导线看作圆电流和长直电流,由叠加原理得 B。= 4,I4I 2R 2πR 方向垂直纸面向里。 (c)将载流导线看作1/2圆电流和两段半无限长直电流, 由叠加原理可得 +41 4I4114I 4R 4πR 4πR 4R 2R 方向垂直纸面向外。 11-5 由导线弯成的n边正多边形,其外接圆半径 为R,假设导线内的电流强度为L.(1)证明中心O处的 磁感强度B为
第十一章 稳恒磁场部分习题分析与解答 (b)将载流导线看作圆电流和长直电流,由叠加原理得 R I R I B 2 2 0 0 0 方向垂直纸面向里。 (c)将载流导线看作1/2圆电流和两段半无限长直电流, 由叠加原理可得 R I R I R I R I R I B 4 4 4 4 2 0 0 0 0 0 0 方向垂直纸面向外。 11-5 由导线弯成的n边正多边形,其外接圆半径 为R,假设导线内的电流强度为I.(1)证明中心O处的 磁感强度B为

第十一章 稳恒磁场部分习题分析与解答 B=Honl tg( 2πR (2)证明当n→∞时,B等于载流圆环中心的磁感强度. 证:(1)将载流导线 分解成如图所示的n段 等长的载流直导线,根 据磁场的叠加原理,可 求得点O的磁感强度B。 第段载流直导线 在O点的磁感强度为: B. 4
第十一章 稳恒磁场部分习题分析与解答 ( ) 2 0 n tg R nI B (2)证明当n →∞时,B等于载流圆环中心的磁感强度. 证: (1)将载流导线 分解成如图所示的n段 等长的载流直导线,根 据磁场的叠加原理,可 求得点O的磁感强度B。 第i段载流直导线 在O点的磁感强度为: )] 2 2 ) cos( 2 2 [cos( 4 0 r I Bi

第十一章 稳恒磁场部分习题分析与解答 2 B的方向垂直纸面向外,段等长的载流直导线在点 O激发的磁场方向相同,因而点O的磁感强度大小为: B=nB 由几何关系r=Rcos(△p/2)和△0=2π/n,代入并整理,得 B=nB =) 2πR n (2)当n→oo时,正n边形趋于半径为R的外接圆,由上 式可得点O的磁感强度B的值为 sin() B=lm∑B=lim以g5)=lim 71 n n->oo n→02πR n→2R cos(") 2R
第十一章 稳恒磁场部分习题分析与解答 ) 2 sin( 2 0 r I Bi Bi的方向垂直纸面向外,n段等长的载流直导线在点 O激发的磁场方向相同,因而点O的磁感强度大小为: i B nB 由几何关系r=Rcos(Δφ/2)和Δφ=2π/n,代入并整理,得 ( ) 2 0 n tg R nI B nBi (2)当n →∞时,正n边形趋于半径为R的外接圆,由上 式可得点O的磁感强度B的值为 R I n n n R I n tg R nI B B n n i n 2 ( ) sin( ) cos( ) 1 2 ( ) lim 2 lim lim 0 0 0