
第二章牛顿定律部分习题分析与解答 第典章分可翼分桥解答
第二章 牛顿定律部分习题分析与解答

第二章牛顿定律部分习题分析与解答 2-2假使地球自转速度加快到能使赤道上的物体处于 失重状态,一昼夜的时间有多长? 分新:由于物体地球自转时,有向心加速度存在当 提供此加速度的力即为重力时,物体处于失重 状态,由向心加速度和角速度的关系就可得一 昼夜所需的时间. 解倍:按题意有:mg=m7w2-mr(2不) 则地球自转一天所需的时间为: T=2πVr/g=2πV6.378×10619.8 =5.07×103s≈1.4h
第二章 牛顿定律部分习题分析与解答 2-2 假使地球自转速度加快到能使赤道上的物体处于 失重状态,一昼夜的时间有多长? 按题意有: 2 2 ) 2 ( T m g m r m r = = 由于物体地球自转时,有向心加速度存在.当 提供此加速度的力即为重力时,物体处于失重 状态,由向心加速度和角速度的关系就可得一 昼夜所需的时间. 则地球自转一天所需的时间为: s h T r g 5.07 10 1.4 2 / 2 6.378 10 / 9.8 3 6 = = =
第二章牛顿定律部分习题分析与解答 2-4图示一斜面,倾角为o,底边AB长为=2.1m,质量为m 的物体从斜面顶端由静止开始向下滑动,斜面的摩擦 因数为=0.14.试问,当o为何值时,物体在斜面上下滑 的时间最短?其数值为多少? 分新:该题关键在列出动力学和运动学方程后,解出 倾角与时间的函数关系=(①),然后运用对求 极值的方法即可得出数值来。 0 解答: 取沿斜面为坐标轴Ox, 原点O位于斜面顶点, 则由牛顿第二定律有 mg sin a-mgu cosa ma
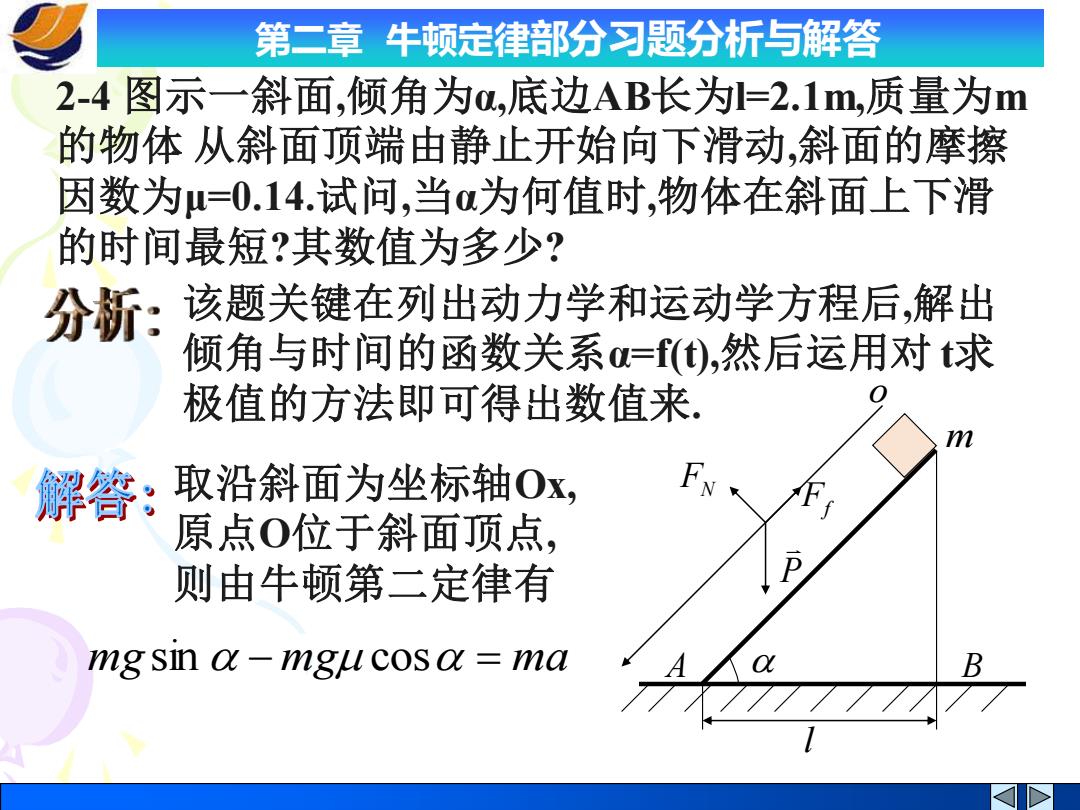
第二章 牛顿定律部分习题分析与解答 2-4 图示一斜面,倾角为α,底边AB长为l=2.1m,质量为m 的物体 从斜面顶端由静止开始向下滑动,斜面的摩擦 因数为μ=0.14.试问,当α为何值时,物体在斜面上下滑 的时间最短?其数值为多少? 取沿斜面为坐标轴Ox, 原点O位于斜面顶点, 则由牛顿第二定律有 mg sin − mg cos = ma 该题关键在列出动力学和运动学方程后,解出 倾角与时间的函数关系α=f(t),然后运用对 t求 极值的方法即可得出数值来. P Ff FN o m A B l

第二章牛顿定律部分习题分析与解答 又物体在斜面上作匀变速直线运动,故有: 1 1/cosa=-at =。8(sina-ucosa)t 2 21 则: t= g cosa(sin a-ucosa) 为使下滑时间最短,可令dt/da=O,由上式得: sin a(sin a-ucosa)+cosa(cosa+usin a)=0 则可得: tg20=-1/4, c=490 21 此时: =0.99s g cosa(sin a-ucosa)
第二章 牛顿定律部分习题分析与解答 又物体在斜面上作匀变速直线运动,故有: 2 2 (sin cos ) 2 1 2 1 l / cos = at = g − t 则: cos (sin cos ) 2 − = g l t 为使下滑时间最短,可令 dt / d = 0 ,由上式得: −sin (sin − cos) + cos(cos + sin ) = 0 则可得: 0 t g2 = −1/ , = 49 此时: s g l t 0.99 cos (sin cos ) 2 min = − =

第二章牛顿定律部分习题分析与解答 2-8直升飞机的螺旋桨由两个对称的叶片组成.每 一叶片的质量=136kg,长=3.66m,求当它的转速 n=320r/min时,两个叶片根部的张力.(设叶片是宽 度一定、厚度均匀的薄片) 分新:螺旋桨旋转时,叶片上各点的加速度不同,在 其各部分两侧的张力也不同;由于叶片的质量 是连续分布的,在求叶片根部的张力时,可选 取叶片上一小段,分析其受力,列出动力学方 程,然后采用积分的方法求解
第二章 牛顿定律部分习题分析与解答 2-8 直升飞机的螺旋桨由两个对称的叶片组成.每 一叶片的质量m=136kg,长l=3.66m,求当它的转速 n=320r/min时,两个叶片根部的张力.(设叶片是宽 度一定、厚度均匀的薄片) 螺旋桨旋转时,叶片上各点的加速度不同,在 其各部分两侧的张力也不同;由于叶片的质量 是连续分布的,在求叶片根部的张力时,可选 取叶片上一小段,分析其受力,列出动力学方 程,然后采用积分的方法求解