作业13—16 证明:连接OP、OQ,设想在PQO 的闭合导体回路中,由于OP、 OQ沿半径方向,于通过该处的感 应电场强度E处处垂直,故有: Sop=lopEdi=0; eo-oE●di=0 即OP、OP段均无电动势,由法拉第电磁感应定律求出 的闭合回路的总电动势,就是导体棒PQ上的电动势。 dB dB I 二BA0PO dΦ dt dt dt 21 2-
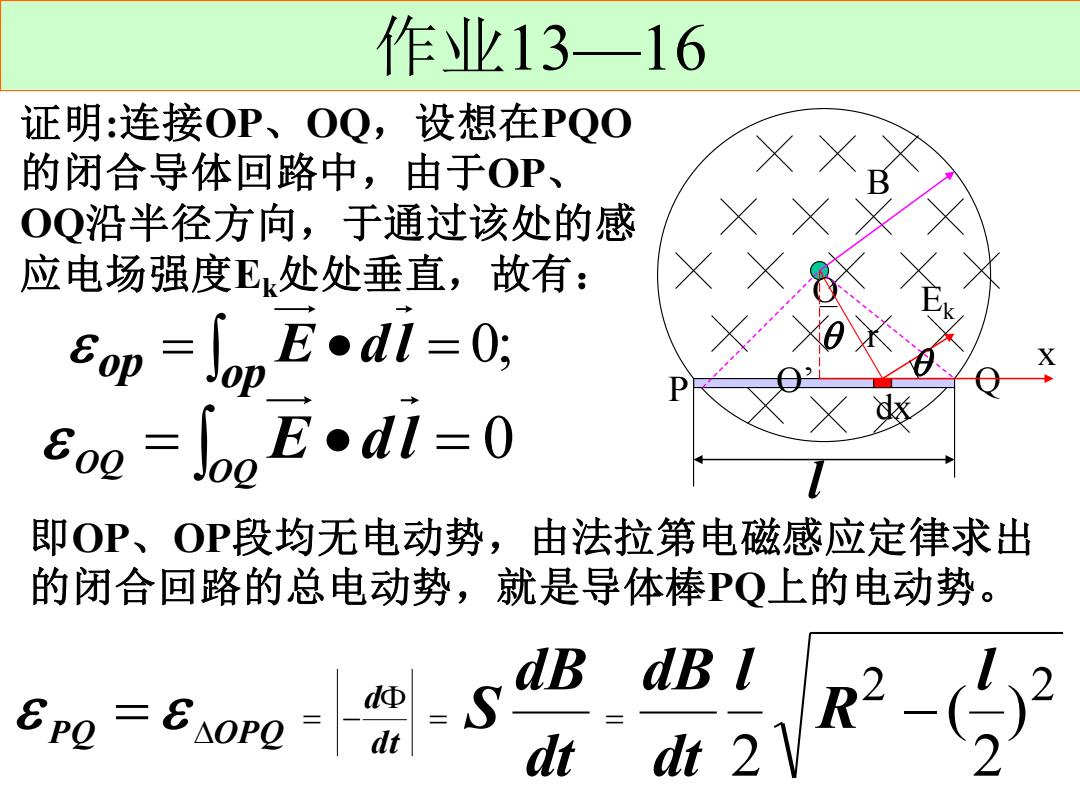
作业13—16 Q O P B l x dx O’ Ek r 证明:连接OP、OQ,设想在PQO 的闭合导体回路中,由于OP、 OQ沿半径方向,于通过该处的感 应电场强度Ek处处垂直,故有: = • = 0; E dl op op = E • dl = 0 OQ OQ 即OP、OP段均无电动势,由法拉第电磁感应定律求出 的闭合回路的总电动势,就是导体棒PQ上的电动势。 2 2 ) 2 ( 2 l R l dt dB dt dB S d t d P Q = OPQ = = − = −

作业13-21 解:两平行长直导线可以看成是无限 长但宽度为d的矩形回路的一部分。设 在回路中通有逆时针方向的电流I,然 后计算图中阴影部分的磁通量。该区 域内的磁场可以看成两无限长直导线 d 分别在该区域产生的磁场的叠加。 两平行导线间的磁感应强度为:B= 02 2π(d-r) 磁通量为:D=∫BS=Bd_ _d-a Φ 则长为的一对导线的自感为:L=
作业13 —21 r d I I l O 解:两平行长直导线可以看成是无限 长但宽度为 d的矩形回路的一部分。设 在回路中通有逆时针方向的电流 I,然 后计算图中阴影部分的磁通量。该区 域内的磁场可以看成两无限长直导线 分别在该区域产生的磁场的叠加。 2 2 ( ) 0 0d r I rI B − = + 两平行导线间的磁感应强度为: a Il d a B dS Bldr d a a S − = • = = − l n 0 磁通量为: a l d a I l L − = = l n 0 则长为 的一对导线的自感为:
作业13—22 解:(1)当A和A'连接时,AB 和AB线圈中的电流流向相反, 且由于两线圈紧密结合,通过 回路的磁通量也相反,故穿过 大回路的总通量为:①1=0,故L1=0 (2)当A和B连接时,AB和AB线圈中的电流流向相同, 且由于两线圈紧密结合,通过回路的磁通量也相同,故穿 过大回路的总通量为: Φ2=2Φ+2Φ=4Φ,故L2= =4 -=4L 可参阅赵凯华的《电磁学》下册第五章“两个线圈串连的 自感系数”内容
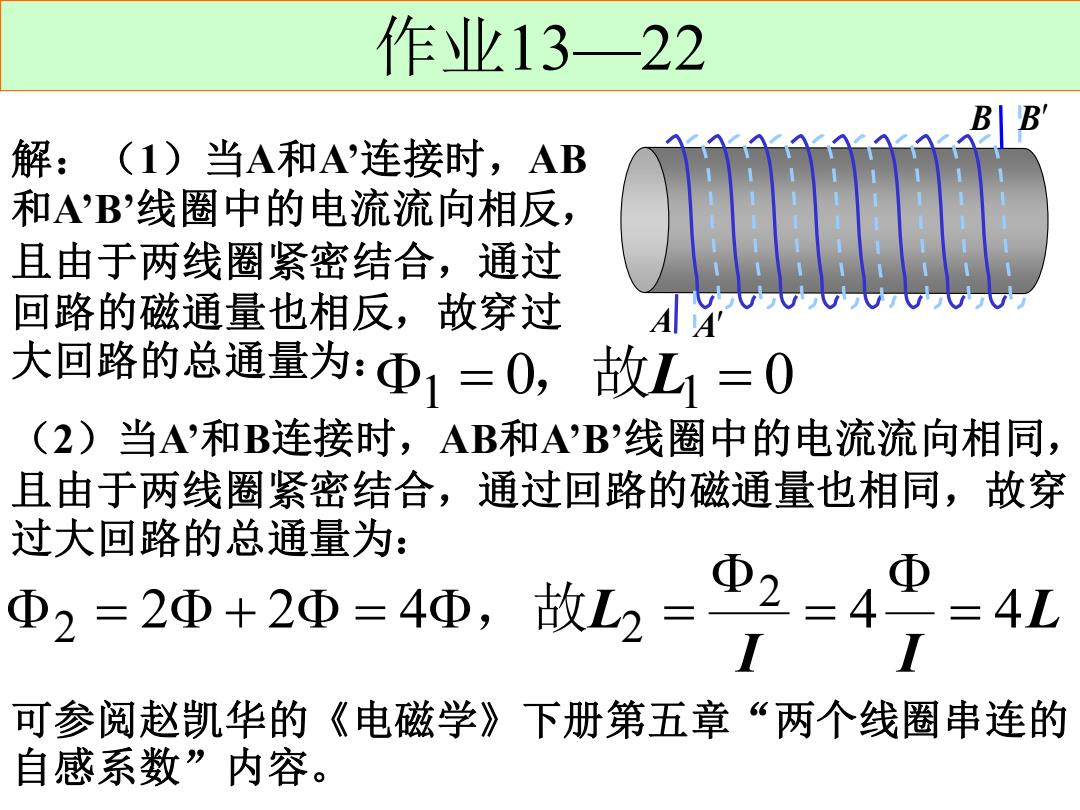
作业13—22 A B A B 解:(1)当A和A’连接时,AB 和A’B’线圈中的电流流向相反, 且由于两线圈紧密结合,通过 回路的磁通量也相反,故穿过 大回路的总通量为: 1 = 0,故L1 = 0 (2)当A’和B连接时,AB和A’B’线圈中的电流流向相同, 且由于两线圈紧密结合,通过回路的磁通量也相同,故穿 过大回路的总通量为: L I I 2 2 4 L 4 4 2 2 2 = = = + = ,故 = 可参阅赵凯华的《电磁学》下册第五章“两个线圈串连的 自感系数”内容
补充 B 3A B' B' 设线圈中产生的感应电动势为8, 设线圈对线圈产生的互感电动势为ε 线圈1中的电动势为:1+621=-(L1 d -M dt dt 线圈2中的电动势为:2+812=-(L d
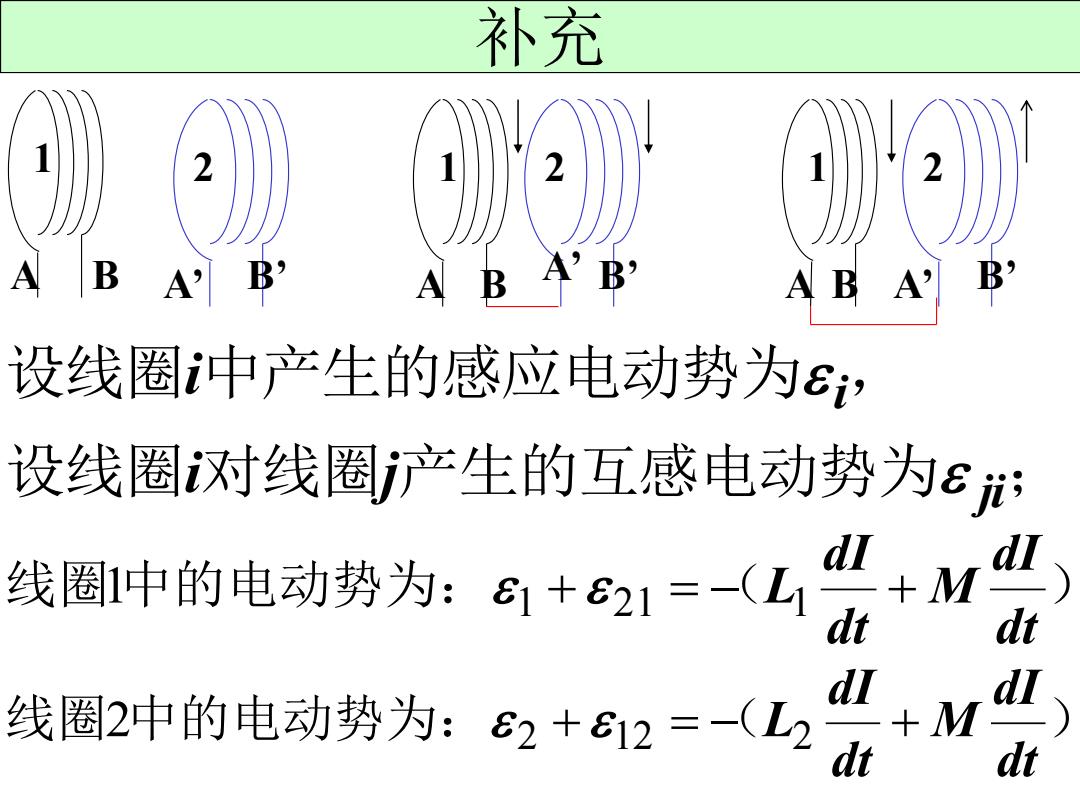
补充 1 A B 2 A’ B’ 1 A B 2 A’ B’ 1 A B 2 A’ B’ 设线圈i中产生的感应电动势为 i , 设线圈i对线圈j产生的互感电动势为 ji; 线圈 中的电动势为: ( ) dt dI M dt dI 1 1 + 21 = − L1 + 线圈 中的电动势为: ( ) dt dI M dt dI 2 2 + 12 = − L2 +

补充 如此图所示相联,两线圈中的电流流 向相同,则线圈中总的感应电动势为: A'B' £=81+B21+82+612 h-L=山+62M d d =-(L1+L2+2M) dt 如此图所示相联,两线圈中的电流流 向相反,则线圈中总的感应电动势为: AB A B 8=61-821+82-612 =4+h2w出1%1=h+-2M
补充 1 A B 2 A’ B’ 如此图所示相联,两线圈中的电流流 向相同,则线圈中总的感应电动势为: dt dI L dt dI = −(L1 + L2 + 2M) = − 1 21 2 12 = + + + L = L1 + L2 + 2M 1 A B 2 A’ B’ 如此图所示相联,两线圈中的电流流 向相反,则线圈中总的感应电动势为: 1 21 2 12 = − + − dt dI L dt dI = −(L1 + L2 − 2M) = − L = L1 + L2 − 2M