新疆大学：《自动控制理论》课程教学课件（PPT讲稿）第三章 控制系统的时域分析

自动控制理论 或写作 C0)=1 V1-5 V1-2 t20) 当5=0时，S12=±j⊙，则 C(t)=1-cos@t 2、临界阻尼（ξ=） 当5=0时，S12=-0n 02=1-0 c)43ae+5fs+a 1 C(t)=1-(1+@,t)e-@v 图3-9二阶系统的实极点 11 第三章控制系统的时域分析 2025/1/14

11 第三章 控制系统的时域分析 2025/1/14 当 = 0时,s1.2 =  jn则 自动控制理论 ( ) (t 0) 1 sin arctan 1 1 1 2 2          − + − = − −      C t e t d t n 或写作 C(t) t d =1− cos 2、 临界阻尼( =1) n 当 = 0时,s1.2 = − ( ) ( ) ( ) n n n n n s s s s C s        + − + = − + = 1 1 2 2 2 2 ( ) ( ) t n n C t t e   − = 1− 1+ 图3-9 二阶系统的实极点

自动控制理论 3、过阻尼(5>1) S12=-50,±0nV52-1 cs)= A A A 52+250s+oss+5,-0n52-1's+5@,+0nV52-1 2 A,=1 -1 42W-2-司 42+-司 C0)=1+4,e(-可w+A,e(+ve) 二附中阻尼系统的近似处理 Cg-=5o,-05-1 R(s)s+51 5+50,-0nV52-1 令r6)=,则 12 第三章控制系统的时域分析 2025/1/14

12 第三章 控制系统的时域分析 2025/1/14 ( ) t t n n C t A e A e             − + −      − − − = + + 1 3 1 2 2 2 1 自动控制理论 3、 过阻尼(＞1) s 1 2 1.2 = − n n  − ( ) ( 2 ) 1 1 2 3 2 1 2 2 2 2 + + − + + − − = − + + =             n d n n n n n s A s A s A s s s C s A1 =1 2 1( 1) 1 2 2 2 − − − − =    A 2 1( 1) 1 2 2 3 − + − =    A 二附中阻尼系统的近似处理 ( ) ( ) 1 1 2 2 1 1 + − − − − = + =         n n n n s s s s R s C s 令 ( ) ,则 s R s 1 =

自动控制理论 C(s)=- 50,-0nV52-11 +50n-0V52-1ss+50,-0nV52-1 C0=1-efs®可 如令on=1,5=p,则输出响应的准确值为 Cd=1+0.077e3.731-1.077e-0.o2n c(t) 近似计算值：C0)=1-eo27 允许偏差±4 三、二阶系统阶跃响应的性能指标 1、上升时间 当被控制量c()首次由零上升到其稳态值 所需的时间，称上升时间t, ct,)=1- 1 esin(oat,+β)=l 图3-13二阶系统瞬态响应的性能指标 V1-52 第三章控制系统的时域分析 2025/1/14

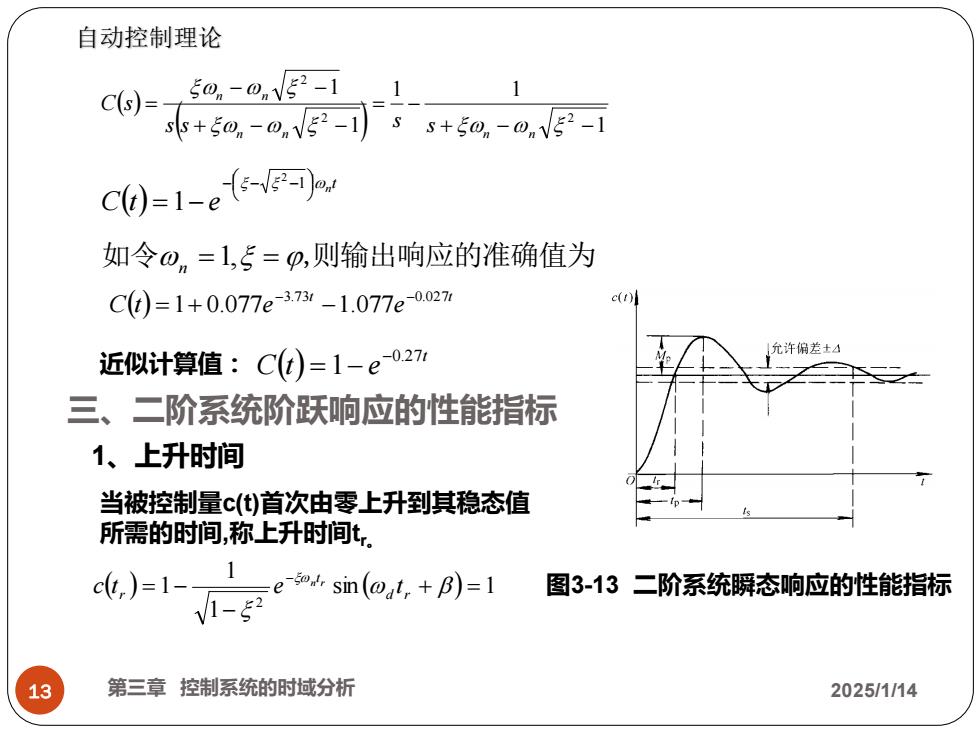
13 第三章 控制系统的时域分析 2025/1/14 自动控制理论 ( ) ( ) 1 1 1 1 1 2 2 2 + − − = − + − − − − =             n n n n n n s s s s C s ( ) t n C t e         − − − = − 1 2 1 如令n =1, = ,则输出响应的准确值为 ( ) t t C t e e 3.73 0.027 1 0.077 1.077 − − = + − ( ) t C t e 0.27 1 − 近似计算值： = − 三、二阶系统阶跃响应的性能指标 1、上升时间 当被控制量c(t)首次由零上升到其稳态值 所需的时间,称上升时间tr。 ( ) sin ( ) 1 图3-13 二阶系统瞬态响应的性能指标 1 1 1 2 + = − = − −     d r t r c t e t n r

自动控制理论 求得： 1=T-B Qa B=arctan 2、峰值时间 瞬态响应第一次出现峰值的时间叫峰值时间，用tp表示 =ea,+小e-0 E0,in@tp+B)=@jcosl@jtp+B) 1 a8 0atp=0、π2π. 14 第三章控制系统的时域分析 2025/1/14

14 第三章 控制系统的时域分析 2025/1/14       2 1 arctan − = − = d r t 自动控制理论 求得： 2、峰值时间 瞬态响应第一次出现峰值的时间叫峰值时间,用tp表示 ( )  sin ( ) cos( ) 0 1 1 − + + + = − = − − =           d p t d p n t t t n e t e t dt dc t n p n p p   ( +  ) =  ( +  ) n d p d d p in t cos t       0、 、2 1 1 tan = −  = d p t